 |
Visual Servoing Platform
version 3.6.1 under development (2025-02-18)
|
 |
Visual Servoing Platform
version 3.6.1 under development (2025-02-18)
|
#include <visp3/core/vpMatrix.h>
 Inheritance diagram for vpMatrix:
Inheritance diagram for vpMatrix:Public Types | |
| enum | vpDetMethod { LU_DECOMPOSITION } |
Public Member Functions | |
| vpMatrix () | |
| vpMatrix (unsigned int r, unsigned int c) | |
| vpMatrix (unsigned int r, unsigned int c, double val) | |
| vpMatrix (const vpMatrix &M, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) | |
| VP_EXPLICIT | vpMatrix (const vpArray2D< double > &A) |
| vpMatrix (const vpMatrix &A) | |
| VP_EXPLICIT | vpMatrix (const vpHomogeneousMatrix &R) |
| VP_EXPLICIT | vpMatrix (const vpRotationMatrix &R) |
| VP_EXPLICIT | vpMatrix (const vpVelocityTwistMatrix &V) |
| VP_EXPLICIT | vpMatrix (const vpForceTwistMatrix &F) |
| VP_EXPLICIT | vpMatrix (const vpColVector &v) |
| VP_EXPLICIT | vpMatrix (const vpRowVector &v) |
| VP_EXPLICIT | vpMatrix (const vpTranslationVector &t) |
| vpMatrix (vpMatrix &&A) | |
| VP_EXPLICIT | vpMatrix (const std::initializer_list< double > &list) |
| VP_EXPLICIT | vpMatrix (unsigned int nrows, unsigned int ncols, const std::initializer_list< double > &list) |
| VP_EXPLICIT | vpMatrix (const std::initializer_list< std::initializer_list< double > > &lists) |
| void | clear () |
Setting a diagonal matrix <br> | |
| void | diag (const double &val=1.0) |
| void | diag (const vpColVector &A) |
| void | eye () |
| void | eye (unsigned int n) |
| void | eye (unsigned int m, unsigned int n) |
Assignment operators | |
| vpMatrix & | operator<< (double *p) |
| vpMatrix & | operator<< (double val) |
| vpMatrix & | operator, (double val) |
| vpMatrix & | operator= (const vpArray2D< double > &A) |
| vpMatrix & | operator= (const vpMatrix &A) |
| vpMatrix & | operator= (const vpHomogeneousMatrix &M) |
| vpMatrix & | operator= (const vpRotationMatrix &R) |
| vpMatrix & | operator= (const vpVelocityTwistMatrix &V) |
| vpMatrix & | operator= (const vpForceTwistMatrix &F) |
| vpMatrix & | operator= (const vpColVector &v) |
| vpMatrix & | operator= (const vpRowVector &v) |
| vpMatrix & | operator= (const vpTranslationVector &t) |
| vpMatrix & | operator= (vpMatrix &&A) |
| vpMatrix & | operator= (const std::initializer_list< double > &list) |
| vpMatrix & | operator= (const std::initializer_list< std::initializer_list< double > > &lists) |
| vpMatrix & | operator= (double x) |
Stacking <br> | |
| void | stack (const vpMatrix &A) |
| void | stack (const vpRowVector &r) |
| void | stack (const vpColVector &c) |
| void | stackColumns (vpColVector &out) |
| vpColVector | stackColumns () |
| void | stackRows (vpRowVector &out) |
| vpRowVector | stackRows () |
Matrix insertion | |
| void | insert (const vpMatrix &A, unsigned int r, unsigned int c) |
Columns, rows, sub-matrices extraction | |
| vpMatrix | extract (unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) const |
| vpColVector | getCol (unsigned int j) const |
| vpColVector | getCol (unsigned int j, unsigned int i_begin, unsigned int size) const |
| vpRowVector | getRow (unsigned int i) const |
| vpRowVector | getRow (unsigned int i, unsigned int j_begin, unsigned int size) const |
| vpColVector | getDiag () const |
| void | init (const vpMatrix &M, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) |
Hadamard product <br> | |
| vpMatrix | hadamard (const vpMatrix &m) const |
Kronecker product <br> | |
| void | kron (const vpMatrix &m1, vpMatrix &out) const |
| vpMatrix | kron (const vpMatrix &m1) const |
Transpose <br> | |
| vpMatrix | t () const |
| vpMatrix | transpose () const |
| void | transpose (vpMatrix &At) const |
| vpMatrix | AAt () const |
| void | AAt (vpMatrix &B) const |
| vpMatrix | AtA () const |
| void | AtA (vpMatrix &B) const |
Matrix inversion <br> | |
| vpMatrix | inverseByLU () const |
| vpMatrix | inverseByLUEigen3 () const |
| vpMatrix | inverseByLULapack () const |
| vpMatrix | inverseByLUOpenCV () const |
| vpMatrix | inverseByCholesky () const |
| vpMatrix | inverseByCholeskyLapack () const |
| vpMatrix | inverseByCholeskyOpenCV () const |
| vpMatrix | inverseByQR () const |
| vpMatrix | inverseByQRLapack () const |
| vpMatrix | inverseTriangular (bool upper=true) const |
| vpMatrix | pseudoInverse (double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverse (int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseLapack (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseLapack (int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseEigen3 (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseEigen3 (int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseOpenCV (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseOpenCV (int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | dampedInverse (const double &ratioOfMaxSvd=1e-4) const |
SVD decomposition <br> | |
| double | cond (double svThreshold=1e-6) const |
| unsigned int | kernel (vpMatrix &kerAt, double svThreshold=1e-6) const |
| unsigned int | nullSpace (vpMatrix &kerA, double svThreshold=1e-6) const |
| unsigned int | nullSpace (vpMatrix &kerA, int dim) const |
| void | solveBySVD (const vpColVector &B, vpColVector &x) const |
| vpColVector | solveBySVD (const vpColVector &B) const |
| void | svd (vpColVector &w, vpMatrix &V) |
| void | svdEigen3 (vpColVector &w, vpMatrix &V) |
| void | svdLapack (vpColVector &w, vpMatrix &V) |
| void | svdOpenCV (vpColVector &w, vpMatrix &V) |
QR decomposition <br> | |
| unsigned int | qr (vpMatrix &Q, vpMatrix &R, bool full=false, bool squareR=false, double tol=1e-6) const |
| unsigned int | qrPivot (vpMatrix &Q, vpMatrix &R, vpMatrix &P, bool full=false, bool squareR=false, double tol=1e-6) const |
| void | solveByQR (const vpColVector &b, vpColVector &x) const |
| vpColVector | solveByQR (const vpColVector &b) const |
Eigen values <br> | |
| vpColVector | eigenValues () const |
| void | eigenValues (vpColVector &evalue, vpMatrix &evector) const |
Norms <br> | |
| double | frobeniusNorm () const |
| double | inducedL2Norm () const |
| double | infinityNorm () const |
Printing <br> | |
| std::ostream & | cppPrint (std::ostream &os, const std::string &matrixName="A", bool octet=false) const |
| std::ostream & | csvPrint (std::ostream &os) const |
| std::ostream & | maplePrint (std::ostream &os) const |
| std::ostream & | matlabPrint (std::ostream &os) const |
| int | print (std::ostream &s, unsigned int length, const std::string &intro="") const |
| void | printSize () const |
Inherited functionalities from vpArray2D | |
| unsigned int | getCols () const |
| double | getMaxValue () const |
| double | getMinValue () const |
| unsigned int | getRows () const |
| unsigned int | size () const |
| void | resize (unsigned int nrows, unsigned int ncols, bool flagNullify=true, bool recopy_=true) |
| void | reshape (unsigned int nrows, unsigned int ncols) |
| void | insert (const vpArray2D< double > &A, unsigned int r, unsigned int c) |
| bool | operator== (const vpArray2D< double > &A) const |
| bool | operator!= (const vpArray2D< double > &A) const |
| double * | operator[] (unsigned int i) |
| double * | operator[] (unsigned int i) const |
| vpArray2D< double > | hadamard (const vpArray2D< double > &m) const |
Static Public Member Functions | |
| static vpMatrix | view (double *data, unsigned int rows, unsigned int cols) |
| static vpArray2D< double > | view (const vpArray2D< double > &A) |
| static void | view (vpArray2D< double > &v, double *data, unsigned int numRows, unsigned int numCols) |
Linear algebra optimization <br> | |
| static unsigned int | getLapackMatrixMinSize () |
| static void | setLapackMatrixMinSize (unsigned int min_size) |
Setting a diagonal matrix with Static Public Member Functions <br> | |
| static void | createDiagonalMatrix (const vpColVector &A, vpMatrix &DA) |
Matrix insertion with Static Public Member Functions <br> | |
| static vpMatrix | insert (const vpMatrix &A, const vpMatrix &B, unsigned int r, unsigned int c) |
| static void | insert (const vpMatrix &A, const vpMatrix &B, vpMatrix &C, unsigned int r, unsigned int c) |
Stacking with Static Public Member Functions <br> | |
| static vpMatrix | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B) |
| static void | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static vpMatrix | stack (const vpMatrix &A, const vpMatrix &B) |
| static vpMatrix | stack (const vpMatrix &A, const vpRowVector &r) |
| static vpMatrix | stack (const vpMatrix &A, const vpColVector &c) |
| static void | stack (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | stack (const vpMatrix &A, const vpRowVector &r, vpMatrix &C) |
| static void | stack (const vpMatrix &A, const vpColVector &c, vpMatrix &C) |
Matrix operations with Static Public Member Functions <br> | |
| static void | add2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | add2Matrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
| static void | add2WeightedMatrices (const vpMatrix &A, const double &wA, const vpMatrix &B, const double &wB, vpMatrix &C) |
| static void | computeHLM (const vpMatrix &H, const double &alpha, vpMatrix &HLM) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpRotationMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpHomogeneousMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpColVector &B, vpColVector &C) |
| static void | multMatrixVector (const vpMatrix &A, const vpColVector &v, vpColVector &w) |
| static void | negateMatrix (const vpMatrix &A, vpMatrix &C) |
| static void | sub2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | sub2Matrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
Kronecker product with Static Public Member Functions <br> | |
| static void | kron (const vpMatrix &m1, const vpMatrix &m2, vpMatrix &out) |
| static vpMatrix | kron (const vpMatrix &m1, const vpMatrix &m2) |
Covariance computation with Static Public Member Functions <br> | |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b) |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b, const vpMatrix &w) |
| static vpMatrix | computeCovarianceMatrixVVS (const vpHomogeneousMatrix &cMo, const vpColVector &deltaS, const vpMatrix &Ls, const vpMatrix &W) |
| static vpMatrix | computeCovarianceMatrixVVS (const vpHomogeneousMatrix &cMo, const vpColVector &deltaS, const vpMatrix &Ls) |
Public Attributes | |
| double * | data |
Related Functions | |
(Note that these are not member functions.) | |
| void | insert (const vpMatrix &A, const vpMatrix &B, vpMatrix &C, unsigned int r, unsigned int c) |
| vpMatrix | operator* (const double &x, const vpMatrix &B) |
| enum | vpGEMMmethod |
| bool | operator== (const vpArray2D< double > &A) const |
| bool | operator== (const vpArray2D< float > &A) const |
| bool | operator!= (const vpArray2D< double > &A) const |
| void | vpGEMM (const vpArray2D< double > &A, const vpArray2D< double > &B, const double &alpha, const vpArray2D< double > &C, const double &beta, vpArray2D< double > &D, const unsigned int &ops=0) |
Matrix I/O with Static Public Member Functions <br> | |
| static bool | loadMatrix (const std::string &filename, vpArray2D< double > &M, bool binary=false, char *header=nullptr) |
| static bool | loadMatrixYAML (const std::string &filename, vpArray2D< double > &M, char *header=nullptr) |
| static bool | saveMatrix (const std::string &filename, const vpArray2D< double > &M, bool binary=false, const char *header="") |
| static bool | saveMatrixYAML (const std::string &filename, const vpArray2D< double > &M, const char *header="") |
Inherited I/O from vpArray2D with Static Public Member Functions | |
| vpArray2D< double > | insert (const vpArray2D< double > &A, const vpArray2D< double > &B, unsigned int r, unsigned int c) |
| static bool | load (const std::string &filename, vpArray2D< double > &A, bool binary=false, char *header=nullptr) |
| static bool | loadYAML (const std::string &filename, vpArray2D< double > &A, char *header=nullptr) |
| static bool | save (const std::string &filename, const vpArray2D< double > &A, bool binary=false, const char *header="") |
| static bool | saveYAML (const std::string &filename, const vpArray2D< double > &A, const char *header="") |
| static vpArray2D< double > | conv2 (const vpArray2D< double > &M, const vpArray2D< double > &kernel, const std::string &mode) |
| static void | conv2 (const vpArray2D< double > &M, const vpArray2D< double > &kernel, vpArray2D< double > &res, const std::string &mode) |
| static void | insert (const vpArray2D< double > &A, const vpArray2D< double > &B, vpArray2D< double > &C, unsigned int r, unsigned int c) |
| unsigned int | rowNum |
| unsigned int | colNum |
| double ** | rowPtrs |
| unsigned int | dsize |
| bool | isMemoryOwner |
| bool | isRowPtrsOwner |
Implementation of a matrix and operations on matrices.
This class needs one of the following third-party to compute matrix inverse, pseudo-inverse, singular value decomposition, determinant:
vpMatrix class provides a data structure for the matrices as well as a set of operations on these matrices.
The vpMatrix class is derived from vpArray2D<double>.
The code below shows how to create a 2-by-3 matrix of doubles, set the element values and access them:
Once build, this previous code produces the following output:
If ViSP is build with c++11 enabled, you can do the same using:
You can also create and initialize a matrix this way:
The Matrix could also be initialized using operator=(const std::initializer_list< std::initializer_list< double > > &)
Definition at line 168 of file vpMatrix.h.
Method used to compute the determinant of a square matrix.
| Enumerator | |
|---|---|
| LU_DECOMPOSITION | LU decomposition method. |
Definition at line 175 of file vpMatrix.h.
|
inline |
Basic constructor of a matrix of double. Number of columns and rows are zero.
Definition at line 185 of file vpMatrix.h.
Referenced by insert().
|
inline |
Constructor that initialize a matrix of double with 0.
| r | : Matrix number of rows. |
| c | : Matrix number of columns. |
Definition at line 193 of file vpMatrix.h.
|
inline |
Constructor that initialize a matrix of double with val.
| r | : Matrix number of rows. |
| c | : Matrix number of columns. |
| val | : Each element of the matrix is set to val. |
Definition at line 202 of file vpMatrix.h.
| vpMatrix::vpMatrix | ( | const vpMatrix & | M, |
| unsigned int | r, | ||
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) |
Construct a matrix as a sub-matrix of the input matrix M.
Definition at line 128 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, init(), and vpArray2D< Type >::rowNum.
|
inline |
Create a matrix from a 2D array that could be one of the following container that inherit from vpArray2D such as vpMatrix, vpRotationMatrix, vpHomogeneousMatrix, vpPoseVector, vpColVector, vpRowVector...
The following example shows how to create a matrix from an homogeneous matrix:
Definition at line 217 of file vpMatrix.h.
|
inline |
Definition at line 218 of file vpMatrix.h.
| vpMatrix::vpMatrix | ( | const vpHomogeneousMatrix & | M | ) |
Create a matrix from a homogeneous matrix.
| M | : Homogeneous matrix. |
Definition at line 146 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const vpRotationMatrix & | R | ) |
Create a matrix from a row vector.
| R | : Rotation matrix. |
Definition at line 173 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const vpVelocityTwistMatrix & | V | ) |
Create a matrix from a velocity twist matrix.
| V | : Velocity twist matrix. |
Definition at line 155 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const vpForceTwistMatrix & | F | ) |
Create a matrix from a force twist matrix.
| F | : Force twist matrix. |
Definition at line 164 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const vpColVector & | v | ) |
Create a matrix from a column vector.
| v | : Column vector. |
Definition at line 182 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const vpRowVector & | v | ) |
Create a matrix from a row vector.
| v | : Row vector. |
Definition at line 191 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const vpTranslationVector & | t | ) |
Create a matrix from a row vector.
| t | : Translation vector. |
Definition at line 200 of file vpMatrix.cpp.
References t().
| vpMatrix::vpMatrix | ( | vpMatrix && | A | ) |
Definition at line 206 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const std::initializer_list< double > & | list | ) |
Construct a matrix from a list of double values.
| list | : List of double. |
The following code shows how to use this constructor to initialize a 2-by-3 matrix using reshape() function:
It produces the following output:
Definition at line 236 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | unsigned int | nrows, |
| unsigned int | ncols, | ||
| const std::initializer_list< double > & | list | ||
| ) |
Construct a matrix from a list of double values.
| ncols,nrows | : Matrix size. |
| list | : List of double. |
The following code shows how to use this constructor to initialize a 2-by-3 matrix:
It produces the following output:
Definition at line 264 of file vpMatrix.cpp.
| vpMatrix::vpMatrix | ( | const std::initializer_list< std::initializer_list< double > > & | lists | ) |
Construct a matrix from a list of double values.
| lists | : List of double. The following code shows how to use this constructor to initialize a 2-by-3 matrix function: #include <visp3/core/vpMatrix.h>
#ifdef ENABLE_VISP_NAMESPACE
using namespace VISP_NAMESPACE_NAME;
#endif
int main()
{
vpMatrix M( { {-1, -2, -3}, {4, 5.5, 6} } );
std::cout << "M:\n" << M << std::endl;
}
M:
-1 -2 -3
4 5.5 6
|
Definition at line 292 of file vpMatrix.cpp.
| vpMatrix vpMatrix::AAt | ( | ) | const |
Computes the ![]() operation
operation ![]()
Definition at line 513 of file vpMatrix_operations.cpp.
Referenced by vpServo::computeControlLaw(), and vpServo::computeProjectionOperators().
| void vpMatrix::AAt | ( | vpMatrix & | B | ) | const |
Compute the AAt operation such as ![]() .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 533 of file vpMatrix_operations.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, vpArray2D< Type >::rowNum, and vpArray2D< double >::rowPtrs.
|
static |
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new vector won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 390 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 356 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator+().
|
static |
Operation C = A*wA + B*wB
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 324 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
| vpMatrix vpMatrix::AtA | ( | ) | const |
Compute the AtA operation such as ![]()
Definition at line 643 of file vpMatrix_operations.cpp.
Referenced by vpServo::computeProjectionOperators(), vpMbDepthDenseTracker::computeVVS(), vpMbDepthNormalTracker::computeVVS(), vpMbGenericTracker::computeVVS(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpRBDenseDepthTracker::computeVVSIter(), vpRBSilhouetteMeTracker::computeVVSIter(), vpTemplateTrackerWarpHomographySL3::findWarp(), and vpNurbs::globalCurveApprox().
| void vpMatrix::AtA | ( | vpMatrix & | B | ) | const |
Compute the AtA operation such as ![]() .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 591 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< Type >::rowNum.
| vpMatrix vpMatrix::cholesky | ( | ) | const |
Definition at line 1654 of file vpMatrix.cpp.
References choleskyByEigen3(), choleskyByLapack(), choleskyByOpenCV(), and vpException::fatalError.
Referenced by choleskyByLapack(), vpUKSigmaDrawerMerwe::drawSigmaPoints(), and inverseByCholeskyLapack().
| vpMatrix vpMatrix::choleskyByEigen3 | ( | ) | const |
Compute the Cholesky decomposition of a Hermitian positive-definite matrix using Eigen3 library.
Definition at line 372 of file vpMatrix_cholesky.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
Referenced by cholesky().
| vpMatrix vpMatrix::choleskyByLapack | ( | ) | const |
Compute the Cholesky decomposition of a Hermitian positive-definite matrix using Lapack library.
Definition at line 228 of file vpMatrix_cholesky.cpp.
References cholesky(), vpArray2D< double >::colNum, vpArray2D< Type >::data, vpMatrixException::forbiddenOperatorError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpMatrixException::matrixError, and vpArray2D< double >::rowNum.
Referenced by cholesky().
| vpMatrix vpMatrix::choleskyByOpenCV | ( | ) | const |
Compute the Cholesky decomposition of a Hermitian positive-definite matrix using OpenCV library.
Definition at line 342 of file vpMatrix_cholesky.cpp.
References vpArray2D< double >::colNum, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< double >::rowNum.
Referenced by cholesky().
|
inline |
Removes all elements from the matrix (which are destroyed), leaving the container with a size of 0.
Definition at line 240 of file vpMatrix.h.
|
static |
Compute the covariance matrix of the parameters x from a least squares minimization defined as: Ax = b
| A | : Matrix A from Ax = b. |
| x | : Vector x from Ax = b corresponding to the parameters to estimate. |
| b | : Vector b from Ax = b. |
Definition at line 55 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), pseudoInverse(), and t().
Referenced by computeCovarianceMatrixVVS(), and vpPose::poseVirtualVSrobust().
|
static |
Compute the covariance matrix of the parameters x from a least squares minimization defined as: WAx = Wb
| A | : Matrix A from WAx = Wb. |
| x | : Vector x from WAx = Wb corresponding to the parameters to estimate. |
| b | : Vector b from WAx = Wb. |
| W | : Diagonal weigths matrix from WAx = Wb. |
Definition at line 88 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpArray2D< Type >::getCols(), pseudoInverse(), and t().
|
static |
Compute the covariance matrix of an image-based virtual visual servoing. This assumes the optimization has been done via v = Ls.pseudoInverse() * DeltaS.
| cMo | : Pose matrix that has been computed with the v. |
| deltaS | : Error vector used in v = Ls.pseudoInverse() * DeltaS |
| Ls | : interaction matrix used in v = Ls.pseudoInverse() * DeltaS |
Definition at line 123 of file vpMatrix_covariance.cpp.
References computeCovarianceMatrix(), and computeCovarianceMatrixVVS().
|
static |
Compute the covariance matrix of an image-based virtual visual servoing. This assumes the optimization has been done via v = (W * Ls).pseudoInverse() W * DeltaS.
| cMo | : Pose matrix that has been computed with the v. |
| deltaS | : Error vector used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
| Ls | : interaction matrix used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
| W | : Weight matrix used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
Definition at line 148 of file vpMatrix_covariance.cpp.
References computeCovarianceMatrix().
Referenced by vpMbTracker::computeCovarianceMatrixVVS(), computeCovarianceMatrixVVS(), and vpPose::poseVirtualVS().
Compute ![]()
| H | : input Matrix 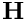 . This matrix should be square. . This matrix should be square. |
| alpha | : Scalar 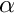 |
| HLM | : Resulting operation. |
Definition at line 1875 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
Referenced by vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerSSDESM::initCompInverse(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTrackerMIESM::initHessienDesired(), vpTemplateTrackerMIForwardAdditional::initHessienDesired(), vpTemplateTrackerMIForwardCompositional::initHessienDesired(), vpTemplateTrackerMIInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDESM::trackNoPyr(), vpTemplateTrackerSSDForwardAdditional::trackNoPyr(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), and vpTemplateTrackerMIInverseCompositional::trackNoPyr().
| double vpMatrix::cond | ( | double | svThreshold = 1e-6 | ) | const |
| svThreshold | Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Definition at line 1812 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), and svd().
Referenced by vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), and vpTemplateTrackerMIInverseCompositional::trackNoPyr().
|
staticinherited |
Perform a 2D convolution similar to Matlab conv2 function: ![]() .
.
| M | : First matrix. |
| kernel | : Second matrix. |
| mode | : Convolution mode: "full" (default), "same", "valid". |
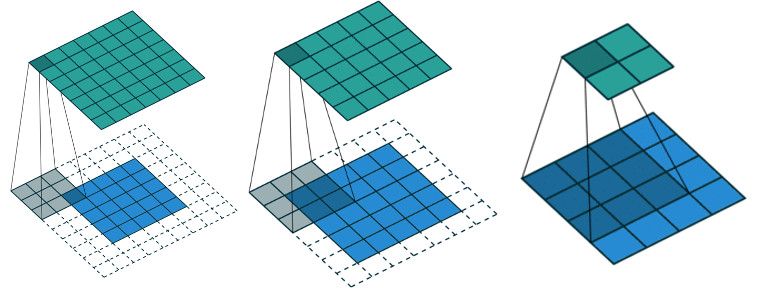
Definition at line 1138 of file vpArray2D.h.
|
staticinherited |
Perform a 2D convolution similar to Matlab conv2 function: ![]() .
.
| M | : First array. |
| kernel | : Second array. |
| res | : Result. |
| mode | : Convolution mode: "full" (default), "same", "valid". |

Definition at line 1152 of file vpArray2D.h.
|
static |
Perform a 2D convolution similar to Matlab conv2 function: ![]() .
.
| M | : First matrix. |
| kernel | : Second matrix. |
| mode | : Convolution mode: "full" (default), "same", "valid". |

Definition at line 905 of file vpMatrix_operations.cpp.
References kernel().
|
static |
Perform a 2D convolution similar to Matlab conv2 function: ![]() .
.
| M | : First array. |
| kernel | : Second array. |
| res | : Result. |
| mode | : Convolution mode: "full" (default), "same", "valid". |

Definition at line 912 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::data, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), kernel(), and vpArray2D< Type >::resize().
| std::ostream & vpMatrix::cppPrint | ( | std::ostream & | os, |
| const std::string & | matrixName = "A", |
||
| bool | octet = false |
||
| ) | const |
Print to be used as part of a C++ code later.
| os | : the stream to be printed in. |
| matrixName | : name of the matrix, "A" by default. |
| octet | : if false, print using double, if true, print byte per byte each bytes of the double array. |
The following code shows how to use this function:
It produces the following output that could be copy/paste in a C++ code:
Definition at line 1106 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
|
static |
Create a diagonal matrix with the element of a vector ![]() .
.
| A | : Vector which element will be put in the diagonal. |
| DA | : Diagonal matrix DA[i][i] = A[i] |
Definition at line 755 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
| std::ostream & vpMatrix::csvPrint | ( | std::ostream & | os | ) | const |
Print/save a matrix in csv format.
The following code
produces log.csv file that contains:
Definition at line 1051 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
| vpMatrix vpMatrix::dampedInverse | ( | const double & | ratioOfMaxSvd = 1e-4 | ) | const |
Permits to compute an approximated inverse of a matrix that is ill-conditionned. If the matrix is well-conditionned, the damped inverse is close to the Moore-Penrose pseudo-inverse.
The corresponding equation is the following, assuming that ![]() is the matrix we want to compute the damped inverse:
is the matrix we want to compute the damped inverse:
![]()
| [in] | ratioOfMaxSvd | The ratio of the maximum singular value of |
Definition at line 1025 of file vpMatrix_pseudo_inverse.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::getMaxValue(), inverseByLU(), svd(), and transpose().
| double vpMatrix::det | ( | vpDetMethod | method = LU_DECOMPOSITION | ) | const |
Compute the determinant of a n-by-n matrix.
| method | : Method used to compute the determinant. Default LU decomposition method is faster than the method based on Gaussian elimination. |
Definition at line 1643 of file vpMatrix.cpp.
References detByLU(), and LU_DECOMPOSITION.
Referenced by vpHomogeneousMatrix::compute3d3dTransformation(), detByLULapack(), detByLUOpenCV(), vpTemplateTrackerTriangle::init(), inverseByLU(), and vpRotationMatrix::orthogonalize().
| double vpMatrix::detByLU | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition.
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default detByLULapack() with a Lapack built-in version.
Definition at line 236 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, detByLUEigen3(), detByLULapack(), detByLUOpenCV(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by det().
| double vpMatrix::detByLUEigen3 | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition with Eigen3 3rd party.
Definition at line 656 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< double >::rowNum.
Referenced by detByLU().
| double vpMatrix::detByLULapack | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition with Lapack 3rd party.
Definition at line 404 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, det(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by detByLU().
| double vpMatrix::detByLUOpenCV | ( | ) | const |
Compute the determinant of a n-by-n matrix using the LU decomposition with OpenCV 3rd party.
Definition at line 558 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, det(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by detByLU().
| void vpMatrix::diag | ( | const double & | val = 1.0 | ) |
Set the matrix as a diagonal matrix where each element on the diagonal is set to val. Elements that are not on the diagonal are set to 0.
| val | : Value to set. |
Matrix A is now equal to:
Definition at line 736 of file vpMatrix_operations.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by getDiag().
| void vpMatrix::diag | ( | const vpColVector & | A | ) |
Create a diagonal matrix with the element of a vector.
| A | : Vector which element will be put in the diagonal. |
Matrix A is now equal to:
Definition at line 691 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpColVector vpMatrix::eigenValues | ( | ) | const |
Compute the eigenvalues of a n-by-n real symmetric matrix using Lapack 3rd party.
| vpException::dimensionError | If the matrix is not square. |
| vpException::fatalError | If the matrix is not symmetric. |
| vpException::functionNotImplementedError | If the Lapack 3rd party is not detected. |
Here an example:
Definition at line 1198 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpException::functionNotImplementedError, vpColVector::resize(), vpArray2D< double >::rowNum, and t().
Referenced by vpQuadProg::fromCanonicalCost(), and vpMath::lineFitting().
| void vpMatrix::eigenValues | ( | vpColVector & | evalue, |
| vpMatrix & | evector | ||
| ) | const |
Compute the eigenvalues of a n-by-n real symmetric matrix using Lapack 3rd party.
| evalue | : Eigenvalues of the matrix, sorted in ascending order. |
| evector | : Corresponding eigenvectors of the matrix. |
| vpException::dimensionError | If the matrix is not square. |
| vpException::fatalError | If the matrix is not symmetric. |
| vpException::functionNotImplementedError | If Lapack 3rd party is not detected. |
Here an example:
Definition at line 1321 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpException::functionNotImplementedError, vpColVector::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and t().
| vpMatrix vpMatrix::expm | ( | ) | const |
Compute the exponential matrix of a square matrix.
Definition at line 1675 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, eye(), inverseByLU(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and sum().
Referenced by vpTemplateTrackerWarpHomographySL3::computeCoeff().
| vpMatrix vpMatrix::extract | ( | unsigned int | r, |
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) | const |
Extract a sub matrix from a matrix M.
| r | : row index in matrix M. |
| c | : column index in matrix M. |
| nrows | : Number of rows of the matrix that should be extracted. |
| ncols | : Number of columns of the matrix that should be extracted. |
The following code shows how to use this function:
It produces the following output:
Definition at line 430 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< Type >::resize().
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
| void vpMatrix::eye | ( | ) |
Set an m-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 786 of file vpMatrix_operations.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpServo::computeControlLaw(), vpMbDepthDenseTracker::computeVVS(), vpMbDepthNormalTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpMbGenericTracker::computeVVS(), vpMbTracker::computeVVSPoseEstimation(), expm(), eye(), vpTemplateTrackerWarpHomographySL3::getdW0(), vpTemplateTrackerWarpHomographySL3::getdWdp0(), vpFeatureThetaU::interaction(), vpPose::poseFromRectangle(), vpRobotKinova::setCartVelocity(), vpServo::setServo(), vpLinProg::solveLP(), vpRBTracker::track(), vpMbTracker::vpMbTracker(), and vpServo::vpServo().
| void vpMatrix::eye | ( | unsigned int | m, |
| unsigned int | n | ||
| ) |
Set an m-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 775 of file vpMatrix_operations.cpp.
References eye(), and vpArray2D< double >::resize().
| void vpMatrix::eye | ( | unsigned int | n | ) |
Set an n-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 769 of file vpMatrix_operations.cpp.
References eye().
| double vpMatrix::frobeniusNorm | ( | ) | const |
Compute and return the Frobenius norm (also called Euclidean norm) ![]() .
.
Definition at line 1896 of file vpMatrix.cpp.
References vpArray2D< double >::data, and vpArray2D< double >::dsize.
| vpColVector vpMatrix::getCol | ( | unsigned int | j | ) | const |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If j=0, the first column is extracted. |
The following example shows how to use this function:
It produces the following output :
Definition at line 554 of file vpMatrix.cpp.
References vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpHomography::DLT(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), kernel(), vpLuminancePCA::learn(), vpPose::poseFromRectangle(), vpServo::secondaryTaskJointLimitAvoidance(), and vpLinProg::simplex().
| vpColVector vpMatrix::getCol | ( | unsigned int | j, |
| unsigned int | i_begin, | ||
| unsigned int | column_size | ||
| ) | const |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If col=0, the first column is extracted. |
| i_begin | : Index of the row that gives the location of the first element of the column vector to extract. |
| column_size | : Size of the column vector to extract. |
The following example shows how to use this function:
It produces the following output :
Definition at line 498 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
|
inlineinherited |
Return the number of columns of the 2D array.
Definition at line 417 of file vpArray2D.h.
| vpColVector vpMatrix::getDiag | ( | ) | const |
Extract a diagonal vector from a matrix.
The following example shows how to use this function:
It produces the following output :
Definition at line 693 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, diag(), and vpArray2D< double >::rowNum.
|
inlinestatic |
Return the minimum size of rows and columns required to enable Blas/Lapack usage on matrices and vectors.
To get more info see Tutorial: Basic linear algebra operations.
Definition at line 269 of file vpMatrix.h.
|
inherited |
Return the array max value.
Definition at line 419 of file vpArray2D.h.
|
inherited |
Return the array min value.
Definition at line 421 of file vpArray2D.h.
| vpRowVector vpMatrix::getRow | ( | unsigned int | i | ) | const |
Extract a row vector from a matrix.
| i | : Index of the row to extract. If i=0, the first row is extracted. |
The following example shows how to use this function:
It produces the following output :
Definition at line 596 of file vpMatrix.cpp.
References vpArray2D< double >::colNum.
Referenced by vpLinProg::allClose(), vpLinProg::allLesser(), vpUKSigmaDrawerMerwe::drawSigmaPoints(), vpLinProg::solveLP(), and vpQuadProg::solveQPi().
| vpRowVector vpMatrix::getRow | ( | unsigned int | i, |
| unsigned int | j_begin, | ||
| unsigned int | row_size | ||
| ) | const |
Extract a row vector from a matrix.
| i | : Index of the row to extract.If i = 0, the first row is extracted. |
| j_begin | : Index of the column that gives the location of the first element of the row vector to extract. |
| row_size | : Size of the row vector to extract. |
The following example shows how to use this function:
It produces the following output :
Definition at line 641 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, and vpArray2D< double >::rowNum.
|
inlineinherited |
Return the number of rows of the 2D array.
Definition at line 427 of file vpArray2D.h.
Compute the Hadamard product (element wise matrix multiplication).
| m | : Second matrix; |
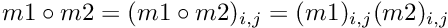
Definition at line 726 of file vpArray2D.h.
Compute the Hadamard product (element wise matrix multiplication).
| m | : Second matrix; |
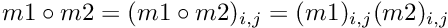
Definition at line 806 of file vpMatrix_operations.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
| double vpMatrix::inducedL2Norm | ( | ) | const |
Compute and return the induced L2 norm ![]() which is equal to the maximum singular value of the matrix.
which is equal to the maximum singular value of the matrix.
Definition at line 1915 of file vpMatrix.cpp.
References vpArray2D< double >::dsize, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::size(), and svd().
| double vpMatrix::infinityNorm | ( | ) | const |
Compute and return the infinity norm ![]() with
with ![]() where
where ![]() is the matrix size.
is the matrix size.
Definition at line 1956 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by vpLinProg::colReduction(), and vpLinProg::rowReduction().
| void vpMatrix::init | ( | const vpMatrix & | M, |
| unsigned int | r, | ||
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) |
Initialize the matrix from a part of an input matrix M.
| M | : Input matrix used for initialization. |
| r | : row index in matrix M. |
| c | : column index in matrix M. |
| nrows | : Number of rows of the matrix that should be initialized. |
| ncols | : Number of columns of the matrix that should be initialized. |
The sub-matrix starting from M[r][c] element and ending on M[r+nrows-1][c+ncols-1] element is used to initialize the matrix.
The following code shows how to use this function:
It produces the following output:
Definition at line 363 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
Referenced by vpMatrix().
|
inherited |
Insert array B in array A at the given position.
| A | : Main array. |
| B | : Array to insert. |
| r | : Index of the row where to add the array. |
| c | : Index of the column where to add the array. |
Definition at line 1166 of file vpArray2D.h.
|
inlineinherited |
Insert array A at the given position in the current array.
| A | : The array to insert. |
| r | : The index of the row to begin to insert data. |
| c | : The index of the column to begin to insert data. |
Definition at line 580 of file vpArray2D.h.
|
static |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| r | : Index of the row where to add the matrix. |
| c | : Index of the column where to add the matrix. |
Definition at line 721 of file vpMatrix.cpp.
References vpArray2D< Type >::insert(), and vpMatrix().
|
static |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| C | : Result matrix. |
| r | : Index of the row where to insert matrix B. |
| c | : Index of the column where to insert matrix B. |
Definition at line 743 of file vpMatrix.cpp.
References vpArray2D< Type >::insert().
| void vpMatrix::insert | ( | const vpMatrix & | A, |
| unsigned int | r, | ||
| unsigned int | c | ||
| ) |
Insert matrix A at the given position in the current matrix.
| A | : The matrix to insert. |
| r | : The index of the row to begin to insert data. |
| c | : The index of the column to begin to insert data. |
Definition at line 1139 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, and vpArray2D< Type >::size().
Referenced by vpMbDepthDenseTracker::computeVVSInteractionMatrixAndResidu(), vpMbDepthNormalTracker::computeVVSInteractionMatrixAndResidu(), vpMbGenericTracker::computeVVSInteractionMatrixAndResidu(), cond(), conv2(), vpNurbs::curveKnotIns(), juxtaposeMatrices(), kernel(), nullSpace(), vpRobotKinova::setCartVelocity(), and stack().
| BEGIN_VISP_NAMESPACE vpMatrix vpMatrix::inverseByCholesky | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition. The matrix must be real symmetric positive defined.
This function calls the first following function that is available:
If none of these 3rd parties is installed we use a Lapack built-in version.
Here an example:
Definition at line 112 of file vpMatrix_cholesky.cpp.
References vpException::fatalError, inverseByCholeskyLapack(), and inverseByCholeskyOpenCV().
Referenced by vpRBSilhouetteCCDTracker::computeErrorAndInteractionMatrix(), and vpUnscentedKalman::update().
| vpMatrix vpMatrix::inverseByCholeskyLapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition with Lapack 3rd party. The matrix must be real symmetric positive defined.
Here an example:
Definition at line 164 of file vpMatrix_cholesky.cpp.
References vpException::badValue, cholesky(), vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::fatalError, vpArray2D< Type >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::getRows(), vpMatrixException::matrixError, and vpArray2D< double >::rowNum.
Referenced by inverseByCholesky().
| vpMatrix vpMatrix::inverseByCholeskyOpenCV | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition with OpenCV 3rd party. The matrix must be real symmetric positive defined.
Here an example:
Definition at line 320 of file vpMatrix_cholesky.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByCholesky().
| BEGIN_VISP_NAMESPACE vpMatrix vpMatrix::inverseByLU | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition.
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default inverseByLULapack() with a Lapack built-in version.
Here an example:
Definition at line 130 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, det(), vpException::fatalError, inverseByLUEigen3(), inverseByLULapack(), inverseByLUOpenCV(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
Referenced by dampedInverse(), expm(), vpKalmanFilter::filtering(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerTriangle::init(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTrackerMIESM::initHessienDesired(), vpTemplateTrackerMIForwardAdditional::initHessienDesired(), vpTemplateTrackerMIForwardCompositional::initHessienDesired(), vpTemplateTrackerMIInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDForwardAdditional::trackNoPyr(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), vpTemplateTrackerMIInverseCompositional::trackNoPyr(), and vpImageTools::warpImage().
| vpMatrix vpMatrix::inverseByLUEigen3 | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with Eigen3 3rd party.
Here an example:
Definition at line 610 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByLULapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with Lapack 3rd party.
Here an example:
Definition at line 303 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByLUOpenCV | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with OpenCV 3rd party.
Here an example:
Definition at line 513 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByQR | ( | ) | const |
Compute the inverse of a n-by-n matrix using the QR decomposition. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
Here an example:
Definition at line 382 of file vpMatrix_qr.cpp.
References vpException::fatalError, and inverseByQRLapack().
Referenced by vpLinProg::simplex().
| BEGIN_VISP_NAMESPACE vpMatrix vpMatrix::inverseByQRLapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the QR decomposition with Lapack 3rd party.
Here an example:
Definition at line 148 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::getRows(), vpMatrixException::matrixError, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by inverseByQR().
| vpMatrix vpMatrix::inverseTriangular | ( | bool | upper = true | ) | const |
Compute the inverse of a full-rank n-by-n triangular matrix. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| upper | : if it is an upper triangular matrix |
The function does not check if the matrix is actually upper or lower triangular.
Definition at line 1172 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpMatrixException::rankDeficient, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
Juxtapose to matrices C = [ A B ].
![]()
| A | : Left matrix. |
| B | : Right matrix. |
Definition at line 763 of file vpMatrix.cpp.
Referenced by vpLinProg::colReduction().
Juxtapose to matrices C = [ A B ].
![]()
| A | : Left matrix. |
| B | : Right matrix. |
| C | : Juxtaposed matrix C = [ A B ] |
Definition at line 784 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), and vpArray2D< Type >::resize().
| unsigned int vpMatrix::kernel | ( | vpMatrix & | kerAt, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix ![]() .
.
The null space of a matrix ![]() is defined as
is defined as ![]() .
.
| kerAt | The matrix that contains the null space (kernel) of kerAt is (0, n), otherwise the dimension is (n-r, n). This matrix is thus the transpose of |
| svThreshold | Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Definition at line 1418 of file vpMatrix.cpp.
References getCol(), vpArray2D< double >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), vpColVector::sumSquare(), and svd().
Referenced by conv2().
Compute Kronecker product matrix.
| m | : vpMatrix; |
Definition at line 903 of file vpMatrix_operations.cpp.
References kron().
Compute Kronecker product matrix.
Definition at line 871 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
Compute Kronecker product matrix.
Definition at line 832 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
Compute Kronecker product matrix.
| m | : vpMatrix. |
| out | : If m1.kron(m2) out contains the kronecker product's result : |
Definition at line 863 of file vpMatrix_operations.cpp.
Referenced by kron().
|
inlinestaticinherited |
Load a matrix from a file.
| filename | : Absolute file name. |
| A | : Array to be loaded |
| binary | : If true the matrix is loaded from a binary file, else from a text file. |
| header | : Header of the file is loaded in this parameter. |
Definition at line 754 of file vpArray2D.h.
|
inlinestatic |
Load a matrix from a file. This function overloads vpArray2D::load().
| filename | : Absolute file name. |
| M | : Matrix to be loaded. |
| binary | : If true the matrix data are considered as binary, otherwise as human readable (text) data. Using binary data allows to keep data precision. |
| header | : Header of the file is loaded in this parameter. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.bin file where data are saved as binary data is the following:
% cat matrix.bin My header??@@@%
Definition at line 831 of file vpMatrix.h.
References vpArray2D< Type >::load().
Referenced by vpDot2::defineDots(), and vpLuminancePCA::load().
|
inlinestatic |
Load a matrix from a YAML-formatted file. This function overloads vpArray2D::loadYAML().
| filename | : Absolute YAML file name. |
| M | : Matrix to be loaded from the file. |
| header | : Header of the file is loaded in this parameter. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.yaml file is the following:
% cat matrix.yaml My header rows: 2 cols: 3 data: - [-1, -2, -3] - [4, 5.5, 6]
Definition at line 910 of file vpMatrix.h.
References vpArray2D< Type >::loadYAML().
|
inlinestaticinherited |
Load an array from a YAML-formatted file.
| filename | : absolute file name. |
| A | : array to be loaded from the file. |
| header | : header of the file is loaded in this parameter. |
Definition at line 868 of file vpArray2D.h.
| std::ostream & vpMatrix::maplePrint | ( | std::ostream & | os | ) | const |
Print using Maple syntax, to copy/paste in Maple later.
The following code
produces this output:
that could be copy/paste in Maple.
Definition at line 1004 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
| std::ostream & vpMatrix::matlabPrint | ( | std::ostream & | os | ) | const |
Print using Matlab syntax, to copy/paste in Matlab later.
The following code
produces this output:
that could be copy/paste in Matlab:
Definition at line 953 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 309 of file vpMatrix_operations.cpp.
References multMatrixVector().
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If matrices are not 4-by-4 dimension. |
Definition at line 249 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 153 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator*().
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If matrices are not 3-by-3 dimension. |
Definition at line 211 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
|
static |
Operation w = A * v (v and w are vectors).
A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 102 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by mult2Matrices(), and operator*().
Operation C = -A.
The result is placed in the second parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 492 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator-().
| unsigned int vpMatrix::nullSpace | ( | vpMatrix & | kerA, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix ![]() .
.
The null space of a matrix ![]() is defined as
is defined as ![]() .
.
| kerA | The matrix that contains the null space (kernel) of kerA is (n, 0), otherwise its dimension is (n, n-r). |
| svThreshold | Threshold used to test the singular values. The dimension of kerA corresponds to the number of singular values lower than this threshold |
Definition at line 1493 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), and svd().
Referenced by vpMeLine::leastSquare(), vpMeEllipse::leastSquare(), and vpMeEllipse::leastSquareRobustEllipse().
| unsigned int vpMatrix::nullSpace | ( | vpMatrix & | kerA, |
| int | dim | ||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix ![]() .
.
The null space of a matrix ![]() is defined as
is defined as ![]() .
.
| kerA | The matrix that contains the null space (kernel) of kerA is (n, 0), otherwise its dimension is (n, n-r). |
| dim | the dimension of the null space when it is known a priori |
Definition at line 1561 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), and svd().
|
inherited |
Not equal to comparison operator of a 2D array.
Definition at line 606 of file vpArray2D.h.
| vpColVector vpMatrix::operator* | ( | const vpColVector & | v | ) | const |
Operation w = A * v (matrix A is unchanged, v and w are column vectors).
Definition at line 403 of file vpMatrix_operators.cpp.
References multMatrixVector().
| vpMatrix vpMatrix::operator* | ( | const vpForceTwistMatrix & | V | ) | const |
Operator that allow to multiply a matrix by a force/torque twist matrix. The matrix should be of dimension m-by-6.
Definition at line 547 of file vpMatrix_operators.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | const vpHomogeneousMatrix & | M | ) | const |
Operator that allow to multiply a matrix by a homogeneous matrix. The matrix should be of dimension m-by-4.
Definition at line 458 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Operation C = A * B (A is unchanged).
Definition at line 414 of file vpMatrix_operators.cpp.
References mult2Matrices().
| vpMatrix vpMatrix::operator* | ( | const vpRotationMatrix & | R | ) | const |
Operator that allow to multiply a matrix by a rotation matrix. The matrix should be of dimension m-by-3.
Definition at line 427 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpTranslationVector vpMatrix::operator* | ( | const vpTranslationVector & | tv | ) | const |
Operator that allows to multiply a matrix by a translation vector. The matrix should be of dimension (3x3)
Definition at line 376 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | const vpVelocityTwistMatrix & | V | ) | const |
Operator that allow to multiply a matrix by a velocity twist matrix. The matrix should be of dimension m-by-6.
Definition at line 490 of file vpMatrix_operators.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | double | x | ) | const |
Operator that allows to multiply all the elements of a matrix by a scalar.
Definition at line 687 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator*= | ( | double | x | ) |
Multiply all the element of the matrix by x : Aij = Aij * x.
Operator that allows to multiply all the elements of a matrix by a scalar.
Definition at line 759 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Operation C = A + B (A is unchanged).
Definition at line 604 of file vpMatrix_operators.cpp.
References add2Matrices().
Operation A = A + B.
Definition at line 624 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, vpArray2D< double >::rowPtrs, and vpArray2D< Type >::rowPtrs.
| vpMatrix & vpMatrix::operator+= | ( | double | x | ) |
Add x to all the element of the matrix : Aij = Aij + x.
Definition at line 732 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator, | ( | double | val | ) |
Definition at line 365 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator- | ( | void | ) | const |
Operation C = -A (A is unchanged).
Definition at line 664 of file vpMatrix_operators.cpp.
References negateMatrix().
Operation C = A - B (A is unchanged).
Definition at line 615 of file vpMatrix_operators.cpp.
References sub2Matrices().
Operation A = A - B.
Definition at line 643 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, vpArray2D< double >::rowPtrs, and vpArray2D< Type >::rowPtrs.
| vpMatrix & vpMatrix::operator-= | ( | double | x | ) |
subtract x to all the element of the matrix : Aij = Aij - x
Definition at line 744 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator/ | ( | double | x | ) | const |
Cij = Aij / x (A is unchanged)
Definition at line 707 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpException::divideByZeroError, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator/= | ( | double | x | ) |
Divide all the element of the matrix by x : Aij = Aij / x.
Definition at line 775 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpException::divideByZeroError, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator<< | ( | double * | x | ) |
Assignment from an array of double. This method has to be used carefully since the array allocated behind x pointer should have the same dimension than the matrix.
Definition at line 348 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator<< | ( | double | val | ) |
Definition at line 358 of file vpMatrix_operators.cpp.
References vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator= | ( | const std::initializer_list< double > & | list | ) |
Set matrix elements from a list of values.
| list | : List of double. Matrix size (number of columns multiplied by number of columns) should match the number of elements. |
It produces the following printings:
Definition at line 279 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< double >::dsize, and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const std::initializer_list< std::initializer_list< double > > & | lists | ) |
Set matrix elements from a list of values.
| lists | : List of double. |
Definition at line 317 of file vpMatrix_operators.cpp.
References vpArray2D< double >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Copy operator that allows to convert on of the following container that inherit from vpArray2D such as vpMatrix, vpRotationMatrix, vpHomogeneousMatrix, vpPoseVector, vpColVector, vpRowVector... into a vpMatrix.
| A | : 2D array to be copied. |
The following example shows how to create a matrix from an homogeneous matrix:
Definition at line 59 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const vpColVector & | v | ) |
Copy operator that allows to convert a column vector to a matrix.
| v | : Column vector. |
The following example shows how to create a matrix from a column vector:
Definition at line 174 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const vpForceTwistMatrix & | F | ) |
Copy operator that allows to convert a force twist matrix to a matrix.
| F | : Force twist matrix. |
The following example shows how to create a matrix from a force twist matrix:
Definition at line 151 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const vpHomogeneousMatrix & | M | ) |
Copy operator that allows to convert a homogenous matrix to a matrix.
| M | : Homogeneous matrix. |
The following example shows how to create a matrix from a homogenous matrix:
Definition at line 82 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
Definition at line 231 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const vpRotationMatrix & | R | ) |
Copy operator that allows to convert a rotation matrix to a matrix.
| R | : Rotation matrix. |
The following example shows how to create a matrix from a rotation matrix:
Definition at line 105 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const vpRowVector & | v | ) |
Copy operator that allows to convert a row vector to a matrix.
| v | : Column vector. |
The following example shows how to create a matrix from a row vector:
Definition at line 197 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const vpTranslationVector & | t | ) |
Copy operator that allows to convert a translation vector to a matrix.
| t | : Translation vector. |
The following example shows how to create a matrix from a translation vector:
Definition at line 220 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::resize(), and t().
| vpMatrix & vpMatrix::operator= | ( | const vpVelocityTwistMatrix & | V | ) |
Copy operator that allows to convert a velocity twist matrix to a matrix.
| V | : Velocity twist matrix. |
The following example shows how to create a matrix from a velocity twist matrix:
Definition at line 128 of file vpMatrix_operators.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | double | x | ) |
Set all the element of the matrix A to x.
Definition at line 337 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, and vpArray2D< double >::rowNum.
Definition at line 243 of file vpMatrix_operators.cpp.
References vpArray2D< Type >::operator=().
Equal to comparison operator of a 2D array.
Definition at line 602 of file vpArray2D.h.
|
inlineinherited |
Set element 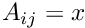 using A[i][j] = x.
using A[i][j] = x.
Definition at line 690 of file vpArray2D.h.
|
inlineinherited |
Get element 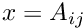 using x = A[i][j].
using x = A[i][j].
Definition at line 692 of file vpArray2D.h.
| int vpMatrix::print | ( | std::ostream & | s, |
| unsigned int | length, | ||
| const std::string & | intro = "" |
||
| ) | const |
Pretty print a matrix. The data are tabulated. The common widths before and after the decimal point are set with respect to the parameter length.
| s | : Stream used for the printing. |
| length | : The suggested width of each matrix element. If needed, the used length grows in order to accommodate the whole integral part, and shrinks the decimal part to print only length digits. |
| intro | : The introduction which is printed before the matrix. Can be set to zero (or omitted), in which case the introduction is not printed. |
Definition at line 830 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpMath::maximum(), and vpArray2D< double >::size().
Referenced by vpServo::computeControlLaw().
|
inline |
Definition at line 663 of file vpMatrix.h.
References vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
| vpMatrix vpMatrix::pseudoInverse | ( | double | svThreshold = 1e-6 | ) | const |
Compute and return the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() .
.
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 332 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
Referenced by vpServo::computeControlLaw(), computeCovarianceMatrix(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpMbTracker::computeVVSPoseEstimation(), vpQuadProg::fromCanonicalCost(), vpRBTracker::getCovariance(), vpNurbs::globalCurveApprox(), vpNurbs::globalCurveInterp(), vpHomography::inverse(), vpHomogeneousMatrix::mean(), vpRotationMatrix::mean(), vpPose::poseDementhonNonPlan(), vpPose::poseDementhonPlan(), vpPose::poseFromRectangle(), pseudoInverse(), vpHomography::robust(), solveBySVD(), and vpQuadProg::solveQPi().
| vpMatrix vpMatrix::pseudoInverse | ( | int | rank_in | ) | const |
Compute and return the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() .
.
| [in] | rank_in | : Known rank of the matrix. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 401 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| BEGIN_VISP_NAMESPACE unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 182 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse | |
| [in] | rank_in | : Known rank of the matrix. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 262 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
See pseudoInverse(vpMatrix &, vpColVector &, double, vpMatrix &, vpMatrix &, vpMatrix &) const for a complete description of this function.
| Ap | : The Moore-Penros pseudo inverse |
| sv | Vector corresponding to matrix |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
| imA | |
| imAt |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 662 of file vpMatrix_pseudo_inverse.cpp.
References pseudoInverse().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() ,
, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse |
| sv | : Vector corresponding to matrix A singular values. The size of this vector is equal to min(m, n). |
| svThreshold | : Threshold used to test the singular values.If a singular value is lower than this threshold we consider that the matrix is not full rank. |
| imA | : |
| imAt | : |
| kerAt | : The matrix that contains the null space(kernel) of kerAt is(0, n), otherwise the dimension is (n - r, n). This matrix is thus the transpose of |
Here an example to compute the pseudo - inverse of a 2 - by - 3 matrix that is rank 2.
Once build, the previous example produces the following output :
Definition at line 861 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values and return the rank of the matrix.
along with singular values and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse |
| sv | Vector corresponding to matrix |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 481 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values and return the rank of the matrix.
along with singular values and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse | |
| sv | Vector corresponding to matrix | |
| [in] | rank_in | : Known rank of the matrix. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 568 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
See pseudoInverse(vpMatrix &, vpColVector &, double, vpMatrix &, vpMatrix &, vpMatrix &) const for a complete description of this function.
| Ap | : The Moore-Penros pseudo inverse | |
| sv | Vector corresponding to matrix | |
| [in] | rank_in | : Known rank of the matrix. |
| imA | ||
| imAt |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 750 of file vpMatrix_pseudo_inverse.cpp.
References pseudoInverse().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() ,
, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore - Penros pseudo inverse | |
| sv | : Vector corresponding to matrix | |
| [in] | rank_in | : Known rank of the matrix. |
| imA | : | |
| imAt | : | |
| kerAt | : The matrix that contains the null space(kernel) of kerAt is(0, n), otherwise the dimension is(n - r, n).This matrix is thus the transpose of |
Here an example to compute the pseudo - inverse of a 2 - by - 3 matrix that is rank 2.
Once build, the previous example produces the following output :
Definition at line 992 of file vpMatrix_pseudo_inverse.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| vpMatrix vpMatrix::pseudoInverseEigen3 | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| vpMatrix vpMatrix::pseudoInverseEigen3 | ( | int | rank_in | ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseLapack | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| vpMatrix vpMatrix::pseudoInverseLapack | ( | int | rank_in | ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseOpenCV | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| vpMatrix vpMatrix::pseudoInverseOpenCV | ( | int | rank_in | ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::qr | ( | vpMatrix & | Q, |
| vpMatrix & | R, | ||
| bool | full = false, |
||
| bool | squareR = false, |
||
| double | tol = 1e-6 |
||
| ) | const |
Compute the QR decomposition of a (m x n) matrix of rank r. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| Q | : orthogonal matrix (will be modified). |
| R | : upper-triangular matrix (will be modified). |
| full | : whether or not we want full decomposition. |
| squareR | : will return only the square (min(m,n) x min(m,n)) part of R. |
| tol | : tolerance to test the rank of R. |
If full is false (default) then Q is (m x min(n,m)) and R is (min(n,m) x n). We then have this = QR.
If full is true and m > n then Q is (m x m) and R is (n x n). In this case this = Q (R, 0)^T
If squareR is true and n > m then R is (m x m). If r = m then R is invertible.
Here an example:
Definition at line 449 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction().
| unsigned int vpMatrix::qrPivot | ( | vpMatrix & | Q, |
| vpMatrix & | R, | ||
| vpMatrix & | P, | ||
| bool | full = false, |
||
| bool | squareR = false, |
||
| double | tol = 1e-6 |
||
| ) | const |
Compute the QR pivot decomposition of a (m x n) matrix of rank r. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| Q | : orthogonal matrix (will be modified). |
| R | : upper-triangular matrix (will be modified). |
| P | : the (n x n) permutation matrix. |
| full | : whether or not we want full decomposition. |
| squareR | : will return only the (r x r) part of R and the (r x n) part of P. |
| tol | : tolerance to test the rank of R. |
If full is false (default) then Q is (m x min(n,m)) and R is (min(n,m) x n). We then have this.P = Q.R.
If full is true and m > n then Q is (m x m) and R is (n x n). In this case this.P = Q (R, 0)^T
If squareR is true then R is (r x r) invertible.
Here an example:
Definition at line 1142 of file vpMatrix_qr.cpp.
References vpException::fatalError.
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
|
inlineinherited |
Definition at line 539 of file vpArray2D.h.
|
inlineinherited |
Set the size of the array and initialize all the values to zero.
| nrows | : number of rows. |
| ncols | : number of column. |
| flagNullify | : if true, then the array is re-initialized to 0 after resize. If false, the initial values from the common part of the array (common part between old and new version of the array) are kept. Default value is true. |
| recopy_ | : if true, will perform an explicit recopy of the old data. |
Definition at line 442 of file vpArray2D.h.
|
inlinestaticinherited |
Save a matrix to a file.
| filename | : Absolute file name. |
| A | : Array to be saved. |
| binary | : If true the matrix is saved in a binary file, else a text file. |
| header | : Optional line that will be saved at the beginning of the file. |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 959 of file vpArray2D.h.
|
inlinestatic |
Save a matrix to a file. This function overloads vpArray2D::save().
| filename | : Absolute file name. |
| M | : Matrix to be saved. |
| binary | : If true the matrix is save as a binary file, otherwise as a text file. |
| header | : Optional line that will be saved at the beginning of the file as a header. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.bin file where data are saved as binary data is the following:
% cat matrix.bin My header??@@@%
Definition at line 987 of file vpMatrix.h.
References vpArray2D< Type >::save().
Referenced by vpDot2::defineDots(), and vpLuminancePCA::save().
|
inlinestatic |
Save a matrix in a YAML-formatted file. This function overloads vpArray2D::saveYAML().
| filename | : Absolute file name. |
| M | : Matrix to be saved in the file. |
| header | : Optional lines that will be saved at the beginning of the file as a header. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.yaml file is the following:
% cat matrix.yaml My header rows: 2 cols: 3 data: - [-1, -2, -3] - [4, 5.5, 6]
Definition at line 1067 of file vpMatrix.h.
References vpArray2D< Type >::saveYAML().
|
inlinestaticinherited |
Save an array in a YAML-formatted file.
| filename | : absolute file name. |
| A | : array to be saved in the file. |
| header | : optional lines that will be saved at the beginning of the file. Should be YAML-formatted and will adapt to the indentation if any. |
Here is an example of outputs.
Content of matrix.yml:
Content of matrixIndent.yml:
Definition at line 1057 of file vpArray2D.h.
|
inlinestatic |
Modify default size used to determine if Blas/Lapack basic linear algebra operations are enabled.
To get more info see Tutorial: Basic linear algebra operations.
| min_size | : Minimum size of rows and columns required for a matrix or a vector to use Blas/Lapack third parties like MKL, OpenBLAS, Netlib or Atlas. When matrix or vector size is lower or equal to this parameter, Blas/Lapack is not used. In that case we prefer use naive code that runs faster for small matrices. |
Definition at line 283 of file vpMatrix.h.
|
inlineinherited |
Return the number of elements of the 2D array.
Definition at line 429 of file vpArray2D.h.
| vpColVector vpMatrix::solveByQR | ( | const vpColVector & | b | ) | const |
Solve a linear system Ax = b using QR Decomposition.
Non destructive wrt. A and B.
| b | : Vector b |
Here an example:
Definition at line 1377 of file vpMatrix_qr.cpp.
References vpArray2D< double >::colNum, and solveByQR().
| void vpMatrix::solveByQR | ( | const vpColVector & | b, |
| vpColVector & | x | ||
| ) | const |
Solve a linear system Ax = b using QR Decomposition.
Non destructive wrt. A and b.
| b | : Vector b |
| x | : Vector x |
Here an example:
Definition at line 1322 of file vpMatrix_qr.cpp.
References vpArray2D< double >::colNum, extract(), inverseTriangular(), qrPivot(), and t().
Referenced by solveByQR(), and vpQuadProg::solveSVDorQR().
| vpColVector vpMatrix::solveBySVD | ( | const vpColVector & | B | ) | const |
Solve a linear system ![]() using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| B | : Vector |
Here an example:
Definition at line 184 of file vpMatrix_svd.cpp.
References vpArray2D< double >::colNum, and solveBySVD().
| BEGIN_VISP_NAMESPACE void vpMatrix::solveBySVD | ( | const vpColVector & | b, |
| vpColVector & | x | ||
| ) | const |
Solve a linear system ![]() using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| b | : Vector |
| x | : Vector |
Here an example:
Definition at line 129 of file vpMatrix_svd.cpp.
References pseudoInverse().
Referenced by vpMeEllipse::leastSquare(), vpMeEllipse::leastSquareRobustCircle(), vpQuadProg::solveByProjection(), solveBySVD(), vpQuadProg::solveQPe(), and vpQuadProg::solveSVDorQR().
| void vpMatrix::stack | ( | const vpColVector & | c | ) |
Stack column vector c at the right of the current matrix, or copy if the matrix has no dimensions: this = [ this c ].
Here an example for a robot velocity log matrix:
Here the log matrix has size 6 rows by 100 columns.
Definition at line 312 of file vpMatrix_stack.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, vpArray2D< Type >::getRows(), vpArray2D< double >::resize(), vpArray2D< double >::rowNum, vpArray2D< double >::rowPtrs, and vpArray2D< Type >::size().
| void vpMatrix::stack | ( | const vpMatrix & | A | ) |
Stack A at the end of the current matrix, or copy if the matrix has no dimensions : this = [ this A ]^T.
Definition at line 239 of file vpMatrix_stack.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), vpArray2D< double >::resize(), and vpArray2D< double >::rowNum.
Referenced by vpFeatureVanishingPoint::interaction(), vpFeatureEllipse::interaction(), vpFeaturePoint::interaction(), vpFeaturePoint3D::interaction(), vpFeaturePointPolar::interaction(), vpFeatureSegment::interaction(), vpFeatureThetaU::interaction(), vpFeatureTranslation::interaction(), vpGenericFeature::interaction(), vpLinProg::rowReduction(), and stack().
|
static |
Stack column vector c to matrix A and return the resulting matrix [ A c ]
| A | : Left matrix. |
| c | : Right column vector. |
Definition at line 205 of file vpMatrix_stack.cpp.
References stack().
|
static |
Stack column vector c to the end of matrix A and return the resulting matrix in C.
| A | : Left matrix. |
| c | : Right column vector. |
| C | : Stacked matrix C = [ A c ] |
Definition at line 224 of file vpMatrix_stack.cpp.
References vpArray2D< Type >::data, and stack().
Stack matrix B to the end of matrix A and return the resulting matrix [ A B ]^T
| A | : Upper matrix. |
| B | : Lower matrix. |
Definition at line 102 of file vpMatrix_stack.cpp.
References stack().
Stack matrix B to the end of matrix A and return the resulting matrix in C.
| A | : Upper matrix. |
| B | : Lower matrix. |
| C | : Stacked matrix C = [ A B ]^T |
Definition at line 122 of file vpMatrix_stack.cpp.
References vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< Type >::size().
|
static |
Stack row vector r to matrix A and return the resulting matrix [ A r ]^T
| A | : Upper matrix. |
| r | : Lower row vector. |
Definition at line 166 of file vpMatrix_stack.cpp.
References stack().
|
static |
Stack row vector r to the end of matrix A and return the resulting matrix in C.
| A | : Upper matrix. |
| r | : Lower row vector. |
| C | : Stacked matrix C = [ A r ]^T |
Definition at line 185 of file vpMatrix_stack.cpp.
References vpArray2D< Type >::data, and stack().
| void vpMatrix::stack | ( | const vpRowVector & | r | ) |
Stack row vector r at the end of the current matrix, or copy if the matrix has no dimensions: this = [ this r ]^T.
Here an example for a robot velocity log :
Definition at line 271 of file vpMatrix_stack.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< double >::resize(), vpArray2D< double >::rowNum, vpArray2D< double >::size(), and vpArray2D< Type >::size().
| vpColVector vpMatrix::stackColumns | ( | ) |
Stacks columns of a matrix in a vector.
Definition at line 61 of file vpMatrix_stack.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
| BEGIN_VISP_NAMESPACE void vpMatrix::stackColumns | ( | vpColVector & | out | ) |
Stacks columns of a matrix in a vector.
| out | : a vpColVector. |
Definition at line 43 of file vpMatrix_stack.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpColVector::resize(), vpArray2D< double >::rowNum, vpArray2D< Type >::rowNum, and vpArray2D< double >::rowPtrs.
| vpRowVector vpMatrix::stackRows | ( | ) |
Stacks rows of a matrix in a vector.
Definition at line 85 of file vpMatrix_stack.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
| void vpMatrix::stackRows | ( | vpRowVector & | out | ) |
Stacks rows of a matrix in a vector
| out | : a vpRowVector. |
Definition at line 72 of file vpMatrix_stack.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpRowVector::resize(), and vpArray2D< double >::rowNum.
|
static |
Operation C = A - B on column vectors.
The result is placed in the third parameter C and not returned. A new vector won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If A and B vectors have not the same size. |
Definition at line 427 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Operation C = A - B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If A and B matrices have not the same size. |
Definition at line 461 of file vpMatrix_operations.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator-().
| double vpMatrix::sum | ( | ) | const |
Return the sum of all the 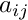 elements of the matrix.
elements of the matrix.
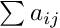
Definition at line 671 of file vpMatrix_operators.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by expm().
| double vpMatrix::sumSquare | ( | ) | const |
Return the sum square of all the ![]() elements of the matrix
elements of the matrix ![]() .
.
Definition at line 1977 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| void vpMatrix::svd | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Matrix singular value decomposition (SVD).
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default svdLapack() with a Lapack built-in version.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object `(*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 259 of file vpMatrix_svd.cpp.
References vpException::fatalError, svdEigen3(), svdLapack(), and svdOpenCV().
Referenced by vpHomogeneousMatrix::compute3d3dTransformation(), cond(), dampedInverse(), vpHomography::DLT(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), inducedL2Norm(), kernel(), vpLuminancePCA::learn(), nullSpace(), vpRotationMatrix::orthogonalize(), and svdEigen3().
| void vpMatrix::svdEigen3 | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using Eigen3 3rd party.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object (*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 643 of file vpMatrix_svd.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< double >::getCols(), vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::getRows(), vpColVector::resize(), vpArray2D< double >::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, vpArray2D< Type >::size(), and svd().
Referenced by svd().
| void vpMatrix::svdLapack | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using Lapack 3rd party.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object (*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 436 of file vpMatrix_svd.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpColVector::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and transpose().
Referenced by svd().
| void vpMatrix::svdOpenCV | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using OpenCV 3rd party.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object (*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 345 of file vpMatrix_svd.cpp.
References vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpColVector::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::resize(), and transpose().
Referenced by svd().
| BEGIN_VISP_NAMESPACE vpMatrix vpMatrix::t | ( | ) | const |
Compute and return the transpose of the matrix.
Definition at line 46 of file vpMatrix_operations.cpp.
References transpose().
Referenced by vpLinProg::colReduction(), vpHomogeneousMatrix::compute3d3dTransformation(), vpServo::computeControlLaw(), vpRBFeatureTracker::computeCovarianceMatrix(), computeCovarianceMatrix(), vpTemplateTracker::computeOptimalBrentGain(), eigenValues(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), vpKalmanFilter::filtering(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpQuadProg::fromCanonicalCost(), vpLuminanceDCT::interaction(), vpLuminanceDCT::inverse(), vpLuminancePCA::learn(), vpHomogeneousMatrix::mean(), vpRotationMatrix::mean(), operator=(), vpRotationMatrix::orthogonalize(), vpKalmanFilter::prediction(), vpLinProg::simplex(), solveByQR(), and vpMatrix().
| vpMatrix vpMatrix::transpose | ( | ) | const |
Compute and return the transpose of the matrix.
Definition at line 53 of file vpMatrix_operations.cpp.
Referenced by vpLinProg::colReduction(), dampedInverse(), vpQuadProg::fromCanonicalCost(), vpLuminancePCA::learn(), vpLinProg::rowReduction(), vpLinProg::solveLP(), vpQuadProg::solveQPi(), svdLapack(), svdOpenCV(), t(), and vpUnscentedKalman::update().
| void vpMatrix::transpose | ( | vpMatrix & | At | ) | const |
Compute At the transpose of the matrix.
| At | (output) : Resulting transpose matrix. |
Definition at line 65 of file vpMatrix_operations.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
|
inlinestaticinherited |
Creates a view of the Matrix A. A view shares the same underlying memory as the original array. It can be written into, modifying the original data. However, the array cannot be resized.
When you use this method, it is your responsibility to ensure that the lifespan of the view does not exceed the lifespan of the original array.
| A | the array to view |
Definition at line 323 of file vpArray2D.h.
|
static |
Create a matrix view of a raw data array. The view can modify the contents of the raw data array, but may not resize it and does not own it: the memory is not released by the matrix and it should be freed by the user after the matrix view is released.
| data | the raw data |
| rows | Number of rows |
| cols | Number of columns |
Definition at line 306 of file vpMatrix.cpp.
References vpArray2D< double >::data, and vpArray2D< Type >::view().
|
inlinestaticinherited |
Create an array view of a raw data pointer. After this function has been called, the array data can be modified through the view v. This data is not owned by the resulting array and should be freed after the array is destroyed (not before).
| v | The resulting view array |
| data | Pointer to the raw data |
| numRows | Number of rows |
| numCols | Number of columns |
Definition at line 362 of file vpArray2D.h.
|
related |
Insert array B in array A at the given position.
| A | : Main array. |
| B | : Array to insert. |
| C | : Result array. |
| r | : Index of the row where to insert array B. |
| c | : Index of the column where to insert array B. |
Definition at line 1181 of file vpArray2D.h.
|
related |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| C | : Result matrix. |
| r | : Index of the row where to insert matrix B. |
| c | : Index of the column where to insert matrix B. |
Definition at line 743 of file vpMatrix.cpp.
|
related |
Definition at line 1441 of file vpArray2D.h.
Allow to multiply a scalar by a matrix.
Definition at line 800 of file vpMatrix_operators.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
|
related |
Definition at line 1403 of file vpArray2D.h.
|
related |
Definition at line 1422 of file vpArray2D.h.
|
related |
This function performs generalized matrix multiplication: D = alpha*op(A)*op(B) + beta*op(C), where op(X) is X or X^T. Operation on A, B and C matrices is described by enumeration vpGEMMmethod().
For example, to compute D = alpha*A^T*B^T+beta*C we need to call :
If C is not used, vpGEMM must be called using an empty array null. Thus to compute D = alpha*A^T*B, we have to call:
| vpException::incorrectMatrixSizeError | if the sizes of the matrices do not allow the operations. |
| A | : An array that could be a vpMatrix. |
| B | : An array that could be a vpMatrix. |
| alpha | : A scalar. |
| C | : An array that could be a vpMatrix. |
| beta | : A scalar. |
| D | : The resulting array that could be a vpMatrix. |
| ops | : A scalar describing operation applied on the matrices. Possible values are the one defined in vpGEMMmethod(): VP_GEMM_A_T, VP_GEMM_B_T, VP_GEMM_C_T. |
|
related |
Enumeration of the operations applied on matrices in vpGEMM() function.
Operations are :
|
protectedinherited |
Number of columns in the array.
Definition at line 1188 of file vpArray2D.h.
|
inherited |
Address of the first element of the data array.
Definition at line 148 of file vpArray2D.h.
|
protectedinherited |
Current array size (rowNum * colNum)
Definition at line 1192 of file vpArray2D.h.
|
protectedinherited |
Whether this array owns the memory it points to.
Definition at line 1194 of file vpArray2D.h.
|
protectedinherited |
Whether this array owns the row pointers.
Definition at line 1196 of file vpArray2D.h.
|
protectedinherited |
Number of rows in the array.
Definition at line 1186 of file vpArray2D.h.
|
protectedinherited |
Address of the first element of each rows.
Definition at line 1190 of file vpArray2D.h.