Introduction

The Unscented Kalman Filter (UKF) is a version of the Kalman filter that handles non-linearities.

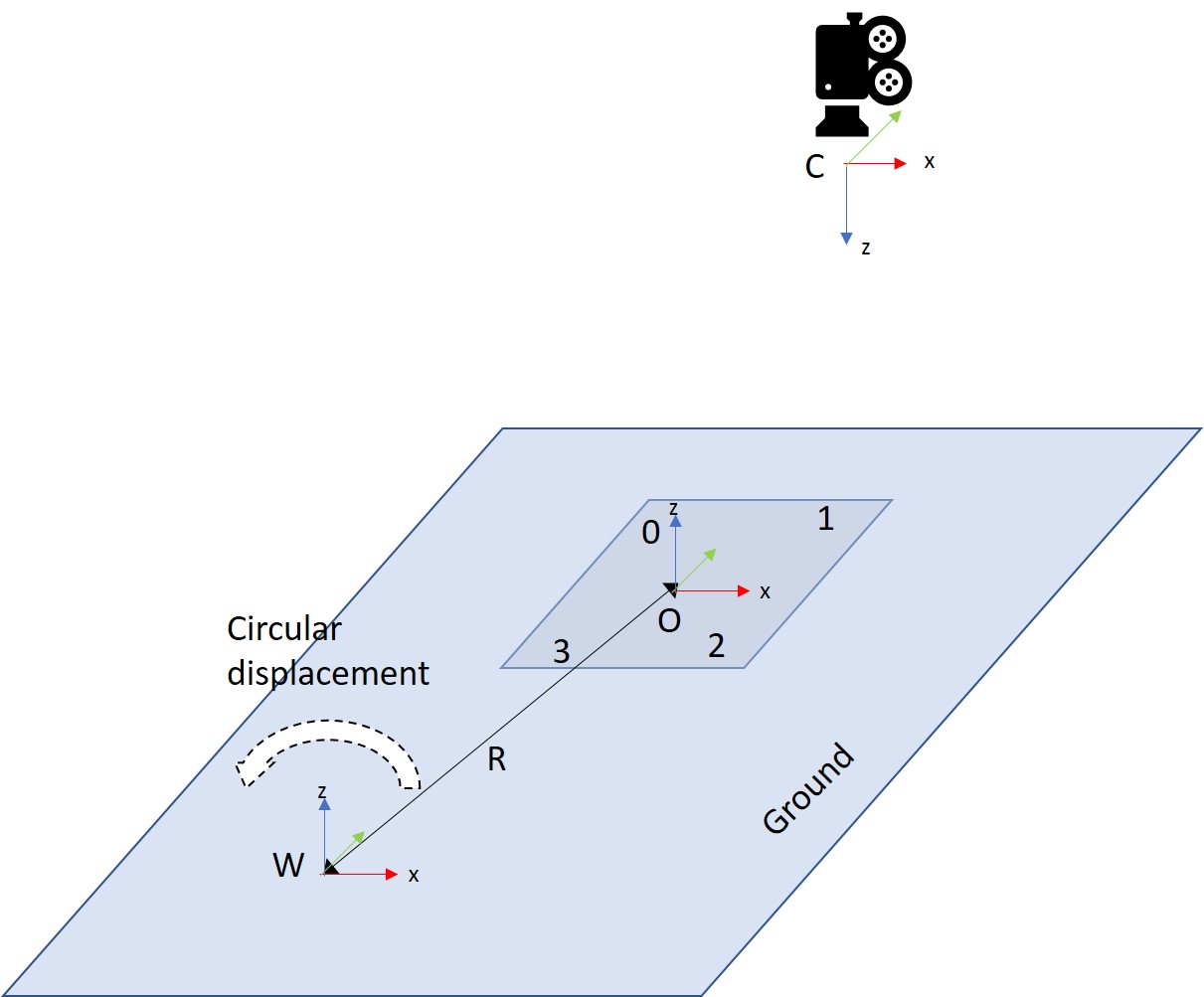
In this tutorial, we will use a UKF to filter the 3D position of a simulated object, which revolves in a plane parallel to the ground around a static point, which is the origin of the world frame ${F}_W$ . The coordinate frame attached to the object is denoted ${F}_O$ . The object is observed by a static camera whose coordinate frame is denoted ${F}_C$ . The object is supposed plane and having four markers sticked on its surface.

The equations that describe the motion of the object in the world frame are the following:

$\begin{array}{lcl} {}^W \textbf{X}_x &=& R cos(\omega t + \phi) \\ {}^W \textbf{X}_y &=& R sin(\omega t + \phi) \\ {}^W \textbf{X}_z &=& constant \end{array}$

where $\omega$ and $\phi$ are respectively the pulsation and the phase of the motion, while is the radius of the revolution around the origin of the world frame.

The maths beyond the Unscented Kalman Filter

The maths beyond the Unscented Kalman Filter are explained in the documentation of the vpUnscentedKalman class. We will recall briefly the important steps of the UKF.

Be $\textbf{x} \in {R}^n$ the internal state of the UKF and $\textbf{P} \in {R}^{n\text{ x }n}$ the associated covariance matrix.

The first step of the UKF is the prediction step. During this step, some particular points called sigma points, denoted $\chi$ , are drawn along with associated weights $\textbf{w}^m$ for the computation of the mean and $\textbf{w}^c$ for the computation of the covariance:

$\begin{array}{lcl} \chi &=& sigma-function(\textbf{x}, \textbf{P}) \\ \textbf{w}^m, \textbf{w}^c &=& weight-function(n, parameters) \end{array}$

There are different ways of drawing the sigma points and associated weights in the litterature, such as the one proposed by Julier or the one proposed by E. A. Wan and R. van der Merwe in [51].

Be $\textbf{u}$ the vector containing the known commands sent to the system, if any. Then, we pass each sigma point through the process function $f(\chi, \Delta t)$ , the command function $b( \textbf{u}, \Delta t )$ and the command function depending on the state $bx( \textbf{u}, \chi, \Delta t )$ to project them forward in time, forming the new prior:

${Y} = f( \chi , \Delta t ) + b( \textbf{u}, \Delta t ) + bx( \textbf{u}, \chi, \Delta t )$

Finally, we apply the Unscented Transform to compute the mean $\boldsymbol{\mu}$ and covariance $\overline{\textbf{P}}$ of the prior:

$\begin{array}{lcl} \boldsymbol{\mu}, \overline{\textbf{P}} &=& UT({Y}, \textbf{w}^m, \textbf{w}^c, \textbf{Q}) \\ \boldsymbol{\mu} &=& \sum_{i=0}^{2n} w_i^m {Y}_i \\ \overline{\textbf{P}} &=& \sum_{i=0}^{2n} ( w_i^c ({Y}_i - \boldsymbol{\mu}) ({Y}_i - \boldsymbol{\mu})^T ) + \textbf{Q} \end{array}$

where $\textbf{Q}$ is the covariance of the error introduced by the process function.

The second step of the UKF is to update the internal state based on new measurements. It is performed in the measurement space, so we must convert the sigma points of the prior into measurements using the measurement function $h: {R}^n \rightarrow {R}^m$ :

Then, we use once again the Unscented Transform to compute the mean $\boldsymbol{\mu}_z \in {R}^m$ and the covariance $\textbf{P}_z \in {R}^{m\text{ x }m}$ of these points:

$\begin{array}{lcl} \boldsymbol{\mu}_z, \textbf{P}_z &=& UT({Z}, \textbf{w}^m, \textbf{w}^c, \textbf{R}) \\ \boldsymbol{\mu}_z &=& \sum_{i=0}^{2n} w_i^m {Z}_i \\ \textbf{P}_z &=& \sum_{i=0}^{2n} ( w_i^c ({Z}_i - \boldsymbol{\mu}_z) ({Z}_i - \boldsymbol{\mu}_z)^T ) + \textbf{R} \end{array}$

where $\textbf{R}$ is the measurement covariance matrix.

Then, we compute the residual $\textbf{y}$ of the measurement $\textbf{z}$ :

$\textbf{y} = \textbf{z} - \boldsymbol{\mu}_z$

To compute the Kalman's gain, we first need to compute the cross covariance of the state and the measurements:

$\textbf{P}_{xy} = \sum_{i=0}^{2n} w_i^c ({Y}_i - \boldsymbol{\mu})({Z}_i - \boldsymbol{\mu}_z)^T$

The Kalman's gain is then defined as:

$\textbf{K} = \textbf{P}_{xz} \textbf{P}_z^{-1}$

Finally, we can compute the new state estimate $\textbf{x}$ and the new covariance $\textbf{P}$ :

$\begin{array}{lcl} \textbf{x} &=& \boldsymbol{\mu} + \textbf{K} \textbf{y} \\ \textbf{P} &=& \overline{\textbf{P}} - \textbf{K} \textbf{P}_z \textbf{K}^T \end{array}$

Explanations about the tutorial

How to run the tutorial

To run the tutorial, please run the following commands:

$ cd $VISP_WS/visp-build/tutorial/kalman

$ ./tutorial-ukf

visp

Definition: vpIoTools.h:61

The program does not take any argument. You should see something similar to the following image:

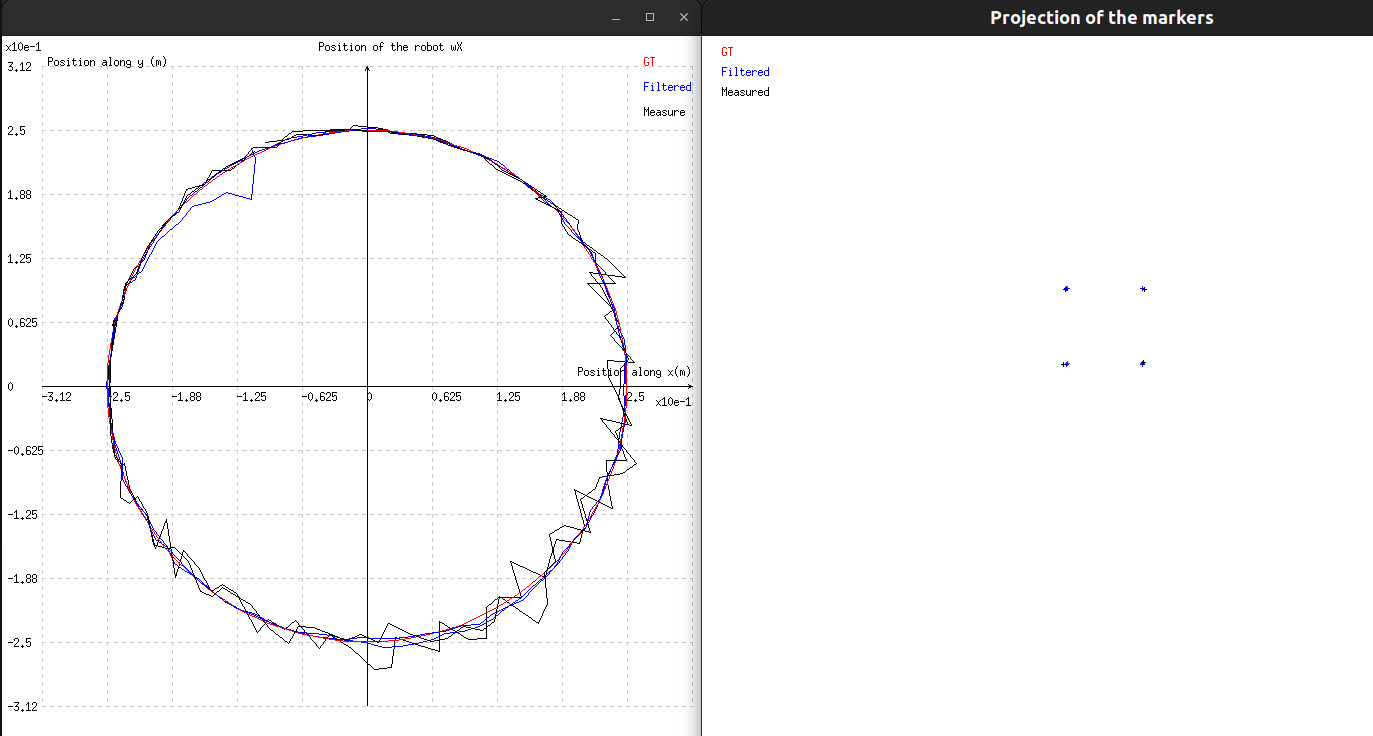
Screenshot of the tutorial Graphical User Interface

Press Return to leave the program.

Detailed explanations about the UKF tutorial

For this tutorial, we use the main program tutorial-ukf.cpp . The internal state of the UKF is the 3D position of the object expressed in the world frame, along with the pulsation $\omega$ of the motion:

$\begin{array}{lcl} \textbf{x}[0] &=& {}^WX_x \\ \textbf{x}[1] &=& {}^WX_y \\ \textbf{x}[2] &=& {}^WX_z \\ \textbf{x}[3] &=& \omega \Delta t \end{array}$

The measurement $\textbf{z}$ corresponds to the perspective projection of the different markers in the image. Be and the horizontal and vertical pixel coordinates of the $i^{th}$ marker. The measurement vector can be written as:

$\begin{array}{lcl} \textbf{z}[2i] &=& u_i \\ \textbf{z}[2i+1] &=& v_i \end{array}$

Be $\textbf{K}_{intr}$ the camera instrinsic parameters matrix defined by:

$\textbf{K}_{intr} = \begin{pmatrix} p_x & 0 & u_0 \\ 0 & p_y & v_0 \\ 0 & 0 & 1 \end{pmatrix}$

where are the coordinates of the principal point and (resp. ) is the ratio between the focal lens of the camera and the width (resp. height) of a pixel.

Be $\boldsymbol{\pi}$ the projection matrix that is, in the case of a perspective projection model, given by:

$\boldsymbol{\pi} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}$

The perspective projection $\textbf{p} = (u, v, 1)^T$ of a point ${}^W\textbf{X} = ({}^WX_x, {}^WX_y, {}^WX_z, 1)^T$ is given by:

$\textbf{p} = \textbf{K}_{intr} \boldsymbol{\pi} {}^C\textbf{M}_W {}^W\textbf{X}$

where ${}^C\textbf{M}_W$ is the homogeneous matrix that expresses the pose of the world coordinate frame ${F}_W$ with regard to the camera frame ${F}_C$ .

Details on the includes

To have a Graphical User Interface (GUI), we include the following files.

#ifdef VISP_HAVE_DISPLAY
#include <visp3/gui/vpPlot.h>
#include <visp3/gui/vpDisplayFactory.h>
#endif

To be able to use the UKF, we use the following includes:

#include <visp3/core/vpUKSigmaDrawerMerwe.h>

#include <visp3/core/vpUnscentedKalman.h>

Details on the class simulating a moving object

To make simpler the main loop of the program, we decided to implement a class that will update the 3D position of the object, expressed in the world frame, in a dedicated class.

 
class vpObjectSimulator
{
public:
  vpObjectSimulator(const double &R, const double &w, const double &phi, const double &wZ)
    : m_R(R)
    , m_w(w)
    , m_phi(phi)
    , m_wZ(wZ)
  { }
 
  vpColVector move(const double &t) const
  {
    vpColVector wX(4, 1.);
    wX[0] = m_R * std::cos(m_w * t + m_phi);
    wX[1] = m_R * std::sin(m_w * t + m_phi);
    wX[2] = m_wZ;
    return wX;
  }
 
private:
  double m_R; // Radius of the revolution around the world frame origin.
  double m_w; // Pulsation of the motion.
  double m_phi; // Phase of the motion.
  const double m_wZ; // The z-coordinate of the object in the world frame.
};

Details on the process function

As mentionned in The maths beyond the Unscented Kalman Filter, the UKF relies on a process function which project in time the internal state of the UKF.

We want to express the internal state projected in the future $\textbf{x}_{t + \Delta t}$ as a function of its previous state $\textbf{x}_{t}$ .

As stated in the Introduction, the equations of motion of the object are the following:

$\begin{array}{lcl} {}^W X_x(t) &=& R cos(\omega t + \phi) \\ {}^W X_y(t) &=& R sin(\omega t + \phi) \\ {}^W X_z(t) &=& constant \end{array}$

Thus, we have:

$\begin{array}{lclcl} {}^WX_x( t + \Delta t) &=& R cos(\omega (t + \Delta t) + \phi) &=& R cos((\omega t + \phi) + \omega \Delta t )\\ {}^WX_y( t + \Delta t) &=& R sin(\omega (t + \Delta t) + \phi) &=& R sin((\omega t + \phi) + \omega \Delta t )\\ {}^WX_z( t + \Delta t) &=& constant \end{array}$

Which can be rewritten:

$\begin{array}{lclcl} {}^WX_x( t + \Delta t) &=& R cos((\omega t + \phi) + \omega \Delta t ) &=& R cos(\omega t + \phi) cos (\omega \Delta t ) - R sin(\omega t + \phi) sin(\omega \Delta t) \\ {}^WX_y( t + \Delta t) &=& R sin((\omega t + \phi) + \omega \Delta t ) &=& R cos(\omega t + \phi) sin (\omega \Delta t ) + R sin(\omega t + \phi) cos(\omega \Delta t)\\ {}^WX_z( t + \Delta t) &=& constant \end{array}$

And can be finally written as:

$\begin{array}{lclcl} {}^WX_x( t + \Delta t) &=& R cos(\omega t + \phi) cos (\omega \Delta t ) - R sin(\omega t + \phi) sin(\omega \Delta t) &=& {}^W X_x( t) cos(\omega \Delta t) - {}^W X_y(t) sin(\omega \Delta t) \\ {}^WX_y( t + \Delta t) &=& R cos(\omega t + \phi) sin (\omega \Delta t ) + R sin(\omega t + \phi) cos(\omega \Delta t) &=& {}^W X_x( t) sin(\omega \Delta t) + {}^W X_y(t) cos(\omega \Delta t) \\ {}^WX_z( t + \Delta t) &=& constant \end{array}$

This motivates us to choose the following non-linear process function:

$\begin{array}{lclcl} \textbf{x}[0]_{t + \Delta t} &=& {}^WX_x (t + \Delta t) &=& \textbf{x}[0]_{t} cos(\textbf{x}[3]_{t}) - \textbf{x}[1]_{t} sin(\textbf{x}[3]_{t}) \\ \textbf{x}[1]_{t + \Delta t} &=& {}^WX_y (t + \Delta t) &=& \textbf{x}[0]_{t} sin(\textbf{x}[3]_{t}) + \textbf{x}[1]_{t} cos(\textbf{x}[3]_{t}) \\ \textbf{x}[2]_{t + \Delta t} &=& {}^WX_z (t + \Delta t) &=& \textbf{x}[2]_{t} \\ \textbf{x}[3]_{t + \Delta t} &=& \omega \Delta t &=& \textbf{x}[3]_{t} \end{array}$

As the process function is pretty simple, a simple function called here fx() is enough:

 
vpColVector fx(const vpColVector &x, const double & /*dt*/)
{
  vpColVector x_kPlus1(4);
  x_kPlus1[0] = x[0] * std::cos(x[3]) - x[1] * std::sin(x[3]); // wX
  x_kPlus1[1] = x[0] * std::sin(x[3]) + x[1] * std::cos(x[3]); // wY
  x_kPlus1[2] = x[2]; // wZ
  x_kPlus1[3] = x[3]; // omega * dt
  return x_kPlus1;
}

Details on the class simulating marker measurement

The measurements of the projection of the markers in the image are handled by the following class:

 
class vpMarkersMeasurements
{
public:
  vpMarkersMeasurements(const vpCameraParameters &cam, const vpHomogeneousMatrix &cMw, const vpRotationMatrix &wRo,
                        const std::vector<vpColVector> &markers, const double &noise_stdev, const long &seed)
    : m_cam(cam)
    , m_cMw(cMw)
    , m_wRo(wRo)
    , m_markers(markers)
    , m_rng(noise_stdev, 0., seed)
  { }
 
 
  vpColVector state_to_measurement(const vpColVector &x)
  {
    unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
    vpColVector meas(2*nbMarkers);
    vpHomogeneousMatrix wMo;
    vpTranslationVector wTo(x[0], x[1], x[2]);
    wMo.buildFrom(wTo, m_wRo);
    for (unsigned int i = 0; i < nbMarkers; ++i) {
      vpColVector cX = m_cMw * wMo * m_markers[i];
      double u = 0., v = 0.;
      vpMeterPixelConversion::convertPoint(m_cam, cX[0] / cX[2], cX[1] / cX[2], u, v);
      meas[2*i] = u;
      meas[2*i + 1] = v;
    }
    return meas;
  }
 
 
  vpColVector measureGT(const vpColVector &wX)
  {
    unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
    vpColVector meas(2*nbMarkers);
    vpHomogeneousMatrix wMo;
    vpTranslationVector wTo(wX[0], wX[1], wX[2]);
    wMo.buildFrom(wTo, m_wRo);
    for (unsigned int i = 0; i < nbMarkers; ++i) {
      vpColVector cX = m_cMw * wMo * m_markers[i];
      double u = 0., v = 0.;
      vpMeterPixelConversion::convertPoint(m_cam, cX[0] / cX[2], cX[1] / cX[2], u, v);
      meas[2*i] = u;
      meas[2*i + 1] = v;
    }
    return meas;
  }
 
 
  vpColVector measureWithNoise(const vpColVector &wX)
  {
    vpColVector measurementsGT = measureGT(wX);
    vpColVector measurementsNoisy = measurementsGT;
    unsigned int sizeMeasurement = measurementsGT.size();
    for (unsigned int i = 0; i < sizeMeasurement; ++i) {
      measurementsNoisy[i] += m_rng();
    }
    return measurementsNoisy;
  }
 
private:
  vpCameraParameters m_cam; // The camera parameters
  vpHomogeneousMatrix m_cMw; // The pose of the world frame with regard to the camera frame.
  vpRotationMatrix m_wRo; // The rotation matrix that expresses the rotation between the world frame and object frame.
  std::vector<vpColVector> m_markers; // The position of the markers in the object frame.
  vpGaussRand m_rng; // Noise simulator for the measurements
};

It takes as input the camera parameters cam, the homogeneous matrix expressing the pose of the world frame ${F}_W$ with regard to the camera frame ${F}_C$ cMw, the rotation matrix that expresses the rotation between the object frame and world frame wRo and the homogeneous coordinates of the markers expressed in the object frame markers to be able to convert the 3D position of the object in the world frame ${}^W \textbf{X}$ into 3D positions of the markers in the camera frame ${}^C \textbf{X}^i$ , where $ i $ 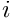denotes the i $^{th}$ marker sticked on the object. The standard deviation of the noise noise_stdev and the seed value seed are here to initialized the Gaussian noise generator used to simulate noisy measurements.

The method state_to_measurement is used to convert the internal state of the UKF into the measurement space (i.e. the projection in the image of the markers sticked on the object if the object is at this 3D position):

 
  vpColVector state_to_measurement(const vpColVector &x)
  {
    unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
    vpColVector meas(2*nbMarkers);
    vpHomogeneousMatrix wMo;
    vpTranslationVector wTo(x[0], x[1], x[2]);
    wMo.buildFrom(wTo, m_wRo);
    for (unsigned int i = 0; i < nbMarkers; ++i) {
      vpColVector cX = m_cMw * wMo * m_markers[i];
      double u = 0., v = 0.;
      vpMeterPixelConversion::convertPoint(m_cam, cX[0] / cX[2], cX[1] / cX[2], u, v);
      meas[2*i] = u;
      meas[2*i + 1] = v;
    }
    return meas;
  }

The method measureGT is used to convert the ground truth 3D position of the object into ground truth projections of the markers in the image:

 
  vpColVector measureGT(const vpColVector &wX)
  {
    unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
    vpColVector meas(2*nbMarkers);
    vpHomogeneousMatrix wMo;
    vpTranslationVector wTo(wX[0], wX[1], wX[2]);
    wMo.buildFrom(wTo, m_wRo);
    for (unsigned int i = 0; i < nbMarkers; ++i) {
      vpColVector cX = m_cMw * wMo * m_markers[i];
      double u = 0., v = 0.;
      vpMeterPixelConversion::convertPoint(m_cam, cX[0] / cX[2], cX[1] / cX[2], u, v);
      meas[2*i] = u;
      meas[2*i + 1] = v;
    }
    return meas;
  }

The method measureWithNoise adds noise to the ground truth measurements in order to simulate a noisy measurement process:

 
  vpColVector measureWithNoise(const vpColVector &wX)
  {
    vpColVector measurementsGT = measureGT(wX);
    vpColVector measurementsNoisy = measurementsGT;
    unsigned int sizeMeasurement = measurementsGT.size();
    for (unsigned int i = 0; i < sizeMeasurement; ++i) {
      measurementsNoisy[i] += m_rng();
    }
    return measurementsNoisy;
  }

Details on the computation of the pose from noisy measurements

The method computePose compute the 3D pose of an object from the 3D coordinates along with their projection in the image. Here, we use it to convert the noisy measurements in a noisy 3D pose, in order to compare the 3D position estimated by the UKF with regard to the 3D position we would have if we computed the pose directly from the noisy measurements.

 
vpHomogeneousMatrix computePose(std::vector<vpPoint> &point, const std::vector<vpImagePoint> &ip, const vpCameraParameters &cam)
{
  vpPose pose;
  double x = 0, y = 0;
  for (unsigned int i = 0; i < point.size(); i++) {
    vpPixelMeterConversion::convertPoint(cam, ip[i], x, y);
    point[i].set_x(x);
    point[i].set_y(y);
    pose.addPoint(point[i]);
  }
 
  vpHomogeneousMatrix cMo;
  pose.computePose(vpPose::DEMENTHON_LAGRANGE_VIRTUAL_VS, cMo);
  return cMo;
}

Details on the constants of the main loop

In the main loop of the program, we first declare some constants that will be used later on:

  const double dt = 0.001; // Period of 0.1s
  const double sigmaMeasurements = 2.; // Standard deviation of the measurements: 2 pixels
  const double radius = 0.25; // Radius of revolution of 0.25m
  const double w = 2 * M_PI * 10; // Pulsation of the motion of revolution
  const double phi = 2; // Phase of the motion of revolution
 
  // Vector of the markers sticked on the object
  const std::vector<vpColVector> markers = { vpColVector({-0.05, 0.05, 0., 1.}),
                                             vpColVector({0.05, 0.05, 0., 1.}),
                                             vpColVector({0.05, -0.05, 0., 1.}),
                                             vpColVector({-0.05, -0.05, 0., 1.}) };
  const unsigned int nbMarkers = static_cast<unsigned int>(markers.size());
  std::vector<vpPoint> markersAsVpPoint;
  for (unsigned int i = 0; i < nbMarkers; ++i) {
    vpColVector marker = markers[i];
    markersAsVpPoint.push_back(vpPoint(marker[0], marker[1], marker[2]));
  }
 
  const long seed = 42; // Seed for the random generator
  vpHomogeneousMatrix cMw; // Pose of the world frame with regard to the camera frame
  cMw[0][0] = 1.; cMw[0][1] = 0.; cMw[0][2] = 0.; cMw[0][3] = 0.2;
  cMw[1][0] = 0.; cMw[1][1] = -1.; cMw[1][2] = 0.; cMw[1][3] = 0.3;
  cMw[2][0] = 0.; cMw[2][1] = 0.; cMw[2][2] = -1.; cMw[2][3] = 1.;
 
  vpHomogeneousMatrix wMo; // Pose of the object frame with regard to the world frame
  wMo[0][0] = 1.; wMo[0][1] = 0.; wMo[0][2] = 0.; wMo[0][3] = radius;
  wMo[1][0] = 0.; wMo[1][1] = 1.; wMo[1][2] = 0.; wMo[1][3] = 0;
  wMo[2][0] = 0.; wMo[2][1] = 0.; wMo[2][2] = 1.; wMo[2][3] = 0.2;
  vpRotationMatrix wRo; // Rotation between the object frame and world frame
  wMo.extract(wRo);
  const double wZ = wMo[2][3];

Here is their meanings:

dt is the sampling period (the time spent between two acquisitions),
sigmaMeasurements is the standard deviation of the Gaussian noise added to the measurements,
radius is the radius of the revolution of the object around the world frame origin,
w is the pulsation of the motion of revolution,
phi is the phase of the motion of revolution,
markers is a vector containing the homogeneous coordinates expressed in the object frame of the markers,
markersAsVpPoint is a vector containing the 3D coordinates of the markers expressed in the object (to compute the noisy pose as explained previously),
seed is the seed for the Gaussian noise generator that adds noise to the projections of the markers in the image,
cMw is the homogeneous matrix expressing the pose of the world frame with regard to the camera frame,
wMo is the homogeneous matrix expressing the pose of the object frame with regard to the world frame,
wRo is the rotation matrix contained in wMo
wZ is the z-axis coordinate of the origin of the object frame expressed in the world frame.

To convert the 3D position of the object into the projection of its markers in the image, we need camera parameters. We generate camera parameters for a simulated camera as follow:

  // Create a camera parameter container
  // Camera initialization with a perspective projection without distortion model
  double px = 600; double py = 600; double u0 = 320; double v0 = 240;
  vpCameraParameters cam;
  cam.initPersProjWithoutDistortion(px, py, u0, v0);

Details on the initialization of the UKF

To initialize the UKF, we need an object that will be able to compute the sigma points and their associated weights. To do so, we must create an instance of a class inheriting from the class vpUKSigmaDrawerAbstract. In our case, we decided to use the method proposed by E. A. Wan and R. van der Merwe in [51] and implemented in the vpUKSigmaDrawerMerwe class:

std::shared_ptr<vpUKSigmaDrawerAbstract> drawer = std::make_shared<vpUKSigmaDrawerMerwe>(4, 0.001, 2., -1);

The first parameter is the dimension of the state of the UKF. The second parameter is 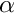$\alpha$ : the greater it is the further of the mean the sigma points are; it is a real and its value must be between 0 and 1. The third parameter is $\beta$ : it is a real whose value is set to two for Gaussian problems. Finally, the last parameter is $\kappa$ : it is a real whose value must be set to for most problems.

The UKF needs the covariance matrix of the measurements $\textbf{R}$ that represents the uncertainty of the measurements:

  vpMatrix R1landmark(2, 2, 0.); // The covariance of the noise introduced by the measurement with 1 landmark
  R1landmark[0][0] = sigmaMeasurements*sigmaMeasurements;
  R1landmark[1][1] = sigmaMeasurements*sigmaMeasurements;
  vpMatrix R(2*nbMarkers, 2 * nbMarkers);
  for (unsigned int i = 0; i < nbMarkers; ++i) {
    R.insert(R1landmark, 2*i, 2*i);
  }

The UKF needs the covariance matrix of the process $\textbf{Q}$ that represents the uncertainty induced during the prediction step:

  const double processVariance = 0.000025; // Variance of the process of (0.005cm)^2
  vpMatrix Q; // The covariance of the process
  Q.eye(4);
  Q = Q * processVariance;

The UKF needs an estimate of the intial state $\textbf{x}_0$ and of its covariance $\textbf{P}_0$ :

  vpMatrix P0(4, 4); //  The initial guess of the process covariance
  P0.eye(4);
  P0[0][0] = 1.;
  P0[1][1] = 1.;
  P0[2][2] = 1.;
  P0[2][2] = 5.;
 
  vpColVector X0(4); // The initial guess for the state
  X0[0] = radius; // wX = radius m
  X0[1] = 0.; // wY = 0m
  X0[2] = 0.95 * wZ; // Wrong estimation of the position along the z-axis: error of 5%
  X0[3] = 0.75 * w * dt; // Wrong estimation of the pulsation: error of 25%

Next, we initialize the process function and the measurement function:

  vpUnscentedKalman::vpProcessFunction f = fx;
  vpMarkersMeasurements markerMeas(cam, cMw, wRo, markers, sigmaMeasurements, seed);
  using std::placeholders::_1;
  vpUnscentedKalman::vpMeasurementFunction h = std::bind(&vpMarkersMeasurements::state_to_measurement, &markerMeas, _1);

Finally, we create the UKF and initialize its state:

  // Initialize the UKF
  vpUnscentedKalman ukf(Q, R, drawer, f, h);
  ukf.init(X0, P0);

If the internal state cannot use the standard addition and subtraction, it would be necessary to write other methods:

a method permitting to add two state vectors (see vpUnscentedKalman::setStateAddFunction),
a method permitting to subtract two state vectors (see vpUnscentedKalman::setStateResidualFunction),
and a method permitting to compute the mean of several state vectors (see vpUnscentedKalman::setStateMeanFunction).

If some commands are known to have an effect on the internal state, it would be necessary to write other methods:

a method for the effects of the commands on the state, without knowing the state (see vpUnscentedKalman::setCommandOnlyFunction),
and/or a method for the effects of the commands on the state, knowing the state (see vpUnscentedKalman::setCommandStateFunction).

If the measurement space cannot use the standard addition and subtraction, it would be necessary to write other methods:

a method permitting to subtract two measurement vectors (see vpUnscentedKalman::setMeasurementResidualFunction),
and a method permitting to compute the mean of several measurement vectors (see vpUnscentedKalman::setMeasurementMeanFunction).

Details on the initialization of the Graphical User Interface

If ViSP has been compiled with any of the third-party graphical libraries, we first begin by initializing the plot that will display the object x and y coordinates expressed in the world frame:

#ifdef VISP_HAVE_DISPLAY
  // Initialize the plot
  vpPlot plot(1);
  plot.initGraph(0, 3);
  plot.setTitle(0, "Position of the robot wX");
  plot.setUnitX(0, "Position along x(m)");
  plot.setUnitY(0, "Position along y (m)");
  plot.setLegend(0, 0, "GT");
  plot.setLegend(0, 1, "Filtered");
  plot.setLegend(0, 2, "Measure");
  plot.initRange(0, -1.25 * radius, 1.25 * radius, -1.25 * radius, 1.25 * radius);
  plot.setColor(0, 0, vpColor::red);
  plot.setColor(0, 1, vpColor::blue);
  plot.setColor(0, 2, vpColor::black);
#endif

Then, we initialize the simple renderer that displays what the camera sees:

  // Initialize the display
  // Depending on the detected third party libraries, we instantiate here the
  // first video device which is available
#ifdef VISP_HAVE_DISPLAY
  vpImage<vpRGBa> Idisp(700, 700, vpRGBa(255));
  std::shared_ptr<vpDisplay> d = vpDisplayFactory::createDisplay(Idisp, 800, -1, "Projection of the markers");
#endif

Details on the initialization of the loop

For the initialization of the loop, we initialize an instance of the vpObjectSimulator class that simulates the moving object. Then, we initialize the current ground-truth 3D position of the object expressed in the world frame, which is the frame in which the internal state of the UKF is expressed, as a null homogeneous coordinates vector.

  // Initialize the simulation
  vpObjectSimulator object(radius, w, phi, wZ);
  vpColVector object_pos(4, 0.);
  object_pos[3] = 1.;

Details on the loop

The main loop of the program is the following:

  for (unsigned int i = 0; i < 200; ++i) {
    // Update object pose
    object_pos = object.move(dt * static_cast<double>(i));
 
    // Perform the measurement
    vpColVector z = markerMeas.measureWithNoise(object_pos);
 
    // Use the UKF to filter the measurement
    ukf.filter(z, dt);
 
#ifdef VISP_HAVE_DISPLAY
    // Prepare the pose computation:
    // the image points corresponding to the noisy markers are needed
    std::vector<vpImagePoint> ip;
    for (unsigned int id = 0; id < nbMarkers; ++id) {
      vpImagePoint markerProjNoisy(z[2*id + 1], z[2*id]);
      ip.push_back(markerProjNoisy);
    }
 
    // Compute the pose using the noisy markers
    vpHomogeneousMatrix cMo_noisy = computePose(markersAsVpPoint, ip, cam);
    vpHomogeneousMatrix wMo_noisy = cMw.inverse() * cMo_noisy;
    double wXnoisy = wMo_noisy[0][3];
    double wYnoisy = wMo_noisy[1][3];
 
    // Plot the ground truth
    plot.plot(0, 0, object_pos[0], object_pos[1]);
 
    // Plot the filtered state
    vpColVector Xest = ukf.getXest();
    plot.plot(0, 1, Xest[0], Xest[1]);
 
    // Plot the noisy pose
    plot.plot(0, 2, wXnoisy, wYnoisy);
 
    // Display the projection of the markers
    vpDisplay::display(Idisp);
    vpColVector zGT = markerMeas.measureGT(object_pos);
    vpColVector zFilt = markerMeas.state_to_measurement(Xest);
    for (unsigned int id = 0; id < nbMarkers; ++id) {
      vpImagePoint markerProjGT(zGT[2*id + 1], zGT[2*id]);
      vpDisplay::displayCross(Idisp, markerProjGT, 5, vpColor::red);
 
      vpImagePoint markerProjFilt(zFilt[2*id + 1], zFilt[2*id]);
      vpDisplay::displayCross(Idisp, markerProjFilt, 5, vpColor::blue);
 
      vpImagePoint markerProjNoisy(z[2*id + 1], z[2*id]);
      vpDisplay::displayCross(Idisp, markerProjNoisy, 5, vpColor::black);
    }
 
    vpImagePoint ipText(20, 20);
    vpDisplay::displayText(Idisp, ipText, std::string("GT"), vpColor::red);
    ipText.set_i(ipText.get_i() + 20);
    vpDisplay::displayText(Idisp, ipText, std::string("Filtered"), vpColor::blue);
    ipText.set_i(ipText.get_i() + 20);
    vpDisplay::displayText(Idisp, ipText, std::string("Measured"), vpColor::black);
    vpDisplay::flush(Idisp);
    vpTime::wait(40);
#endif
  }

First, we update the ground-truth 3D position of the object based on the simulated time using the following line:

// Update object pose

object_pos = object.move(dt * static_cast<double>(i));

Then, we update the measurement by projecting the 3D position of the markers attached to the object in the image and add some noise to the projections using the following line:

// Perform the measurement

vpColVector z = markerMeas.measureWithNoise(object_pos);

Then, we use the Unscented Kalman Filter to filter the noisy measurements:

// Use the UKF to filter the measurement

ukf.filter(z, dt);

Finally, we update the plot and renderer:

#ifdef VISP_HAVE_DISPLAY
    // Prepare the pose computation:
    // the image points corresponding to the noisy markers are needed
    std::vector<vpImagePoint> ip;
    for (unsigned int id = 0; id < nbMarkers; ++id) {
      vpImagePoint markerProjNoisy(z[2*id + 1], z[2*id]);
      ip.push_back(markerProjNoisy);
    }
 
    // Compute the pose using the noisy markers
    vpHomogeneousMatrix cMo_noisy = computePose(markersAsVpPoint, ip, cam);
    vpHomogeneousMatrix wMo_noisy = cMw.inverse() * cMo_noisy;
    double wXnoisy = wMo_noisy[0][3];
    double wYnoisy = wMo_noisy[1][3];
 
    // Plot the ground truth
    plot.plot(0, 0, object_pos[0], object_pos[1]);
 
    // Plot the filtered state
    vpColVector Xest = ukf.getXest();
    plot.plot(0, 1, Xest[0], Xest[1]);
 
    // Plot the noisy pose
    plot.plot(0, 2, wXnoisy, wYnoisy);
 
    // Display the projection of the markers
    vpDisplay::display(Idisp);
    vpColVector zGT = markerMeas.measureGT(object_pos);
    vpColVector zFilt = markerMeas.state_to_measurement(Xest);
    for (unsigned int id = 0; id < nbMarkers; ++id) {
      vpImagePoint markerProjGT(zGT[2*id + 1], zGT[2*id]);
      vpDisplay::displayCross(Idisp, markerProjGT, 5, vpColor::red);
 
      vpImagePoint markerProjFilt(zFilt[2*id + 1], zFilt[2*id]);
      vpDisplay::displayCross(Idisp, markerProjFilt, 5, vpColor::blue);
 
      vpImagePoint markerProjNoisy(z[2*id + 1], z[2*id]);
      vpDisplay::displayCross(Idisp, markerProjNoisy, 5, vpColor::black);
    }
 
    vpImagePoint ipText(20, 20);
    vpDisplay::displayText(Idisp, ipText, std::string("GT"), vpColor::red);
    ipText.set_i(ipText.get_i() + 20);
    vpDisplay::displayText(Idisp, ipText, std::string("Filtered"), vpColor::blue);
    ipText.set_i(ipText.get_i() + 20);
    vpDisplay::displayText(Idisp, ipText, std::string("Measured"), vpColor::black);
    vpDisplay::flush(Idisp);
    vpTime::wait(40);
#endif

First, we compute the noisy pose using the noisy measurements of the markers, to be able to plot the noisy 3D position of the object:

    // Prepare the pose computation:
    // the image points corresponding to the noisy markers are needed
    std::vector<vpImagePoint> ip;
    for (unsigned int id = 0; id < nbMarkers; ++id) {
      vpImagePoint markerProjNoisy(z[2*id + 1], z[2*id]);
      ip.push_back(markerProjNoisy);
    }
 
    // Compute the pose using the noisy markers
    vpHomogeneousMatrix cMo_noisy = computePose(markersAsVpPoint, ip, cam);
    vpHomogeneousMatrix wMo_noisy = cMw.inverse() * cMo_noisy;
    double wXnoisy = wMo_noisy[0][3];
    double wYnoisy = wMo_noisy[1][3];

Then, we update the plot by plotting the new ground truth, filtered and noisy 3D positions:

    // Plot the ground truth
    plot.plot(0, 0, object_pos[0], object_pos[1]);
 
    // Plot the filtered state
    vpColVector Xest = ukf.getXest();
    plot.plot(0, 1, Xest[0], Xest[1]);
 
    // Plot the noisy pose
    plot.plot(0, 2, wXnoisy, wYnoisy);

Finally, we update the renderer that displays the projection in the image of the markers:

    // Display the projection of the markers
    vpDisplay::display(Idisp);
    vpColVector zGT = markerMeas.measureGT(object_pos);
    vpColVector zFilt = markerMeas.state_to_measurement(Xest);
    for (unsigned int id = 0; id < nbMarkers; ++id) {
      vpImagePoint markerProjGT(zGT[2*id + 1], zGT[2*id]);
      vpDisplay::displayCross(Idisp, markerProjGT, 5, vpColor::red);
 
      vpImagePoint markerProjFilt(zFilt[2*id + 1], zFilt[2*id]);
      vpDisplay::displayCross(Idisp, markerProjFilt, 5, vpColor::blue);
 
      vpImagePoint markerProjNoisy(z[2*id + 1], z[2*id]);
      vpDisplay::displayCross(Idisp, markerProjNoisy, 5, vpColor::black);
    }
 
    vpImagePoint ipText(20, 20);
    vpDisplay::displayText(Idisp, ipText, std::string("GT"), vpColor::red);
    ipText.set_i(ipText.get_i() + 20);
    vpDisplay::displayText(Idisp, ipText, std::string("Filtered"), vpColor::blue);
    ipText.set_i(ipText.get_i() + 20);
    vpDisplay::displayText(Idisp, ipText, std::string("Measured"), vpColor::black);
    vpDisplay::flush(Idisp);
    vpTime::wait(40);

The program stops once the Return key is pressed.

Next tutorial

You are now ready to see the next Tutorial: Using Particle Filter to filter your data.

Table of Contents