Visual Servoing Platform  version 3.6.1 under development (2024-11-21)
Public Types | Public Member Functions | Protected Member Functions | Protected Attributes | List of all members
vpUKSigmaDrawerMerwe Class Reference
core: Core module » Mathematics » Kalman filter

#include <visp3/core/vpUKSigmaDrawerMerwe.h>

+ Inheritance diagram for vpUKSigmaDrawerMerwe:

Public Types

typedef vpUnscentedKalman::vpAddSubFunction vpAddSubFunction
 
typedef struct vpUKSigmaDrawerAbstract::vpSigmaPointsWeights vpSigmaPointsWeights
 

Public Member Functions

 vpUKSigmaDrawerMerwe (const int &n, const double &alpha, const double &beta, const double &kappa, const vpAddSubFunction &resFunc=vpUnscentedKalman::simpleResidual, const vpAddSubFunction &addFunc=vpUnscentedKalman::simpleAdd)
 
virtual ~vpUKSigmaDrawerMerwe ()
 
virtual std::vector< vpColVector > drawSigmaPoints (const vpColVector &mean, const vpMatrix &covariance) override
 
virtual vpSigmaPointsWeights computeWeights () override
 

Protected Member Functions

void computeLambda ()
 

Protected Attributes

double m_alpha
 
double m_beta
 
double m_kappa
 
double m_lambda
 
vpAddSubFunction m_resFunc
 
vpAddSubFunction m_addFunc
 
unsigned int m_n
 

Detailed Description

This class defines a class to draw sigma points following the E. A. Wan and R. van der Merwe's method proposed in [51].

The method has four parameters: $ n $, which is the dimension of the input, and 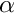$ \alpha $, $ \beta $ and $ \kappa $, which are three reals. For notational convenience, we define $ \lambda = \alpha^2 (n - \kappa) - n $.

Be $ \boldsymbol{\mu} \in {R}^n $ the mean and $ \boldsymbol{\Sigma} \in {R}^{n x n} $ the covariance matrix of the input of the algorithm. The algorithm will draw $ 2n + 1 $ sigma points $ \chi_i \in {R}^n $ such as:

\[ \begin{array}{lcl} \chi_0 &=& \boldsymbol{\mu} \\ \chi_i &=& \begin{cases} \boldsymbol{\mu} + \left[ \sqrt{(n + \lambda) \boldsymbol{\Sigma}} \right]_i^T & i = 1 .. n \\ \boldsymbol{\mu} - \left[ \sqrt{(n + \lambda) \boldsymbol{\Sigma}} \right]_{i - n}^T & i = n + 1 .. 2n \end{cases} \end{array} \]

where the subscript 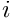$ i $ denotes that we keep the $ i^{th} $ of the matrix.

Several definitions of the square root of a matrix exists. We decided to use the following definition: $ \textbf{L} $ is the square root of the matrix $ \boldsymbol{\Sigma} $ if $ \boldsymbol{\Sigma} $ can be written as:

$ \boldsymbol{\Sigma} = \textbf{L} \textbf{L}^T $

This definition is favored because it can be computed using the Cholesky's decomposition.

The computation of the weights that go along the sigma points is the following. The weight used for the computation of the mean of $ \chi_0 $ is computed such as:

$ w_0^m = \frac{\lambda}{n + \lambda} $

The weight used for the computation of the mean of $ \chi_0 $ is computed such as:

$ w_0^c = \frac{\lambda}{n + \lambda} + 1 - \alpha^2 + \beta $

The weights for the other sigma points $ \chi_1 ... \chi_{2n} $ are the same for the mean and covariance and are computed as follow:

$ w_i^m = w_i^c = \frac{1}{2(n + \lambda)} i = 1..2n $

Note: the weights do not sum to one. Negative values can even be expected.

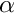Additionnal note: the original author recommended to set $ \beta = 2 $ for Gaussian problems, $ \kappa = 3 - n $ and $ 0 \leq \alpha \leq 1 $, where a larger value for $ \alpha $ spreads the sigma points further from the mean, which can be a problem for highly non-linear problems.

Definition at line 96 of file vpUKSigmaDrawerMerwe.h.

Member Typedef Documentation

◆ vpAddSubFunction

typedef vpUnscentedKalman::vpAddSubFunction vpUKSigmaDrawerMerwe::vpAddSubFunction

Definition at line 99 of file vpUKSigmaDrawerMerwe.h.

◆ vpSigmaPointsWeights

typedef struct vpUKSigmaDrawerAbstract::vpSigmaPointsWeights vpUKSigmaDrawerAbstract::vpSigmaPointsWeights
inherited

The weights corresponding to the sigma points drawing.

Constructor & Destructor Documentation

◆ vpUKSigmaDrawerMerwe()

BEGIN_VISP_NAMESPACE vpUKSigmaDrawerMerwe::vpUKSigmaDrawerMerwe ( const int &  n,
const double &  alpha,
const double &  beta,
const double &  kappa,
const vpAddSubFunction &  resFunc = vpUnscentedKalman::simpleResidual,
const vpAddSubFunction &  addFunc = vpUnscentedKalman::simpleAdd 
)

Construct a new vpUKSigmaDrawerMerwe object.

Parameters
[in]nThe size of the state vector.
[in]alphaA factor, which should be a real in the interval [0; 1]. The larger alpha is, the further the sigma points are spread from the mean.
[in]betaAnother factor, which should be set to 2 if the problem is Gaussian.
[in]kappaA third factor, whose value should be set to 3 - n for most problems.
[in]resFuncResidual function expressed in the state space.
[in]addFuncAddition function expressed in the state space.

Definition at line 45 of file vpUKSigmaDrawerMerwe.cpp.

References computeLambda().

◆ ~vpUKSigmaDrawerMerwe()

virtual vpUKSigmaDrawerMerwe::~vpUKSigmaDrawerMerwe ( )
inlinevirtual

Destructor that does nothing.

Definition at line 119 of file vpUKSigmaDrawerMerwe.h.

Member Function Documentation

◆ computeLambda()

void vpUKSigmaDrawerMerwe::computeLambda ( )
inlineprotected

Definition at line 138 of file vpUKSigmaDrawerMerwe.h.

References vpUKSigmaDrawerAbstract::m_n.

Referenced by vpUKSigmaDrawerMerwe().

◆ computeWeights()

vpUKSigmaDrawerMerwe::vpSigmaPointsWeights vpUKSigmaDrawerMerwe::computeWeights ( )
overridevirtual

Computed the weigths that correspond to the sigma poitns that have been drawn.

Returns
vpSigmaPointsWeights The weights that correspond to the sigma points.

Implements vpUKSigmaDrawerAbstract.

Definition at line 71 of file vpUKSigmaDrawerMerwe.cpp.

References m_alpha, m_beta, m_lambda, vpUKSigmaDrawerAbstract::m_n, vpUKSigmaDrawerAbstract::vpSigmaPointsWeights::m_wc, and vpUKSigmaDrawerAbstract::vpSigmaPointsWeights::m_wm.

◆ drawSigmaPoints()

std::vector< vpColVector > vpUKSigmaDrawerMerwe::drawSigmaPoints ( const vpColVector &  mean,
const vpMatrix &  covariance 
)
overridevirtual

Draw the sigma points according to the current mean and covariance of the state of the Unscented Kalman filter.

Parameters
[in]meanThe current mean of the state of the UKF.
[in]covarianceThe current process covariance of the UKF.
Returns
std::vector<vpColVector> The sigma points.

Implements vpUKSigmaDrawerAbstract.

Definition at line 57 of file vpUKSigmaDrawerMerwe.cpp.

References vpMatrix::cholesky(), vpMatrix::getRow(), m_addFunc, m_lambda, vpUKSigmaDrawerAbstract::m_n, m_resFunc, and vpRowVector::transpose().

Member Data Documentation

◆ m_addFunc

vpAddSubFunction vpUKSigmaDrawerMerwe::m_addFunc
protected

Addition function expressed in the state space.

Definition at line 149 of file vpUKSigmaDrawerMerwe.h.

Referenced by drawSigmaPoints().

◆ m_alpha

double vpUKSigmaDrawerMerwe::m_alpha
protected

A factor, which should be a real in the interval [0; 1]. The larger alpha is, the further the sigma points are spread from the mean.

Definition at line 143 of file vpUKSigmaDrawerMerwe.h.

Referenced by computeWeights().

◆ m_beta

double vpUKSigmaDrawerMerwe::m_beta
protected

Another factor, which should be set to 2 if the problem is Gaussian.

Definition at line 145 of file vpUKSigmaDrawerMerwe.h.

Referenced by computeWeights().

◆ m_kappa

double vpUKSigmaDrawerMerwe::m_kappa
protected

A third factor, whose value should be set to 3 - n for most problems.

Definition at line 146 of file vpUKSigmaDrawerMerwe.h.

◆ m_lambda

double vpUKSigmaDrawerMerwe::m_lambda
protected

$ \alpha^2 (n + \kappa) - n $, where $ n $ is the size of the state vector.

Definition at line 147 of file vpUKSigmaDrawerMerwe.h.

Referenced by computeWeights(), and drawSigmaPoints().

◆ m_n

unsigned int vpUKSigmaDrawerAbstract::m_n
protectedinherited

The size of the state of the UKF.

Definition at line 81 of file vpUKSigmaDrawerAbstract.h.

Referenced by computeLambda(), computeWeights(), and drawSigmaPoints().

◆ m_resFunc

vpAddSubFunction vpUKSigmaDrawerMerwe::m_resFunc
protected

Residual function expressed in the state space.

Definition at line 148 of file vpUKSigmaDrawerMerwe.h.

Referenced by drawSigmaPoints().