Introduction
We suppose that you are already familiar with the Tutorial: Using Unscented Kalman Filter to filter your data.
The Particle Filters (PF) are a set of Monte Carlo algorithms that permit to approximate solutions for filtering problems even when the state-space and/or measurement space are non-linear.
In this tutorial, we will use a PF on the same use-case than presented in Tutorial: Using Unscented Kalman Filter to filter your data. The PF is used to filter the 3D position of a simulated object, which revolves in a plane parallel to the ground around a static point, which is the origin of the world frame 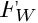 . The coordinate frame attached to the object is denoted
. The coordinate frame attached to the object is denoted 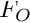 . The object is observed by a static camera whose coordinate frame is denoted
. The object is observed by a static camera whose coordinate frame is denoted 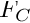 . The object is supposed plane and having four markers sticked on its surface.
. The object is supposed plane and having four markers sticked on its surface.
The equations that describe the motion of the object in the world frame are the following:
![\[ \begin{array}{lcl} {}^W \textbf{X}_x &=& R cos(\omega t + \phi) \\ {}^W \textbf{X}_y &=& R sin(\omega t + \phi) \\ {}^W \textbf{X}_z &=& constant \end{array} \]](form_1736.png)
where 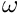 and
and 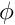 are respectively the pulsation and the phase of the motion, while
are respectively the pulsation and the phase of the motion, while 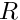 is the radius of the revolution around the origin of the world frame.
is the radius of the revolution around the origin of the world frame.
The maths beyond the Particle Filter
The maths beyond the Particle Filter are explained in the documentation of the vpParticleFilter class. We will recall briefly the important steps of the PF.
Be 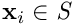 a particle representing the internal state of the PF, with
a particle representing the internal state of the PF, with  and
and 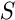 the state space. To each particle is associated a weight
the state space. To each particle is associated a weight 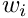 that represents its likelihood knowing the measurements and is used to compute the filtered state
that represents its likelihood knowing the measurements and is used to compute the filtered state 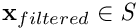 .
.
The first step of the PF is the prediction step. During this step, the particles of the PF are projected forward in time. Be 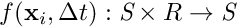 the process function that project the forward in time. All the particles pass through the function , and some noise
the process function that project the forward in time. All the particles pass through the function , and some noise 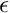 is independently added to each of them to form the new particles:
is independently added to each of them to form the new particles:
![\[ \textbf{x}_i(t + \Delta t) = f( \textbf{x}_i(t) , \Delta t ) + \epsilon \]](form_1621.png)
The second step of the PF is to update the weights 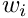 associated to each particle based on new measurements. The update is based on the likelihood of a particle based on the measurements
associated to each particle based on new measurements. The update is based on the likelihood of a particle based on the measurements 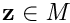 , where
, where 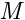 is the measurement space. Be
is the measurement space. Be ![$ l: \textit{S} \times \textit{M} \rightarrow [0; 1.] $](form_1624.png) the likelihood function, we have:
the likelihood function, we have:
![\[ w_i = l(\textbf{x}_i, \textbf{z}) \]](form_1625.png)
After an update, a check is performed to see if the PF is not degenerated (i.e. if the weigths of most particles became very low). If the PF became degenerated, the particles are resampled depending on a resampling scheme. Different kind of checks and of resampling algorithms exist in the litterature.
Finally, we can compute the new state estimate  by performing a weighted mean of the particles
by performing a weighted mean of the particles 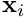 . Be
. Be 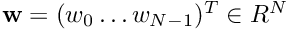 ,
, 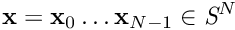 and
and 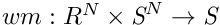 the weighted mean function of the state space
the weighted mean function of the state space 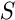 , we have:
, we have:
![\[ \textbf{x}_{filtered} = wm(\textbf{w}, \textbf{x}) \]](form_1631.png)
Explanations about the tutorial
How to run the tutorial
To run the tutorial, please run the following commands:
$ cd $VISP_WS/
visp-build/tutorial/particle-filter
$ ./tutorial-pf
To see the arguments the program can take, please run:
$ cd $VISP_WS/
visp-build/tutorial/particle-filter
$ ./tutorial-pf -h
You should see something similar to the following image:
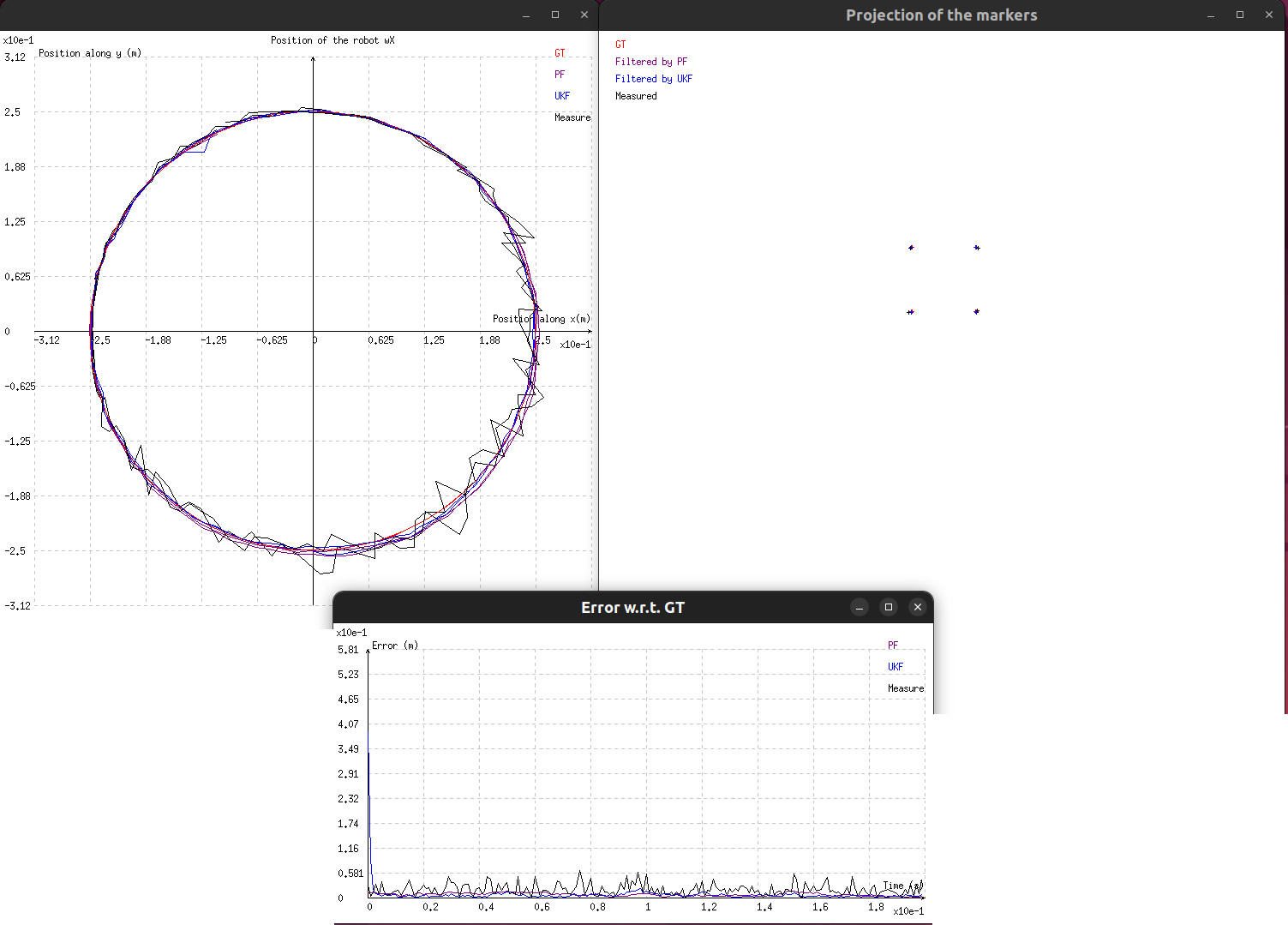
Screenshot of the tutorial Graphical User Interface
Press Return to leave the program.
Detailed explanations about the PF tutorial
For this tutorial, we use the main program tutorial-pf.cpp . An Unscented Kalman Filter (UKF) is also implemented to compare the results of both methods. The internal state of both the PF and the UKF is the 3D position of the object expressed in the world frame, along with the pulsation 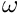 of the motion:
of the motion:
![\[ \begin{array}{lcl} \textbf{x}[0] &=& {}^WX_x \\ \textbf{x}[1] &=& {}^WX_y \\ \textbf{x}[2] &=& {}^WX_z \\ \textbf{x}[3] &=& \omega \Delta t \end{array} \]](form_1719.png)
The measurement 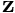 corresponds to the perspective projection of the different markers in the image. Be
corresponds to the perspective projection of the different markers in the image. Be 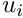 and
and 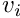 the horizontal and vertical pixel coordinates of the
the horizontal and vertical pixel coordinates of the 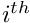 marker. The measurement vector can be written as:
marker. The measurement vector can be written as:
![\[ \begin{array}{lcl} \textbf{z}[2i] &=& u_i \\ \textbf{z}[2i+1] &=& v_i \end{array} \]](form_1722.png)
Be 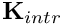 the camera instrinsic parameters matrix defined by:
the camera instrinsic parameters matrix defined by:
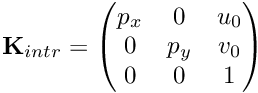
where 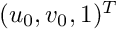 are the coordinates of the principal point and
are the coordinates of the principal point and 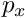 (resp.
(resp. 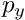 ) is the ratio between the focal lens of the camera and the width (resp. height) of a pixel.
) is the ratio between the focal lens of the camera and the width (resp. height) of a pixel.
Be 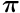 the projection matrix that is, in the case of a perspective projection model, given by:
the projection matrix that is, in the case of a perspective projection model, given by:

The perspective projection 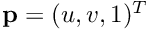 of a point
of a point 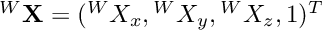 is given by:
is given by:
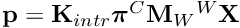
where 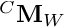 is the homogeneous matrix that expresses the pose of the world coordinate frame
is the homogeneous matrix that expresses the pose of the world coordinate frame 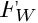 with regard to the camera frame
with regard to the camera frame 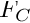 .
.
Details on the includes
To have a Graphical User Interface (GUI), we include the following files.
#ifdef VISP_HAVE_DISPLAY
#include <visp3/gui/vpPlot.h>
#include <visp3/gui/vpDisplayFactory.h>
#endif
To be able to use the PF, we use the following includes:
#include <visp3/core/vpParticleFilter.h>
To be able to use an UKF for comparison purpose, we use the following includes:
#include <visp3/core/vpUKSigmaDrawerMerwe.h>
#include <visp3/core/vpUnscentedKalman.h>
Details on the class simulating a moving object
To make simpler the main loop of the program, we decided to implement a class that will update the 3D position of the object, expressed in the world frame, in a dedicated class.
{
public:
vpObjectSimulator(
const double &R,
const double &w,
const double &phi,
const double &wZ,
const double &stdevRng)
: m_R(R)
, m_w(w)
, m_phi(phi)
, m_wZ(wZ)
, m_rng(stdevRng, 0.)
{ }
{
double tNoisy = (m_w + m_rng())* t + m_phi;
wX[0] = m_R * std::cos(tNoisy);
wX[1] = m_R * std::sin(tNoisy);
wX[2] = m_wZ;
return wX;
}
private:
double m_R;
double m_w;
double m_phi;
const double m_wZ;
};
Implementation of column vector and the associated operations.
Class for generating random number with normal probability density.
vpColVector move(const double &t) const
Move the object to its new position, expressed in the world frame.
vpObjectSimulator(const double &R, const double &w, const double &phi, const double &wZ)
Construct a new vpObjectSimulator object.
Details on the process function
As mentionned in The maths beyond the Particle Filter and The maths beyond the Unscented Kalman Filter, both the PF and the UKF rely on a process function which project forward in time their internal state.
We want to express the internal state projected in the future 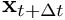 as a function of its previous state
as a function of its previous state 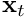 .
.
As stated in the Introduction, the equations of motion of the object are the following:
![\[ \begin{array}{lcl} {}^W X_x(t) &=& R cos(\omega t + \phi) \\ {}^W X_y(t) &=& R sin(\omega t + \phi) \\ {}^W X_z(t) &=& constant \end{array} \]](form_1750.png)
Thus, we have:
![\[ \begin{array}{lclcl} {}^WX_x( t + \Delta t) &=& R cos(\omega (t + \Delta t) + \phi) &=& R cos((\omega t + \phi) + \omega \Delta t )\\ {}^WX_y( t + \Delta t) &=& R sin(\omega (t + \Delta t) + \phi) &=& R sin((\omega t + \phi) + \omega \Delta t )\\ {}^WX_z( t + \Delta t) &=& constant \end{array} \]](form_1751.png)
Which can be rewritten:
![\[ \begin{array}{lclcl} {}^WX_x( t + \Delta t) &=& R cos((\omega t + \phi) + \omega \Delta t ) &=& R cos(\omega t + \phi) cos (\omega \Delta t ) - R sin(\omega t + \phi) sin(\omega \Delta t) \\ {}^WX_y( t + \Delta t) &=& R sin((\omega t + \phi) + \omega \Delta t ) &=& R cos(\omega t + \phi) sin (\omega \Delta t ) + R sin(\omega t + \phi) cos(\omega \Delta t)\\ {}^WX_z( t + \Delta t) &=& constant \end{array} \]](form_1752.png)
And can be finally written as:
![\[ \begin{array}{lclcl} {}^WX_x( t + \Delta t) &=& R cos(\omega t + \phi) cos (\omega \Delta t ) - R sin(\omega t + \phi) sin(\omega \Delta t) &=& {}^W X_x( t) cos(\omega \Delta t) - {}^W X_y(t) sin(\omega \Delta t) \\ {}^WX_y( t + \Delta t) &=& R cos(\omega t + \phi) sin (\omega \Delta t ) + R sin(\omega t + \phi) cos(\omega \Delta t) &=& {}^W X_x( t) sin(\omega \Delta t) + {}^W X_y(t) cos(\omega \Delta t) \\ {}^WX_z( t + \Delta t) &=& constant \end{array} \]](form_1753.png)
This motivates us to choose the following non-linear process function:
![\[ \begin{array}{lclcl} \textbf{x}[0]_{t + \Delta t} &=& {}^WX_x (t + \Delta t) &=& \textbf{x}[0]_{t} cos(\textbf{x}[3]_{t}) - \textbf{x}[1]_{t} sin(\textbf{x}[3]_{t}) \\ \textbf{x}[1]_{t + \Delta t} &=& {}^WX_y (t + \Delta t) &=& \textbf{x}[0]_{t} sin(\textbf{x}[3]_{t}) + \textbf{x}[1]_{t} cos(\textbf{x}[3]_{t}) \\ \textbf{x}[2]_{t + \Delta t} &=& {}^WX_z (t + \Delta t) &=& \textbf{x}[2]_{t} \\ \textbf{x}[3]_{t + \Delta t} &=& \omega \Delta t &=& \textbf{x}[3]_{t} \end{array} \]](form_1754.png)
As the process function is pretty simple, a simple function called here fx() is enough:
{
x_kPlus1[0] = x[0] * std::cos(x[3]) - x[1] * std::sin(x[3]);
x_kPlus1[1] = x[0] * std::sin(x[3]) + x[1] * std::cos(x[3]);
x_kPlus1[2] = x[2];
x_kPlus1[3] = x[3];
return x_kPlus1;
}
Details on the class simulating marker measurement
The measurements of the projection of the markers in the image are handled by the following class:
{
public:
const std::vector<vpColVector> &markers, const double &noise_stdev, const long &seed,
const double &likelihood_stdev)
: m_cam(cam)
, m_cMw(cMw)
, m_wRo(wRo)
, m_markers(markers)
, m_rng(noise_stdev, 0., seed)
{
double sigmaDistanceSquared = likelihood_stdev * likelihood_stdev;
m_constantDenominator = 1. / std::sqrt(2. * M_PI * sigmaDistanceSquared);
m_constantExpDenominator = -1. / (2. * sigmaDistanceSquared);
const unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
for (unsigned int i = 0; i < nbMarkers; ++i) {
m_markersAsVpPoint.push_back(
vpPoint(marker[0], marker[1], marker[2]));
}
}
{
unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
for (unsigned int i = 0; i < nbMarkers; ++i) {
double u = 0., v = 0.;
meas[2*i] = u;
meas[2*i + 1] = v;
}
return meas;
}
{
unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
for (unsigned int i = 0; i < nbMarkers; ++i) {
double u = 0., v = 0.;
meas[2*i] = u;
meas[2*i + 1] = v;
}
return meas;
}
{
unsigned int sizeMeasurement = measurementsGT.
size();
for (unsigned int i = 0; i < sizeMeasurement; ++i) {
measurementsNoisy[i] += m_rng();
}
return measurementsNoisy;
}
{
unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
const unsigned int sizePt2D = 2;
const unsigned int idX = 0, idY = 1, idZ = 2;
double sumError = 0.;
for (unsigned int i = 0; i < nbMarkers; ++i) {
vpImagePoint measPt(meas[sizePt2D * i + 1], meas[sizePt2D * i]);
sumError += error;
}
likelihood = std::exp(m_constantExpDenominator * sumError /
static_cast<double>(nbMarkers)) * m_constantDenominator;
}
private:
std::vector<vpColVector> m_markers;
std::vector<vpPoint> m_markersAsVpPoint;
double m_constantDenominator;
double m_constantExpDenominator;
};
unsigned int size() const
Return the number of elements of the 2D array.
Generic class defining intrinsic camera parameters.
Implementation of an homogeneous matrix and operations on such kind of matrices.
vpHomogeneousMatrix & buildFrom(const vpTranslationVector &t, const vpRotationMatrix &R)
Class that defines a 2D point in an image. This class is useful for image processing and stores only ...
static double sqrDistance(const vpImagePoint &iP1, const vpImagePoint &iP2)
vpColVector state_to_measurement(const vpColVector &x)
[Measurement_function]
double likelihood(const vpColVector &x, const vpColVector &meas)
[Noisy_measurements]
vpMarkersMeasurements(const vpCameraParameters &cam, const vpHomogeneousMatrix &cMw, const vpRotationMatrix &wRo, const std::vector< vpColVector > &markers, const double &noise_stdev, const long &seed)
Construct a new vpMarkersMeasurements object.
vpColVector measureGT(const vpColVector &wX)
[Measurement_function]
vpColVector measureWithNoise(const vpColVector &wX)
[GT_measurements]
static void convertPoint(const vpCameraParameters &cam, const double &x, const double &y, double &u, double &v)
Class that defines a 3D point in the object frame and allows forward projection of a 3D point in the ...
Implementation of a rotation matrix and operations on such kind of matrices.
Class that consider the case of a translation vector.
It takes as input the camera parameters cam, the homogeneous matrix expressing the pose of the world frame 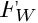 with regard to the camera frame
with regard to the camera frame 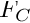
cMw, the rotation matrix that expresses the rotation between the object frame and world frame wRo and the homogeneous coordinates of the markers expressed in the object frame markers to be able to convert the 3D position of the object in the world frame 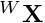 into 3D positions of the markers in the camera frame
into 3D positions of the markers in the camera frame 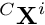 , where
, where 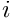 denotes the i
denotes the i 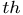 marker sticked on the object. The standard deviation of the noise
marker sticked on the object. The standard deviation of the noise noise_stdev and the seed value seed are here to initialized the Gaussian noise generator used to simulate noisy measurements. Additionally, the likelihood standard deviation 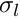 is given for the computation of the likelihood of a PF particle knowing the measurements.
is given for the computation of the likelihood of a PF particle knowing the measurements.
The method state_to_measurement is used to convert the internal state of the UKF into the measurement space (i.e. the projection in the image of the markers sticked on the object if the object is at this 3D position):
{
unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
for (unsigned int i = 0; i < nbMarkers; ++i) {
double u = 0., v = 0.;
meas[2*i] = u;
meas[2*i + 1] = v;
}
return meas;
}
The method measureGT is used to convert the ground truth 3D position of the object into ground truth projections of the markers in the image:
{
unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
for (unsigned int i = 0; i < nbMarkers; ++i) {
double u = 0., v = 0.;
meas[2*i] = u;
meas[2*i + 1] = v;
}
return meas;
}
The method measureWithNoise adds noise to the ground truth measurements in order to simulate a noisy measurement process:
{
unsigned int sizeMeasurement = measurementsGT.
size();
for (unsigned int i = 0; i < sizeMeasurement; ++i) {
measurementsNoisy[i] += m_rng();
}
return measurementsNoisy;
}
The method likelihood computes the likelihood of a particle knowing the measurements. We decided to implement a Gaussian function that penalizes the mean distance between the projection of the markers corresponding to the particle position and the measurements of the markers in the image.
![\[ w_i = l(\textbf{x}_i, \textbf{z}) := \frac{1}{\sqrt{2. * \Pi * \sigma_l^2}} exp^{- \frac{\overline{e}}{2 * \sigma_l^2}} \]](form_1759.png)
where 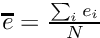 is the mean reprojection error of the markers.
is the mean reprojection error of the markers.
Here is the corresponding code:
{
unsigned int nbMarkers = static_cast<unsigned int>(m_markers.size());
double likelihood = 0.;
const unsigned int sizePt2D = 2;
const unsigned int idX = 0, idY = 1, idZ = 2;
double sumError = 0.;
for (unsigned int i = 0; i < nbMarkers; ++i) {
vpImagePoint measPt(meas[sizePt2D * i + 1], meas[sizePt2D * i]);
sumError += error;
}
likelihood = std::exp(m_constantExpDenominator * sumError / static_cast<double>(nbMarkers)) * m_constantDenominator;
likelihood = std::min(likelihood, 1.0);
likelihood = std::max(likelihood, 0.);
return likelihood;
}
Details on the computation of the pose from noisy measurements
The method computePose compute the 3D pose of an object from the 3D coordinates along with their projection in the image. Here, we use it to convert the noisy measurements in a noisy 3D pose, in order to compare the 3D position estimated by the PF and by the UKF with regard to the 3D position we would have if we computed the pose directly from the noisy measurements.
{
double x = 0, y = 0;
for (unsigned int i = 0; i < point.size(); i++) {
point[i].set_x(x);
point[i].set_y(y);
}
return cMo;
}
static void convertPoint(const vpCameraParameters &cam, const double &u, const double &v, double &x, double &y)
Class used for pose computation from N points (pose from point only). Some of the algorithms implemen...
void addPoint(const vpPoint &P)
@ DEMENTHON_LAGRANGE_VIRTUAL_VS
bool computePose(vpPoseMethodType method, vpHomogeneousMatrix &cMo, FuncCheckValidityPose func=nullptr)
Details on the constants of the main loop
In the main loop of the program, we first declare some constants that will be used later on:
const unsigned int nbIter = 200;
const double dt = 0.001;
const double sigmaMeasurements = 2.;
const double radius = 0.25;
const double w = 2 * M_PI * 10;
const double phi = 2;
const std::vector<vpColVector> markers = {
vpColVector({-0.05, 0.05, 0., 1.}),
const unsigned int nbMarkers = static_cast<unsigned int>(markers.size());
std::vector<vpPoint> markersAsVpPoint;
for (unsigned int i = 0; i < nbMarkers; ++i) {
markersAsVpPoint.push_back(
vpPoint(marker[0], marker[1], marker[2]));
}
const long seed = 42;
cMw[0][0] = 1.; cMw[0][1] = 0.; cMw[0][2] = 0.; cMw[0][3] = 0.2;
cMw[1][0] = 0.; cMw[1][1] = -1.; cMw[1][2] = 0.; cMw[1][3] = 0.3;
cMw[2][0] = 0.; cMw[2][1] = 0.; cMw[2][2] = -1.; cMw[2][3] = 1.;
wMo[0][0] = 1.; wMo[0][1] = 0.; wMo[0][2] = 0.; wMo[0][3] = radius;
wMo[1][0] = 0.; wMo[1][1] = 1.; wMo[1][2] = 0.; wMo[1][3] = 0;
wMo[2][0] = 0.; wMo[2][1] = 0.; wMo[2][2] = 1.; wMo[2][3] = 0.2;
const double wZ = wMo[2][3];
void extract(vpRotationMatrix &R) const
Here is their meanings:
dt is the sampling period (the time spent between two acquisitions), sigmaMeasurements is the standard deviation of the Gaussian noise added to the measurements, radius is the radius of the revolution of the object around the world frame origin, w is the pulsation of the motion of revolution, phi is the phase of the motion of revolution, markers is a vector containing the homogeneous coordinates expressed in the object frame of the markers, markersAsVpPoint is a vector containing the 3D coordinates of the markers expressed in the object (to compute the noisy pose as explained previously), seed is the seed for the Gaussian noise generator that adds noise to the projections of the markers in the image, cMw is the homogeneous matrix expressing the pose of the world frame with regard to the camera frame, wMo is the homogeneous matrix expressing the pose of the object frame with regard to the world frame, wRo is the rotation matrix contained in wMo wZ is the z-axis coordinate of the origin of the object frame expressed in the world frame.
To convert the 3D position of the object into the projection of its markers in the image, we need camera parameters. We generate camera parameters for a simulated camera as follow:
double px = 600; double py = 600; double u0 = 320; double v0 = 240;
void initPersProjWithoutDistortion(double px, double py, double u0, double v0)
Details on the initialization of the PF
To create the particle filter, we need:
- the number of particles
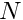 we want to use,
we want to use,
- the standard deviations of each of the components of the state
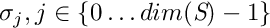 ,
,
- optionnally, the seed to use to create the random noise generators affected to each state components,
- optionnally, the number of threads to use if OpenMP is available.
These parameters can be set using the Command Line Interface (CLI) thanks to the following structure:
{
{ }
int parseArgs(
const int argc,
const char *argv[])
{
int i = 1;
while (i < argc) {
std::string arg(argv[i]);
if ((arg == "--nb-steps-main") && ((i+1) < argc)) {
++i;
}
else if ((arg == "--nb-steps-warmup") && ((i+1) < argc)) {
++i;
}
else if ((arg == "--max-distance-likelihood") && ((i+1) < argc)) {
++i;
}
else if (((arg == "-N") || (arg == "--nb-particles")) && ((i+1) < argc)) {
m_N = std::atoi(argv[i + 1]);
++i;
}
else if ((arg == "--seed") && ((i+1) < argc)) {
++i;
}
else if ((arg == "--nb-threads") && ((i+1) < argc)) {
++i;
}
else if ((arg == "--ampli-max-X") && ((i+1) < argc)) {
++i;
}
else if ((arg == "--ampli-max-Y") && ((i+1) < argc)) {
++i;
}
else if ((arg == "--ampli-max-Z") && ((i+1) < argc)) {
++i;
}
else if ((arg == "--ampli-max-omega") && ((i+1) < argc)) {
++i;
}
else if (arg == "-d") {
}
else if ((arg == "-h") || (arg == "--help")) {
printUsage(std::string(argv[0]));
defaultArgs.printDetails();
return 0;
}
else {
std::cout << "WARNING: unrecognised argument \"" << arg << "\"";
if (i + 1 < argc) {
std::cout << " with associated value(s) { ";
int nbValues = 0;
int j = i + 1;
bool hasToRun = true;
while ((j < argc) && hasToRun) {
std::string nextValue(argv[j]);
if (nextValue.find("--") == std::string::npos) {
std::cout << nextValue << " ";
++nbValues;
}
else {
hasToRun = false;
}
++j;
}
std::cout << "}" << std::endl;
i += nbValues;
}
}
++i;
}
}
private:
void printUsage(const std::string &softName)
{
std::cout << "SYNOPSIS" << std::endl;
std::cout << " " << softName << " [--nb-steps-main <uint>] [--nb-steps-warmup <uint>]" << std::endl;
std::cout << " [--max-distance-likelihood <double>] [-N, --nb-particles <uint>] [--seed <int>] [--nb-threads <int>]" << std::endl;
std::cout << " [--ampli-max-X <double>] [--ampli-max-Y <double>] [--ampli-max-Z <double>] [--ampli-max-omega <double>]" << std::endl;
std::cout << " [-d, --no-display] [-h]" << std::endl;
}
void printDetails()
{
std::cout << std::endl << std::endl;
std::cout << "DETAILS" << std::endl;
std::cout << " --nb-steps-main" << std::endl;
std::cout << " Number of steps in the main loop." << std::endl;
std::cout <<
" Default: " <<
m_nbSteps << std::endl;
std::cout << std::endl;
std::cout << " --nb-steps-warmup" << std::endl;
std::cout << " Number of steps in the warmup loop." << std::endl;
std::cout << std::endl;
std::cout << " --max-distance-likelihood" << std::endl;
std::cout << " Maximum mean distance of the projection of the markers corresponding" << std::endl;
std::cout << " to a particle with the measurements. Above this value, the likelihood of the particle is 0." << std::endl;
std::cout << std::endl;
std::cout << " -N, --nb-particles" << std::endl;
std::cout << " Number of particles of the Particle Filter." << std::endl;
std::cout <<
" Default: " <<
m_N << std::endl;
std::cout << std::endl;
std::cout << " --seed" << std::endl;
std::cout << " Seed to initialize the Particle Filter." << std::endl;
std::cout << " Use a negative value makes to use the current timestamp instead." << std::endl;
std::cout <<
" Default: " <<
m_seedPF << std::endl;
std::cout << std::endl;
std::cout << " --nb-threads" << std::endl;
std::cout << " Set the number of threads to use in the Particle Filter (only if OpenMP is available)." << std::endl;
std::cout << " Use a negative value to use the maximum number of threads instead." << std::endl;
std::cout << std::endl;
std::cout << " --ampli-max-X" << std::endl;
std::cout << " Maximum amplitude of the noise added to a particle along the X-axis." << std::endl;
std::cout << std::endl;
std::cout << " --ampli-max-Y" << std::endl;
std::cout << " Maximum amplitude of the noise added to a particle along the Y-axis." << std::endl;
std::cout << std::endl;
std::cout << " --ampli-max-Z" << std::endl;
std::cout << " Maximum amplitude of the noise added to a particle along the Z-axis." << std::endl;
std::cout << std::endl;
std::cout << " --ampli-max-omega" << std::endl;
std::cout << " Maximum amplitude of the noise added to a particle affecting the pulsation of the motion." << std::endl;
std::cout << std::endl;
std::cout << " -d, --no-display" << std::endl;
std::cout << " Deactivate display." << std::endl;
std::cout << " Default: display is ";
#ifdef VISP_HAVE_DISPLAY
std::cout << "ON" << std::endl;
#else
std::cout << "OFF" << std::endl;
#endif
std::cout << std::endl;
std::cout << " -h, --help" << std::endl;
std::cout << " Display this help." << std::endl;
std::cout << std::endl;
}
};
bool m_useDisplay
If true, activate the plot and the renderer if VISP_HAVE_DISPLAY is defined.
int m_nbThreads
Number of thread to use in the Particle Filter.
unsigned int m_nbSteps
Number of steps for the main loop.
static const int SOFTWARE_CONTINUE
double m_ampliMaxY
Amplitude max of the noise for the state component corresponding to the Y coordinate.
unsigned int m_N
The number of particles.
double m_maxDistanceForLikelihood
The maximum allowed distance between a particle and the measurement, leading to a likelihood equal to...
double m_ampliMaxZ
Amplitude max of the noise for the state component corresponding to the Z coordinate.
int parseArgs(const int argc, const char *argv[])
double m_ampliMaxOmega
Amplitude max of the noise for the state component corresponding to the pulsation.
unsigned int m_nbStepsWarmUp
Number of steps for the warmup phase.
double m_ampliMaxX
Amplitude max of the noise for the state component corresponding to the X coordinate.
long m_seedPF
Seed for the random generators of the PF.
They are thereafter used in the following section of code of the main function:
const double maxDistanceForLikelihood = args.m_maxDistanceForLikelihood;
const double sigmaLikelihood = maxDistanceForLikelihood / 3.;
const unsigned int nbParticles = args.m_N;
const double ampliMaxX = args.m_ampliMaxX, ampliMaxY = args.m_ampliMaxY, ampliMaxZ = args.m_ampliMaxZ;
const double ampliMaxOmega = args.m_ampliMaxOmega;
const std::vector<double> stdevsPF = { ampliMaxX/3., ampliMaxY/3., ampliMaxZ/3., ampliMaxOmega/3. };
long seedPF = args.m_seedPF;
const int nbThread = args.m_nbThreads;
if (seedPF < 0) {
}
VISP_EXPORT double measureTimeMicros()
Then, to initialize the filters, we need:
- a guess of the initial state
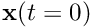 ,
,
- a process function
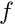 ,
,
- a likelihood function
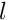 ,
,
- a function that returns true if the filter is degenerated and sampling is needed,
- a function that performs the resampling,
- optionnally, a function to perform the weighted mean
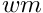 if the addition operation cannot be readily performed in the state space
if the addition operation cannot be readily performed in the state space 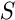 ,
,
- optionnally, a function to perform the addition operation in the state space
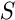 .
.
The section of code corresponding to the declaration of these functions is the following:
using std::placeholders::_1;
using std::placeholders::_2;
The class permits to use a Particle Filter.
std::function< vpParticlesWithWeights(const std::vector< vpColVector > &, const std::vector< double > &)> vpResamplingFunction
Function that takes as argument the vector of particles and the vector of associated weights....
std::function< vpColVector(const vpColVector &, const double &)> vpProcessFunction
Process model function, which projects a particle forward in time. The first argument is a particle,...
std::function< bool(const unsigned int &, const std::vector< double > &)> vpResamplingConditionFunction
Function that takes as argument the number of particles and the vector of weights associated to each ...
std::function< double(const vpColVector &, const MeasurementsType &)> vpLikelihoodFunction
Likelihood function, which evaluates the likelihood of a particle with regard to the measurements....
When both the constants and the functions have been declared, it is possible to create the PF using the following code:
pfFilter.init(X0, processFunc, likelihoodFunc, checkResamplingFunc, resamplingFunc);
Initialization of the UKF, used for comparison purpose
We refer the user to Details on the initialization of the UKF for more detailed explanations on the initialization of the UKF, as this tutorial uses the same use-case. The code corresponding to the creation and initialization of the UKF is the following:
std::shared_ptr<vpUKSigmaDrawerAbstract> drawer = std::make_shared<vpUKSigmaDrawerMerwe>(4, 0.001, 2., -1);
R1landmark[0][0] = sigmaMeasurements*sigmaMeasurements;
R1landmark[1][1] = sigmaMeasurements*sigmaMeasurements;
for (unsigned int i = 0; i < nbMarkers; ++i) {
R.insert(R1landmark, 2*i, 2*i);
}
const double processVariance = 0.000025;
Q = Q * processVariance;
P0.eye(4);
P0[0][0] = 1.;
P0[1][1] = 1.;
P0[2][2] = 1.;
P0[2][2] = 5.;
ukf.init(X0, P0);
Implementation of a matrix and operations on matrices.
std::function< vpColVector(const vpColVector &)> vpMeasurementFunction
Measurement function, which converts the prior points in the measurement space. The argument is a poi...
std::function< vpColVector(const vpColVector &, const double &)> vpProcessFunction
Process model function, which projects the sigma points forward in time. The first argument is a sigm...
Details on the initialization of the Graphical User Interface
If ViSP has been compiled with any of the third-party graphical libraries, we first begin by initializing the plot that will display the object x and y coordinates expressed in the world frame. Then, we initialize a plot that will display the error norm between either one of the filtered positions or the noisy position and the Ground Truth position. The corresponding code is the following:
#ifdef VISP_HAVE_DISPLAY
plot.initGraph(0, 4);
plot.setTitle(0, "Position of the robot wX");
plot.setUnitX(0, "Position along x(m)");
plot.setUnitY(0, "Position along y (m)");
plot.setLegend(0, 0, "GT");
plot.setLegend(0, 1, "PF");
plot.setLegend(0, 2, "UKF");
plot.setLegend(0, 3, "Measure");
plot.initRange(0, -1.25 * radius, 1.25 * radius, -1.25 * radius, 1.25 * radius);
vpPlot plotError(1, 350, 700, 700, 700,
"Error w.r.t. GT");
plotError.initGraph(0, 3);
plotError.setUnitX(0, "Time (s)");
plotError.setUnitY(0, "Error (m)");
plotError.setLegend(0, 0, "PF");
plotError.setLegend(0, 1, "UKF");
plotError.setLegend(0, 2, "Measure");
plotError.initRange(0, 0, nbIter * dt, 0, radius / 2.);
#endif
static const vpColor blue
static const vpColor black
static const vpColor green
This class enables real time drawing of 2D or 3D graphics. An instance of the class open a window whi...
Then, we initialize the simple renderer that displays what the camera sees:
#ifdef VISP_HAVE_DISPLAY
#endif
std::shared_ptr< vpDisplay > createDisplay()
Return a smart pointer vpDisplay specialization if a GUI library is available or nullptr otherwise.
Details on the initialization of the loop
For the initialization of the loop, we initialize an instance of the vpObjectSimulator class that simulates the moving object. Then, we initialize the current ground-truth 3D position of the object expressed in the world frame, which is the frame in which the internal states of both the PF and the UKF are expressed, as a null homogeneous coordinates vector.
Details on the loop
The main loop of the program is the following:
for (unsigned int i = 0; i < nbIter; ++i) {
double t = dt * static_cast<double>(i);
std::cout << "[Timestep" << i << ", t = " << t << "]" << std::endl;
object_pos = object.move(t);
vpColVector z = markerMeas.measureWithNoise(object_pos);
pfFilter.filter(z, dt);
ukf.filter(z, dt);
for (unsigned int i = 0; i < 3; ++i) {
wX_PF[i] = XestPF[i];
wX_UKF[i] = XestUKF[i];
}
std::cout << " [Particle Filter method] " << std::endl;
std::cout <<
" Norm of the error = " << error_PF.
frobeniusNorm() <<
" m^2" << std::endl;
std::cout << " Fitting duration = " << dtPF << " ms" << std::endl;
std::cout << " [Unscented Kalman Filter method] " << std::endl;
std::cout <<
" Norm of the error = " << error_UKF.
frobeniusNorm() <<
" m^2" << std::endl;
std::cout << " Fitting duration = " << dtUKF << " ms" << std::endl;
#ifdef VISP_HAVE_DISPLAY
std::vector<vpImagePoint> ip;
for (unsigned int id = 0; id < nbMarkers; ++id) {
ip.push_back(markerProjNoisy);
}
double wXnoisy = wMo_noisy[0][3];
double wYnoisy = wMo_noisy[1][3];
plot.plot(0, 0, object_pos[0], object_pos[1]);
plot.plot(0, 1, XestPF[0], XestPF[1]);
plot.plot(0, 2, XestUKF[0], XestUKF[1]);
plot.plot(0, 3, wXnoisy, wYnoisy);
vpColVector zFiltUkf = markerMeas.state_to_measurement(XestUKF);
vpColVector zFiltPF = markerMeas.state_to_measurement(XestPF);
for (unsigned int id = 0; id < nbMarkers; ++id) {
vpImagePoint markerProjFiltPF(zFiltPF[2*
id + 1], zFiltPF[2*
id]);
vpImagePoint markerProjFiltUKF(zFiltUkf[2*
id + 1], zFiltUkf[2*
id]);
}
ipText.set_i(ipText.get_i() + 20);
ipText.set_i(ipText.get_i() + 20);
ipText.set_i(ipText.get_i() + 20);
#endif
}
double frobeniusNorm() const
static void display(const vpImage< unsigned char > &I)
static void displayCross(const vpImage< unsigned char > &I, const vpImagePoint &ip, unsigned int size, const vpColor &color, unsigned int thickness=1)
static void flush(const vpImage< unsigned char > &I)
static void displayText(const vpImage< unsigned char > &I, const vpImagePoint &ip, const std::string &s, const vpColor &color)
vpHomogeneousMatrix inverse() const
vpTranslationVector getTranslationVector() const
VISP_EXPORT int wait(double t0, double t)
VISP_EXPORT double measureTimeMs()
First, we update the ground-truth 3D position of the object based on the simulated time using the following line:
object_pos = object.move(t);
Then, we update the measurement by projecting the 3D position of the markers attached to the object in the image and add some noise to the projections using the following line:
vpColVector z = markerMeas.measureWithNoise(object_pos);
Then, we use the Particle Filter to filter the noisy measurements:
Then, we use the Unscented Kalman Filter to filter the noisy measurements to compare the results:
Finally, we update the plot and renderer:
#ifdef VISP_HAVE_DISPLAY
std::vector<vpImagePoint> ip;
for (unsigned int id = 0; id < nbMarkers; ++id) {
ip.push_back(markerProjNoisy);
}
double wXnoisy = wMo_noisy[0][3];
double wYnoisy = wMo_noisy[1][3];
plot.plot(0, 0, object_pos[0], object_pos[1]);
plot.plot(0, 1, XestPF[0], XestPF[1]);
plot.plot(0, 2, XestUKF[0], XestUKF[1]);
plot.plot(0, 3, wXnoisy, wYnoisy);
vpColVector zFiltUkf = markerMeas.state_to_measurement(XestUKF);
vpColVector zFiltPF = markerMeas.state_to_measurement(XestPF);
for (unsigned int id = 0; id < nbMarkers; ++id) {
vpImagePoint markerProjFiltPF(zFiltPF[2*
id + 1], zFiltPF[2*
id]);
vpImagePoint markerProjFiltUKF(zFiltUkf[2*
id + 1], zFiltUkf[2*
id]);
}
ipText.set_i(ipText.get_i() + 20);
ipText.set_i(ipText.get_i() + 20);
ipText.set_i(ipText.get_i() + 20);
#endif
First, we compute the noisy pose using the noisy measurements of the markers, to be able to plot the noisy 3D position of the object:
std::vector<vpImagePoint> ip;
for (unsigned int id = 0; id < nbMarkers; ++id) {
ip.push_back(markerProjNoisy);
}
double wXnoisy = wMo_noisy[0][3];
double wYnoisy = wMo_noisy[1][3];
Then, we update the plot by plotting the new ground truth, filtered and noisy 3D positions:
plot.plot(0, 0, object_pos[0], object_pos[1]);
plot.plot(0, 1, XestPF[0], XestPF[1]);
plot.plot(0, 2, XestUKF[0], XestUKF[1]);
plot.plot(0, 3, wXnoisy, wYnoisy);
Finally, we update the renderer that displays the projection in the image of the markers:
vpColVector zFiltUkf = markerMeas.state_to_measurement(XestUKF);
vpColVector zFiltPF = markerMeas.state_to_measurement(XestPF);
for (unsigned int id = 0; id < nbMarkers; ++id) {
vpImagePoint markerProjFiltPF(zFiltPF[2*
id + 1], zFiltPF[2*
id]);
vpImagePoint markerProjFiltUKF(zFiltUkf[2*
id + 1], zFiltUkf[2*
id]);
}
ipText.set_i(ipText.get_i() + 20);
ipText.set_i(ipText.get_i() + 20);
ipText.set_i(ipText.get_i() + 20);
The program stops once the Return key is pressed.
Next tutorial
You are now ready to see the next Tutorial: Using Particle Filter to model a wire using polynomial interpolation.


![]() . The coordinate frame attached to the object is denoted
. The coordinate frame attached to the object is denoted ![]() . The object is observed by a static camera whose coordinate frame is denoted
. The object is observed by a static camera whose coordinate frame is denoted ![]() . The object is supposed plane and having four markers sticked on its surface.
. The object is supposed plane and having four markers sticked on its surface.![]()
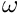 and
and ![]() are respectively the pulsation and the phase of the motion, while
are respectively the pulsation and the phase of the motion, while ![]() is the radius of the revolution around the origin of the world frame.
is the radius of the revolution around the origin of the world frame.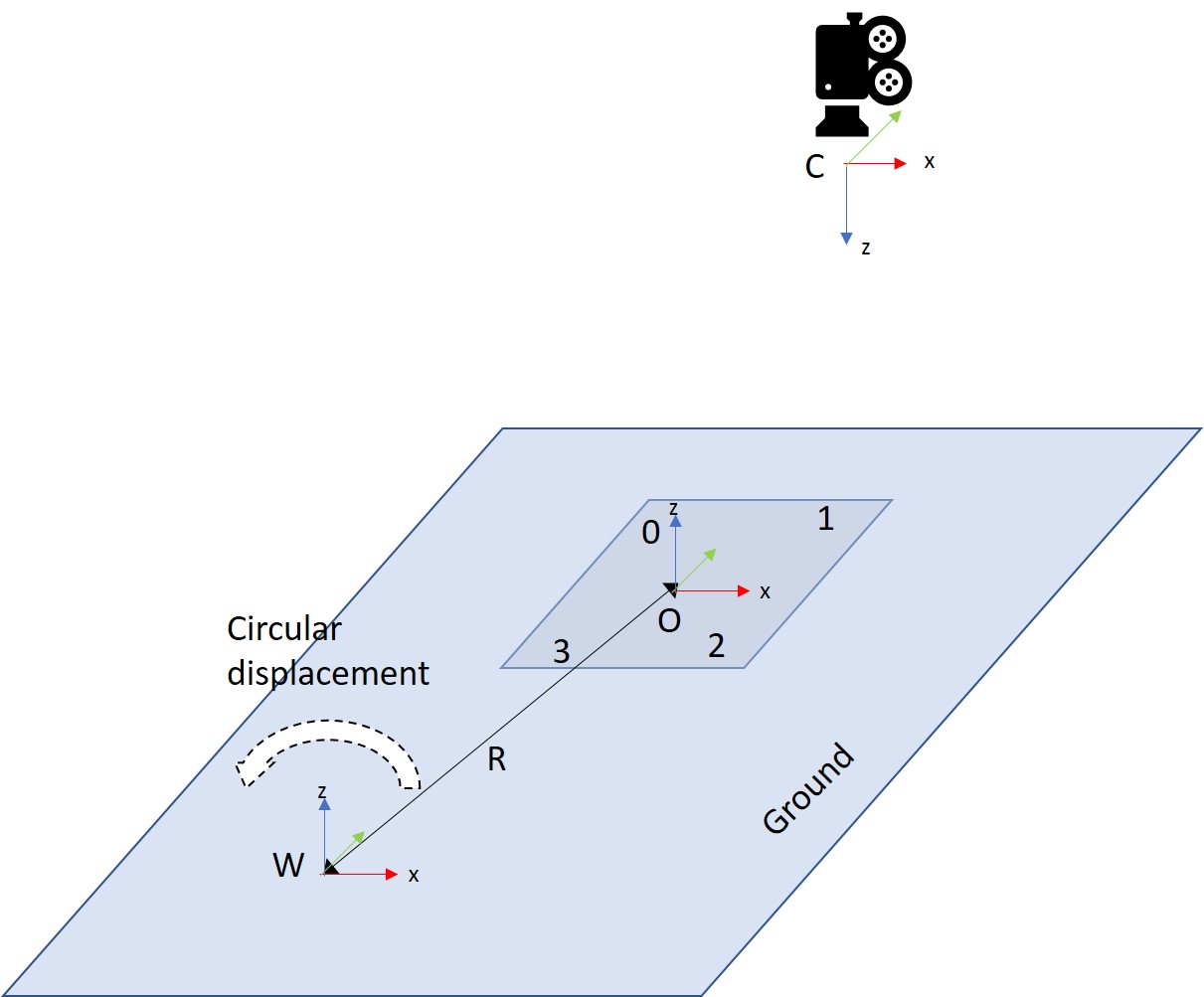
![]() a particle representing the internal state of the PF, with
a particle representing the internal state of the PF, with ![]() and
and ![]() the state space. To each particle is associated a weight
the state space. To each particle is associated a weight ![]() that represents its likelihood knowing the measurements and is used to compute the filtered state
that represents its likelihood knowing the measurements and is used to compute the filtered state ![]() .
.![]() the process function that project the forward in time. All the particles pass through the function , and some noise
the process function that project the forward in time. All the particles pass through the function , and some noise ![]() is independently added to each of them to form the new particles:
is independently added to each of them to form the new particles:![]()
![]() associated to each particle based on new measurements. The update is based on the likelihood of a particle based on the measurements
associated to each particle based on new measurements. The update is based on the likelihood of a particle based on the measurements ![]() , where
, where ![]() is the measurement space. Be
is the measurement space. Be ![]() the likelihood function, we have:
the likelihood function, we have:![]()
![]() by performing a weighted mean of the particles
by performing a weighted mean of the particles ![]() . Be
. Be ![]() ,
, ![]() and
and ![]() the weighted mean function of the state space
the weighted mean function of the state space ![]() , we have:
, we have:![]()

 of the motion:
of the motion:![\[ \begin{array}{lcl} \textbf{x}[0] &=& {}^WX_x \\ \textbf{x}[1] &=& {}^WX_y \\ \textbf{x}[2] &=& {}^WX_z \\ \textbf{x}[3] &=& \omega \Delta t \end{array} \]](form_1719.png)
![]() corresponds to the perspective projection of the different markers in the image. Be
corresponds to the perspective projection of the different markers in the image. Be ![]() and
and ![]() the horizontal and vertical pixel coordinates of the
the horizontal and vertical pixel coordinates of the ![]() marker. The measurement vector can be written as:
marker. The measurement vector can be written as:![]()
![]() the camera instrinsic parameters matrix defined by:
the camera instrinsic parameters matrix defined by:![]()
![]() are the coordinates of the principal point and
are the coordinates of the principal point and ![]() (resp.
(resp. ![]() ) is the ratio between the focal lens of the camera and the width (resp. height) of a pixel.
) is the ratio between the focal lens of the camera and the width (resp. height) of a pixel.![]() the projection matrix that is, in the case of a perspective projection model, given by:
the projection matrix that is, in the case of a perspective projection model, given by:![]()
![]() of a point
of a point ![]() is given by:
is given by:![]()
![]() is the homogeneous matrix that expresses the pose of the world coordinate frame
is the homogeneous matrix that expresses the pose of the world coordinate frame ![]() with regard to the camera frame
with regard to the camera frame ![]() .
.![]() as a function of its previous state
as a function of its previous state ![]() .
.![]()
![]()
![]()
![]()
![\[ \begin{array}{lclcl} \textbf{x}[0]_{t + \Delta t} &=& {}^WX_x (t + \Delta t) &=& \textbf{x}[0]_{t} cos(\textbf{x}[3]_{t}) - \textbf{x}[1]_{t} sin(\textbf{x}[3]_{t}) \\ \textbf{x}[1]_{t + \Delta t} &=& {}^WX_y (t + \Delta t) &=& \textbf{x}[0]_{t} sin(\textbf{x}[3]_{t}) + \textbf{x}[1]_{t} cos(\textbf{x}[3]_{t}) \\ \textbf{x}[2]_{t + \Delta t} &=& {}^WX_z (t + \Delta t) &=& \textbf{x}[2]_{t} \\ \textbf{x}[3]_{t + \Delta t} &=& \omega \Delta t &=& \textbf{x}[3]_{t} \end{array} \]](form_1754.png)
![]() with regard to the camera frame
with regard to the camera frame ![]()
![]() into 3D positions of the markers in the camera frame
into 3D positions of the markers in the camera frame ![]() , where
, where  denotes the i
denotes the i ![]() marker sticked on the object. The standard deviation of the noise
marker sticked on the object. The standard deviation of the noise ![]() is given for the computation of the likelihood of a PF particle knowing the measurements.
is given for the computation of the likelihood of a PF particle knowing the measurements.![]()
![]() is the mean reprojection error of the markers.
is the mean reprojection error of the markers.