 |
Visual Servoing Platform
version 3.4.0
|
 |
Visual Servoing Platform
version 3.4.0
|
#include <vpMatrix.h>
 Inheritance diagram for vpMatrix:
Inheritance diagram for vpMatrix:Public Types | |
| enum | vpDetMethod { LU_DECOMPOSITION } |
Public Member Functions | |
| vpMatrix () | |
| vpMatrix (unsigned int r, unsigned int c) | |
| vpMatrix (unsigned int r, unsigned int c, double val) | |
| vpMatrix (const vpMatrix &M, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) | |
| vpMatrix (const vpArray2D< double > &A) | |
| vpMatrix (const vpMatrix &A) | |
| vpMatrix (vpMatrix &&A) | |
| vpMatrix (const std::initializer_list< double > &list) | |
| vpMatrix (unsigned int nrows, unsigned int ncols, const std::initializer_list< double > &list) | |
| vpMatrix (const std::initializer_list< std::initializer_list< double > > &lists) | |
| virtual | ~vpMatrix () |
| void | clear () |
Setting a diagonal matrix | |
| void | diag (const double &val=1.0) |
| void | diag (const vpColVector &A) |
| void | eye () |
| void | eye (unsigned int n) |
| void | eye (unsigned int m, unsigned int n) |
Assignment operators | |
| vpMatrix & | operator<< (double *) |
| vpMatrix & | operator<< (double val) |
| vpMatrix & | operator, (double val) |
| vpMatrix & | operator= (const vpArray2D< double > &A) |
| vpMatrix & | operator= (const vpMatrix &A) |
| vpMatrix & | operator= (vpMatrix &&A) |
| vpMatrix & | operator= (const std::initializer_list< double > &list) |
| vpMatrix & | operator= (const std::initializer_list< std::initializer_list< double > > &lists) |
| vpMatrix & | operator= (double x) |
Stacking | |
| void | stack (const vpMatrix &A) |
| void | stack (const vpRowVector &r) |
| void | stack (const vpColVector &c) |
| void | stackColumns (vpColVector &out) |
| vpColVector | stackColumns () |
| void | stackRows (vpRowVector &out) |
| vpRowVector | stackRows () |
Matrix insertion | |
| void | insert (const vpMatrix &A, unsigned int r, unsigned int c) |
Columns, rows, sub-matrices extraction | |
| vpMatrix | extract (unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) const |
| vpColVector | getCol (unsigned int j) const |
| vpColVector | getCol (unsigned int j, unsigned int i_begin, unsigned int size) const |
| vpRowVector | getRow (unsigned int i) const |
| vpRowVector | getRow (unsigned int i, unsigned int j_begin, unsigned int size) const |
| vpColVector | getDiag () const |
| void | init (const vpMatrix &M, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) |
Matrix operations | |
| double | det (vpDetMethod method=LU_DECOMPOSITION) const |
| double | detByLU () const |
| double | detByLUEigen3 () const |
| double | detByLULapack () const |
| double | detByLUOpenCV () const |
| vpMatrix | expm () const |
| vpMatrix & | operator+= (const vpMatrix &B) |
| vpMatrix & | operator-= (const vpMatrix &B) |
| vpMatrix | operator* (const vpMatrix &B) const |
| vpMatrix | operator* (const vpRotationMatrix &R) const |
| vpMatrix | operator* (const vpHomogeneousMatrix &R) const |
| vpMatrix | operator* (const vpVelocityTwistMatrix &V) const |
| vpMatrix | operator* (const vpForceTwistMatrix &V) const |
| vpTranslationVector | operator* (const vpTranslationVector &tv) const |
| vpColVector | operator* (const vpColVector &v) const |
| vpMatrix | operator+ (const vpMatrix &B) const |
| vpMatrix | operator- (const vpMatrix &B) const |
| vpMatrix | operator- () const |
| vpMatrix & | operator+= (double x) |
| vpMatrix & | operator-= (double x) |
| vpMatrix & | operator*= (double x) |
| vpMatrix & | operator/= (double x) |
| vpMatrix | operator* (double x) const |
| vpMatrix | operator/ (double x) const |
| double | sum () const |
| double | sumSquare () const |
Hadamard product | |
| vpMatrix | hadamard (const vpMatrix &m) const |
Kronecker product | |
| void | kron (const vpMatrix &m1, vpMatrix &out) const |
| vpMatrix | kron (const vpMatrix &m1) const |
Transpose | |
| vpMatrix | t () const |
| vpMatrix | transpose () const |
| void | transpose (vpMatrix &At) const |
| vpMatrix | AAt () const |
| void | AAt (vpMatrix &B) const |
| vpMatrix | AtA () const |
| void | AtA (vpMatrix &B) const |
Matrix inversion | |
| vpMatrix | inverseByLU () const |
| vpMatrix | inverseByLUEigen3 () const |
| vpMatrix | inverseByLULapack () const |
| vpMatrix | inverseByLUOpenCV () const |
| vpMatrix | inverseByCholesky () const |
| vpMatrix | inverseByCholeskyLapack () const |
| vpMatrix | inverseByCholeskyOpenCV () const |
| vpMatrix | inverseByQR () const |
| vpMatrix | inverseByQRLapack () const |
| vpMatrix | inverseTriangular (bool upper=true) const |
| vpMatrix | pseudoInverse (double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverse (int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseLapack (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseLapack (int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseEigen3 (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseEigen3 (int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseOpenCV (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseOpenCV (int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
SVD decomposition | |
| double | cond (double svThreshold=1e-6) const |
| unsigned int | kernel (vpMatrix &kerAt, double svThreshold=1e-6) const |
| unsigned int | nullSpace (vpMatrix &kerA, double svThreshold=1e-6) const |
| unsigned int | nullSpace (vpMatrix &kerA, int dim) const |
| void | solveBySVD (const vpColVector &B, vpColVector &x) const |
| vpColVector | solveBySVD (const vpColVector &B) const |
| void | svd (vpColVector &w, vpMatrix &V) |
| void | svdEigen3 (vpColVector &w, vpMatrix &V) |
| void | svdLapack (vpColVector &w, vpMatrix &V) |
| void | svdOpenCV (vpColVector &w, vpMatrix &V) |
QR decomposition | |
| unsigned int | qr (vpMatrix &Q, vpMatrix &R, bool full=false, bool squareR=false, double tol=1e-6) const |
| unsigned int | qrPivot (vpMatrix &Q, vpMatrix &R, vpMatrix &P, bool full=false, bool squareR=false, double tol=1e-6) const |
| void | solveByQR (const vpColVector &b, vpColVector &x) const |
| vpColVector | solveByQR (const vpColVector &b) const |
Eigen values | |
| vpColVector | eigenValues () const |
| void | eigenValues (vpColVector &evalue, vpMatrix &evector) const |
Norms | |
| double | euclideanNorm () const |
| double | frobeniusNorm () const |
| double | inducedL2Norm () const |
| double | infinityNorm () const |
Printing | |
| std::ostream & | cppPrint (std::ostream &os, const std::string &matrixName="A", bool octet=false) const |
| std::ostream & | csvPrint (std::ostream &os) const |
| std::ostream & | maplePrint (std::ostream &os) const |
| std::ostream & | matlabPrint (std::ostream &os) const |
| int | print (std::ostream &s, unsigned int length, const std::string &intro="") const |
| void | printSize () const |
Inherited functionalities from vpArray2D | |
| unsigned int | getCols () const |
| double | getMaxValue () const |
| double | getMinValue () const |
| unsigned int | getRows () const |
| unsigned int | size () const |
| void | resize (unsigned int nrows, unsigned int ncols, bool flagNullify=true, bool recopy_=true) |
| void | reshape (unsigned int nrows, unsigned int ncols) |
| bool | operator== (const vpArray2D< double > &A) const |
| bool | operator!= (const vpArray2D< double > &A) const |
| double * | operator[] (unsigned int i) |
| double * | operator[] (unsigned int i) const |
| vpArray2D< double > | hadamard (const vpArray2D< double > &m) const |
Static Public Member Functions | |
Linear algebra optimization | |
| static unsigned int | getLapackMatrixMinSize () |
| static void | setLapackMatrixMinSize (unsigned int min_size) |
Setting a diagonal matrix with Static Public Member Functions | |
| static void | createDiagonalMatrix (const vpColVector &A, vpMatrix &DA) |
Matrix insertion with Static Public Member Functions | |
| static vpMatrix | insert (const vpMatrix &A, const vpMatrix &B, unsigned int r, unsigned int c) |
| static void | insert (const vpMatrix &A, const vpMatrix &B, vpMatrix &C, unsigned int r, unsigned int c) |
Stacking with Static Public Member Functions | |
| static vpMatrix | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B) |
| static void | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static vpMatrix | stack (const vpMatrix &A, const vpMatrix &B) |
| static vpMatrix | stack (const vpMatrix &A, const vpRowVector &r) |
| static vpMatrix | stack (const vpMatrix &A, const vpColVector &c) |
| static void | stack (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | stack (const vpMatrix &A, const vpRowVector &r, vpMatrix &C) |
| static void | stack (const vpMatrix &A, const vpColVector &c, vpMatrix &C) |
Matrix operations with Static Public Member Functions | |
| static void | add2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | add2Matrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
| static void | add2WeightedMatrices (const vpMatrix &A, const double &wA, const vpMatrix &B, const double &wB, vpMatrix &C) |
| static void | computeHLM (const vpMatrix &H, const double &alpha, vpMatrix &HLM) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpRotationMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpHomogeneousMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpColVector &B, vpColVector &C) |
| static void | multMatrixVector (const vpMatrix &A, const vpColVector &v, vpColVector &w) |
| static void | negateMatrix (const vpMatrix &A, vpMatrix &C) |
| static void | sub2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | sub2Matrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
Kronecker product with Static Public Member Functions | |
| static void | kron (const vpMatrix &m1, const vpMatrix &m2, vpMatrix &out) |
| static vpMatrix | kron (const vpMatrix &m1, const vpMatrix &m2) |
2D Convolution with Static Public Member Functions | |
| static vpMatrix | conv2 (const vpMatrix &M, const vpMatrix &kernel, const std::string &mode="full") |
| static void | conv2 (const vpMatrix &M, const vpMatrix &kernel, vpMatrix &res, const std::string &mode="full") |
Covariance computation with Static Public Member Functions | |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b) |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b, const vpMatrix &w) |
| static vpMatrix | computeCovarianceMatrixVVS (const vpHomogeneousMatrix &cMo, const vpColVector &deltaS, const vpMatrix &Ls, const vpMatrix &W) |
| static vpMatrix | computeCovarianceMatrixVVS (const vpHomogeneousMatrix &cMo, const vpColVector &deltaS, const vpMatrix &Ls) |
Matrix I/O with Static Public Member Functions | |
| static bool | loadMatrix (const std::string &filename, vpArray2D< double > &M, bool binary=false, char *header=NULL) |
| static bool | loadMatrixYAML (const std::string &filename, vpArray2D< double > &M, char *header=NULL) |
| static bool | saveMatrix (const std::string &filename, const vpArray2D< double > &M, bool binary=false, const char *header="") |
| static bool | saveMatrixYAML (const std::string &filename, const vpArray2D< double > &M, const char *header="") |
Inherited I/O from vpArray2D with Static Public Member Functions | |
| static bool | load (const std::string &filename, vpArray2D< double > &A, bool binary=false, char *header=NULL) |
| static bool | loadYAML (const std::string &filename, vpArray2D< double > &A, char *header=NULL) |
| static bool | save (const std::string &filename, const vpArray2D< double > &A, bool binary=false, const char *header="") |
| static bool | saveYAML (const std::string &filename, const vpArray2D< double > &A, const char *header="") |
Public Attributes | |
| double * | data |
Protected Attributes | |
| unsigned int | rowNum |
| unsigned int | colNum |
| double ** | rowPtrs |
| unsigned int | dsize |
Related Functions | |
(Note that these are not member functions.) | |
| vpMatrix | operator* (const double &x, const vpMatrix &B) |
| enum | vpGEMMmethod |
Deprecated functions | |
| vp_deprecated void | init () |
| vp_deprecated void | stackMatrices (const vpMatrix &A) |
| vp_deprecated void | setIdentity (const double &val=1.0) |
| vp_deprecated vpRowVector | row (unsigned int i) |
| vp_deprecated vpColVector | column (unsigned int j) |
| static vp_deprecated vpMatrix | stackMatrices (const vpMatrix &A, const vpMatrix &B) |
| static vp_deprecated void | stackMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static vp_deprecated vpMatrix | stackMatrices (const vpMatrix &A, const vpRowVector &B) |
| static vp_deprecated void | stackMatrices (const vpMatrix &A, const vpRowVector &B, vpMatrix &C) |
| static vp_deprecated vpMatrix | stackMatrices (const vpColVector &A, const vpColVector &B) |
| static vp_deprecated void | stackMatrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
Implementation of a matrix and operations on matrices.
This class needs one of the following third-party to compute matrix inverse, pseudo-inverse, singular value decomposition, determinant:
vpMatrix class provides a data structure for the matrices as well as a set of operations on these matrices.
The vpMatrix class is derived from vpArray2D<double>.
The code below shows how to create a 2-by-3 matrix of doubles, set the element values and access them:
Once build, this previous code produces the following output:
If ViSP is build with c++11 enabled, you can do the same using:
You can also create and initialize a matrix this way:
The Matrix could also be initialized using operator=(const std::initializer_list< std::initializer_list< double > > &)
Definition at line 153 of file vpMatrix.h.
Method used to compute the determinant of a square matrix.
| Enumerator | |
|---|---|
| LU_DECOMPOSITION |
LU decomposition method. |
Definition at line 160 of file vpMatrix.h.
|
inline |
Basic constructor of a matrix of double. Number of columns and rows are zero.
Definition at line 169 of file vpMatrix.h.
|
inline |
Constructor that initialize a matrix of double with 0.
| r | : Matrix number of rows. |
| c | : Matrix number of columns. |
Definition at line 177 of file vpMatrix.h.
|
inline |
Constructor that initialize a matrix of double with val.
| r | : Matrix number of rows. |
| c | : Matrix number of columns. |
| val | : Each element of the matrix is set to val. |
Definition at line 186 of file vpMatrix.h.
| vpMatrix::vpMatrix | ( | const vpMatrix & | M, |
| unsigned int | r, | ||
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) |
Construct a matrix as a sub-matrix of the input matrix M.
Definition at line 189 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, init(), and vpArray2D< Type >::rowNum.
|
inline |
Create a matrix from a 2D array that could be one of the following container that inherit from vpArray2D such as vpMatrix, vpRotationMatrix, vpHomogeneousMatrix, vpPoseVector, vpColVector, vpRowVector...
The following example shows how to create a matrix from an homogeneous matrix:
Definition at line 201 of file vpMatrix.h.
|
inline |
Definition at line 203 of file vpMatrix.h.
| vpMatrix::vpMatrix | ( | vpMatrix && | A | ) |
Definition at line 204 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< double >::dsize, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
|
explicit |
Construct a matrix from a list of double values.
| list | : List of double. |
The following code shows how to use this constructor to initialize a 2-by-3 matrix using reshape() function:
It produces the following output:
Definition at line 244 of file vpMatrix.cpp.
|
explicit |
Construct a matrix from a list of double values.
| ncols,nrows | : Matrix size. |
| list | : List of double. |
The following code shows how to use this constructor to initialize a 2-by-3 matrix:
It produces the following output:
Definition at line 271 of file vpMatrix.cpp.
|
explicit |
Construct a matrix from a list of double values.
| lists | : List of double. The following code shows how to use this constructor to initialize a 2-by-3 matrix function: #include <visp3/core/vpMatrix.h> int main() { #if (VISP_CXX_STANDARD >= VISP_CXX_STANDARD_11) vpMatrix M( { {-1, -2, -3}, {4, 5.5, 6} } ); std::cout << "M:\n" << M << std::endl; #endif } M: -1 -2 -3 4 5.5 6 |
Definition at line 296 of file vpMatrix.cpp.
|
inlinevirtual |
Destructor (Memory de-allocation)
Definition at line 213 of file vpMatrix.h.
| vpMatrix vpMatrix::AAt | ( | ) | const |
Computes the 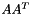 operation
operation 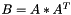
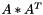
Definition at line 507 of file vpMatrix.cpp.
Referenced by vpServo::computeControlLaw(), and vpServo::computeProjectionOperators().
| void vpMatrix::AAt | ( | vpMatrix & | B | ) | const |
Compute the AAt operation such as 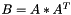 .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 527 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, vpArray2D< Type >::rowNum, and vpArray2D< double >::rowPtrs.
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1352 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator+().
|
static |
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new vector won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1385 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
|
static |
Operation C = A*wA + B*wB
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 1323 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
| vpMatrix vpMatrix::AtA | ( | ) | const |
Compute the AtA operation such as 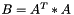
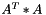
Definition at line 629 of file vpMatrix.cpp.
Referenced by vpServo::computeProjectionOperators(), vpMbDepthDenseTracker::computeVVS(), vpMbDepthNormalTracker::computeVVS(), vpMbGenericTracker::computeVVS(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpMbTracker::computeVVSPoseEstimation(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpNurbs::globalCurveApprox(), vpMbGenericTracker::track(), and vpTemplateTrackerWarp::warp().
| void vpMatrix::AtA | ( | vpMatrix & | B | ) | const |
Compute the AtA operation such as 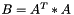 .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 579 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< Type >::rowNum.
|
inline |
Removes all elements from the matrix (which are destroyed), leaving the container with a size of 0.
Definition at line 219 of file vpMatrix.h.
Referenced by vpPose::init().
| vpColVector vpMatrix::column | ( | unsigned int | j | ) |
should be replaced with:
| j | : Index of the column to extract noting that column index start at 1 to get the first column. |
Definition at line 6963 of file vpMatrix.cpp.
References vpArray2D< double >::getRows().
|
static |
Compute the covariance matrix of the parameters x from a least squares minimisation defined as: Ax = b
| A | : Matrix A from Ax = b. |
| x | : Vector x from Ax = b corresponding to the parameters to estimate. |
| b | : Vector b from Ax = b. |
Definition at line 59 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), pseudoInverse(), and t().
Referenced by computeCovarianceMatrixVVS(), vpPoseFeatures::computePose(), and vpPose::poseVirtualVSrobust().
|
static |
Compute the covariance matrix of the parameters x from a least squares minimisation defined as: WAx = Wb
| A | : Matrix A from WAx = Wb. |
| x | : Vector x from WAx = Wb corresponding to the parameters to estimate. |
| b | : Vector b from WAx = Wb. |
| W | : Diagonal weigths matrix from WAx = Wb. |
Definition at line 91 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpArray2D< Type >::getCols(), and t().
|
static |
Compute the covariance matrix of an image-based virtual visual servoing. This assumes the optimization has been done via v = (W * Ls).pseudoInverse() W * DeltaS.
| cMo | : Pose matrix that has been computed with the v. |
| deltaS | : Error vector used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
| Ls | : interaction matrix used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
| W | : Weight matrix used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
Definition at line 149 of file vpMatrix_covariance.cpp.
References computeCovarianceMatrix(), vpHomogeneousMatrix::extract(), eye(), vpArray2D< Type >::getRows(), pseudoInverse(), vpMath::sinc(), vpTranslationVector::skew(), vpColVector::skew(), vpMath::sqr(), and vpColVector::sumSquare().
Referenced by computeCovarianceMatrixVVS(), vpMbTracker::computeCovarianceMatrixVVS(), and vpPose::poseVirtualVS().
|
static |
Compute the covariance matrix of an image-based virtual visual servoing. This assumes the optimization has been done via v = Ls.pseudoInverse() * DeltaS.
| cMo | : Pose matrix that has been computed with the v. |
| deltaS | : Error vector used in v = Ls.pseudoInverse() * DeltaS |
| Ls | : interaction matrix used in v = Ls.pseudoInverse() * DeltaS |
Definition at line 124 of file vpMatrix_covariance.cpp.
References computeCovarianceMatrix(), and computeCovarianceMatrixVVS().
Compute 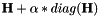
| H | : input Matrix 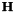 . This matrix should be square. . This matrix should be square. |
| alpha | : Scalar 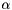 |
| HLM | : Resulting operation. |
Definition at line 6684 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
Referenced by vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerSSDESM::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerMIForwardCompositional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTrackerMIForwardAdditional::initHessienDesired(), vpTemplateTrackerMIESM::initHessienDesired(), vpTemplateTrackerMIInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), vpTemplateTrackerSSDESM::trackNoPyr(), vpTemplateTrackerSSDForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIInverseCompositional::trackNoPyr(), and vpTemplateTrackerWarp::warp().
| double vpMatrix::cond | ( | double | svThreshold = 1e-6 | ) | const |
| svThreshold | Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Definition at line 6623 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpArray2D< Type >::resize(), vpColVector::resize(), and svd().
Referenced by vpTemplateTrackerMIForwardCompositional::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIESM::trackNoPyr(), and vpTemplateTrackerMIInverseCompositional::trackNoPyr().
|
static |
Perform a 2D convolution similar to Matlab conv2 function: 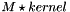 .
.
| M | : First matrix. |
| kernel | : Second matrix. |
| mode | : Convolution mode: "full" (default), "same", "valid". |
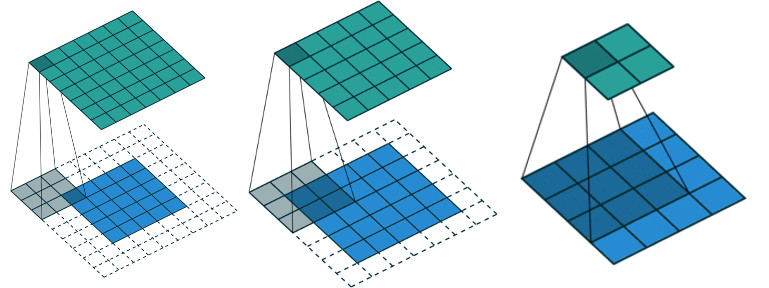
Definition at line 6811 of file vpMatrix.cpp.
Referenced by vpImageFilter::getSobelKernelY().
|
static |
Perform a 2D convolution similar to Matlab conv2 function: 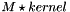 .
.
| M | : First matrix. |
| kernel | : Second matrix. |
| res | : Result. |
| mode | : Convolution mode: "full" (default), "same", "valid". |

Definition at line 6830 of file vpMatrix.cpp.
References vpArray2D< Type >::data, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), and vpArray2D< Type >::resize().
| std::ostream & vpMatrix::cppPrint | ( | std::ostream & | os, |
| const std::string & | matrixName = "A", |
||
| bool | octet = false |
||
| ) | const |
Print to be used as part of a C++ code later.
| os | : the stream to be printed in. |
| matrixName | : name of the matrix, "A" by default. |
| octet | : if false, print using double, if true, print byte per byte each bytes of the double array. |
The following code shows how to use this function:
It produces the following output that could be copy/paste in a C++ code:
Definition at line 5855 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
Referenced by vpColVector::clear().
|
static |
Create a diagonal matrix with the element of a vector 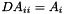 .
.
| A | : Vector which element will be put in the diagonal. |
| DA | : Diagonal matrix DA[i][i] = A[i] |
Definition at line 906 of file vpMatrix.cpp.
References vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
| std::ostream & vpMatrix::csvPrint | ( | std::ostream & | os | ) | const |
Print/save a matrix in csv format.
The following code
produces log.csv file that contains:
Definition at line 5806 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
Referenced by vpColVector::clear().
| double vpMatrix::det | ( | vpDetMethod | method = LU_DECOMPOSITION | ) | const |
Compute the determinant of a n-by-n matrix.
| method | : Method used to compute the determinant. Default LU decomposition method is faster than the method based on Gaussian elimination. |
Definition at line 6477 of file vpMatrix.cpp.
References detByLU(), and LU_DECOMPOSITION.
Referenced by vpTriangle::buildFrom(), vpHomography::computeDisplacement(), detByLULapack(), detByLUOpenCV(), vpTemplateTrackerTriangle::init(), and inverseByLU().
| double vpMatrix::detByLU | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition.
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default detByLULapack() with a Lapack built-in version.
Definition at line 224 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, detByLUEigen3(), detByLULapack(), detByLUOpenCV(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by det().
| double vpMatrix::detByLUEigen3 | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition with Eigen3 3rd party.
Definition at line 614 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< double >::rowNum.
Referenced by detByLU().
| double vpMatrix::detByLULapack | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition with Lapack 3rd party.
Definition at line 378 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, det(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by detByLU().
| double vpMatrix::detByLUOpenCV | ( | ) | const |
Compute the determinant of a n-by-n matrix using the LU decomposition with OpenCV 3rd party.
Definition at line 524 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, det(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by detByLU().
| void vpMatrix::diag | ( | const double & | val = 1.0 | ) |
Set the matrix as a diagonal matrix where each element on the diagonal is set to val. Elements that are not on the diagonal are set to 0.
| val | : Value to set. |
Matrix A is now equal to:
Definition at line 887 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by vpMbTracker::computeCovarianceMatrixVVS(), vpQuadProg::fromCanonicalCost(), and getDiag().
| void vpMatrix::diag | ( | const vpColVector & | A | ) |
Create a diagonal matrix with the element of a vector.
| A | : Vector which element will be put in the diagonal. |
Matrix A is now equal to:
Definition at line 847 of file vpMatrix.cpp.
References vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpColVector vpMatrix::eigenValues | ( | ) | const |
Compute the eigenvalues of a n-by-n real symmetric matrix using Lapack 3rd party.
| vpException::dimensionError | If the matrix is not square. |
| vpException::fatalError | If the matrix is not symmetric. |
| vpException::functionNotImplementedError | If the Lapack 3rd party is not detected. |
Here an example:
Definition at line 6040 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpException::functionNotImplementedError, vpColVector::resize(), vpArray2D< double >::rowNum, and t().
Referenced by vpQuadProg::fromCanonicalCost(), and vpMath::lineFitting().
| void vpMatrix::eigenValues | ( | vpColVector & | evalue, |
| vpMatrix & | evector | ||
| ) | const |
Compute the eigenvalues of a n-by-n real symmetric matrix using Lapack 3rd party.
| evalue | : Eigenvalues of the matrix, sorted in ascending order. |
| evector | : Corresponding eigenvectors of the matrix. |
| vpException::dimensionError | If the matrix is not square. |
| vpException::fatalError | If the matrix is not symmetric. |
| vpException::functionNotImplementedError | If Lapack 3rd party is not detected. |
Here an example:
Definition at line 6164 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpException::functionNotImplementedError, vpArray2D< Type >::resize(), vpColVector::resize(), vpArray2D< double >::rowNum, and t().
| vp_deprecated double vpMatrix::euclideanNorm | ( | ) | const |
Compute and return the Euclidean norm (also called Frobenius norm) 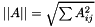 .
.
Definition at line 6900 of file vpMatrix.cpp.
References frobeniusNorm().
Referenced by vpColVector::deg2rad().
| vpMatrix vpMatrix::expm | ( | ) | const |
Compute the exponential matrix of a square matrix.
Definition at line 6495 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, eye(), vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), inverseByLU(), vpArray2D< Type >::resize(), row(), vpArray2D< double >::rowNum, and sum().
Referenced by vpTemplateTrackerWarpHomographySL3::computeCoeff().
| vpMatrix vpMatrix::extract | ( | unsigned int | r, |
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) | const |
Extract a sub matrix from a matrix M.
| r | : row index in matrix M. |
| c | : column index in matrix M. |
| nrows | : Number of rows of the matrix that should be extracted. |
| ncols | : Number of columns of the matrix that should be extracted. |
The following code shows how to use this function:
It produces the following output:
Definition at line 407 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< Type >::resize().
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), solveByQR(), and vpVelocityTwistMatrix::~vpVelocityTwistMatrix().
| void vpMatrix::eye | ( | ) |
Set an m-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 449 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpServo::computeControlLaw(), computeCovarianceMatrixVVS(), vpMbDepthDenseTracker::computeVVS(), vpMbDepthNormalTracker::computeVVS(), vpMbGenericTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpMbTracker::computeVVSPoseEstimation(), expm(), eye(), vpTemplateTrackerWarpHomographySL3::getdW0(), vpTemplateTrackerWarpHomographySL3::getdWdp0(), vpFeatureThetaU::interaction(), vpMeLine::leastSquare(), vpPose::poseFromRectangle(), vpRobotKinova::setCartVelocity(), vpServo::setServo(), vpLinProg::solveLP(), vpMbGenericTracker::track(), vpMbTracker::vpMbTracker(), vpRobotCamera::vpRobotCamera(), vpServo::vpServo(), vpSimulatorCamera::vpSimulatorCamera(), and vpVelocityTwistMatrix::~vpVelocityTwistMatrix().
| void vpMatrix::eye | ( | unsigned int | n | ) |
Set an n-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 432 of file vpMatrix.cpp.
References eye().
| void vpMatrix::eye | ( | unsigned int | m, |
| unsigned int | n | ||
| ) |
Set an m-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 438 of file vpMatrix.cpp.
References eye(), and vpArray2D< double >::resize().
| double vpMatrix::frobeniusNorm | ( | ) | const |
Compute and return the Frobenius norm (also called Euclidean norm) 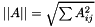 .
.
Definition at line 6704 of file vpMatrix.cpp.
References vpArray2D< double >::data, and vpArray2D< double >::dsize.
Referenced by euclideanNorm(), and vpColVector::extract().
| vpColVector vpMatrix::getCol | ( | unsigned int | j | ) | const |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If j=0, the first column is extracted. |
The following example shows how to use this function:
It produces the following output:
Definition at line 5175 of file vpMatrix.cpp.
References vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpHomography::DLT(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), kernel(), vpPose::poseFromRectangle(), vpServo::secondaryTaskJointLimitAvoidance(), and vpLinProg::simplex().
| vpColVector vpMatrix::getCol | ( | unsigned int | j, |
| unsigned int | i_begin, | ||
| unsigned int | column_size | ||
| ) | const |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If col=0, the first column is extracted. |
| i_begin | : Index of the row that gives the location of the first element of the column vector to extract. |
| column_size | : Size of the column vector to extract. |
The following example shows how to use this function:
It produces the following output:
Definition at line 5126 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
|
inlineinherited |
Return the number of columns of the 2D array.
Definition at line 279 of file vpArray2D.h.
References vpArray2D< Type >::colNum, vpArray2D< Type >::getMaxValue(), and vpArray2D< Type >::getMinValue().
Referenced by cond(), vpRowVector::cppPrint(), cppPrint(), vpRowVector::csvPrint(), csvPrint(), detByLUEigen3(), extract(), vpRotationMatrix::getCol(), vpHomogeneousMatrix::getCol(), getCol(), inducedL2Norm(), inverseByLUEigen3(), inverseByQRLapack(), vpRotationMatrix::isARotationMatrix(), kernel(), vpRowVector::maplePrint(), maplePrint(), vpRowVector::matlabPrint(), matlabPrint(), nullSpace(), vpRowVector::operator*(), vpRowVector::operator+(), vpRowVector::operator+=(), vpRowVector::operator-(), vpRowVector::operator-=(), vpForceTwistMatrix::print(), vpVelocityTwistMatrix::print(), vpRowVector::print(), print(), pseudoInverse(), row(), svdEigen3(), svdLapack(), and svdOpenCV().
| vpColVector vpMatrix::getDiag | ( | ) | const |
Extract a diagonal vector from a matrix.
The following example shows how to use this function:
It produces the following output:
Definition at line 5307 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, diag(), vpColVector::resize(), and vpArray2D< double >::rowNum.
|
inlinestatic |
Return the minimum size of rows and columns required to enable Blas/Lapack usage on matrices and vectors.
To get more info see Tutorial: Basic linear algebra operations.
Definition at line 246 of file vpMatrix.h.
|
inherited |
Return the array max value.
|
inherited |
Return the array min value.
| vpRowVector vpMatrix::getRow | ( | unsigned int | i | ) | const |
Extract a row vector from a matrix.
| i | : Index of the row to extract. If i=0, the first row is extracted. |
The following example shows how to use this function:
It produces the following output:
Definition at line 5215 of file vpMatrix.cpp.
References vpArray2D< double >::colNum.
Referenced by vpLinProg::allClose(), vpLinProg::allLesser(), vpLinProg::solveLP(), and vpQuadProg::solveQPi().
| vpRowVector vpMatrix::getRow | ( | unsigned int | i, |
| unsigned int | j_begin, | ||
| unsigned int | row_size | ||
| ) | const |
Extract a row vector from a matrix.
| i | : Index of the row to extract. If i=0, the first row is extracted. |
| j_begin | : Index of the column that gives the location of the first element of the row vector to extract. |
| row_size | : Size of the row vector to extract. |
The following example shows how to use this function:
It produces the following output:
Definition at line 5259 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, and vpArray2D< double >::rowNum.
|
inlineinherited |
Return the number of rows of the 2D array.
Definition at line 289 of file vpArray2D.h.
References vpArray2D< Type >::rowNum.
Referenced by column(), cond(), vpColVector::cppPrint(), cppPrint(), vpColVector::csvPrint(), csvPrint(), detByLUEigen3(), extract(), vpRotationMatrix::getCol(), vpHomogeneousMatrix::getCol(), getCol(), inducedL2Norm(), inverseByCholeskyLapack(), inverseByLUEigen3(), inverseByQRLapack(), vpRotationMatrix::isARotationMatrix(), kernel(), vpColVector::maplePrint(), maplePrint(), vpColVector::matlabPrint(), matlabPrint(), nullSpace(), vpColVector::operator+(), vpColVector::operator+=(), vpColVector::operator-(), vpColVector::operator-=(), vpForceTwistMatrix::print(), vpVelocityTwistMatrix::print(), vpPoseVector::print(), vpColVector::print(), print(), pseudoInverse(), svdEigen3(), svdLapack(), and svdOpenCV().
Compute the Hadamard product (element wise matrix multiplication).
| m | : Second matrix; |
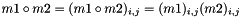
Definition at line 1767 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
Compute the Hadamard product (element wise matrix multiplication).
| m | : Second matrix; |
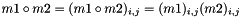
| double vpMatrix::inducedL2Norm | ( | ) | const |
Compute and return the induced L2 norm 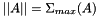 which is equal to the maximum singular value of the matrix.
which is equal to the maximum singular value of the matrix.
Definition at line 6723 of file vpMatrix.cpp.
References vpArray2D< double >::dsize, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::size(), and svd().
| double vpMatrix::infinityNorm | ( | ) | const |
Compute and return the infinity norm 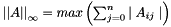 with
with 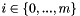 where
where 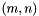 is the matrix size.
is the matrix size.
Definition at line 6764 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by vpLinProg::colReduction(), vpColVector::extract(), and vpLinProg::rowReduction().
| void vpMatrix::init | ( | const vpMatrix & | M, |
| unsigned int | r, | ||
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) |
Initialize the matrix from a part of an input matrix M.
| M | : Input matrix used for initialization. |
| r | : row index in matrix M. |
| c | : column index in matrix M. |
| nrows | : Number of rows of the matrix that should be initialized. |
| ncols | : Number of columns of the matrix that should be initialized. |
The sub-matrix starting from M[r][c] element and ending on M[r+nrows-1][c+ncols-1] element is used to initialize the matrix.
The following code shows how to use this function:
It produces the following output:
Definition at line 346 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
|
inline |
Definition at line 781 of file vpMatrix.h.
Referenced by vpColVector::extract(), vpMatrix(), and vpSubMatrix::vpSubMatrix().
| void vpMatrix::insert | ( | const vpMatrix & | A, |
| unsigned int | r, | ||
| unsigned int | c | ||
| ) |
Insert matrix A at the given position in the current matrix.
| A | : The matrix to insert. |
| r | : The index of the row to begin to insert data. |
| c | : The index of the column to begin to insert data. |
Definition at line 5988 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, and vpArray2D< Type >::size().
Referenced by vpMbEdgeKltTracker::computeVVS(), vpMbDepthDenseTracker::computeVVSInteractionMatrixAndResidu(), vpMbDepthNormalTracker::computeVVSInteractionMatrixAndResidu(), vpMbGenericTracker::computeVVSInteractionMatrixAndResidu(), cond(), conv2(), vpNurbs::curveKnotIns(), vpColVector::extract(), insert(), juxtaposeMatrices(), kernel(), nullSpace(), pseudoInverse(), vpRobotKinova::setCartVelocity(), stack(), vpColVector::stackMatrices(), and vpMbGenericTracker::track().
|
static |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| r | : Index of the row where to add the matrix. |
| c | : Index of the column where to add the matrix. |
Definition at line 5478 of file vpMatrix.cpp.
References insert().
|
static |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| C | : Result matrix. |
| r | : Index of the row where to insert matrix B. |
| c | : Index of the column where to insert matrix B. |
Definition at line 5500 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
| vpMatrix vpMatrix::inverseByCholesky | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition. The matrix must be real symmetric positive defined.
This function calls the first following function that is available:
If none of these 3rd parties is installed we use a Lapack built-in version.
Here an example:
Definition at line 112 of file vpMatrix_cholesky.cpp.
References vpException::fatalError, inverseByCholeskyLapack(), and inverseByCholeskyOpenCV().
| vpMatrix vpMatrix::inverseByCholeskyLapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition with Lapack 3rd party. The matrix must be real symmetric positive defined.
Here an example:
Definition at line 162 of file vpMatrix_cholesky.cpp.
References vpException::badValue, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::fatalError, vpArray2D< Type >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::getRows(), vpMatrixException::matrixError, and vpArray2D< double >::rowNum.
Referenced by inverseByCholesky().
| vpMatrix vpMatrix::inverseByCholeskyOpenCV | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition with OpenCV 3rd party. The matrix must be real symmetric positive defined.
Here an example:
Definition at line 255 of file vpMatrix_cholesky.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByCholesky().
| vpMatrix vpMatrix::inverseByLU | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition.
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default inverseByLULapack() with a Lapack built-in version.
Here an example:
Definition at line 130 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, det(), vpException::fatalError, inverseByLUEigen3(), inverseByLULapack(), inverseByLUOpenCV(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
Referenced by vpTriangle::buildFrom(), expm(), vpKalmanFilter::filtering(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerTriangle::init(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerMIForwardCompositional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTrackerMIForwardAdditional::initHessienDesired(), vpTemplateTrackerMIESM::initHessienDesired(), vpTemplateTrackerMIInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), vpTemplateTrackerSSDForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIInverseCompositional::trackNoPyr(), vpTemplateTrackerWarp::warp(), and vpImageTools::warpImage().
| vpMatrix vpMatrix::inverseByLUEigen3 | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with Eigen3 3rd party.
Here an example:
Definition at line 572 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByLULapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with Lapack 3rd party.
Here an example:
Definition at line 281 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByLUOpenCV | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with OpenCV 3rd party.
Here an example:
Definition at line 483 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByQR | ( | ) | const |
Compute the inverse of a n-by-n matrix using the QR decomposition. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
Here an example:
Definition at line 381 of file vpMatrix_qr.cpp.
References vpException::fatalError, and inverseByQRLapack().
Referenced by vpLinProg::simplex().
| vpMatrix vpMatrix::inverseByQRLapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the QR decomposition with Lapack 3rd party.
Here an example:
Definition at line 152 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::getRows(), vpMatrixException::matrixError, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< Type >::rowNum.
Referenced by inverseByQR().
| vpMatrix vpMatrix::inverseTriangular | ( | bool | upper = true | ) | const |
Compute the inverse of a full-rank n-by-n triangular matrix. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| upper | : if it is an upper triangular matrix |
The function does not check if the matrix is actually upper or lower triangular.
Definition at line 1024 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpMatrixException::rankDeficient, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< Type >::rowNum.
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
Juxtapose to matrices C = [ A B ].
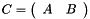
| A | : Left matrix. |
| B | : Right matrix. |
Definition at line 5531 of file vpMatrix.cpp.
Referenced by vpLinProg::colReduction().
Juxtapose to matrices C = [ A B ].
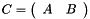
| A | : Left matrix. |
| B | : Right matrix. |
| C | : Juxtaposed matrix C = [ A B ] |
Definition at line 5552 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), and vpArray2D< Type >::resize().
| unsigned int vpMatrix::kernel | ( | vpMatrix & | kerAt, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix  .
.
The null space of a matrix  is defined as
is defined as 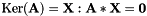 .
.
| kerAt | The matrix that contains the null space (kernel) of  defined by the matrix defined by the matrix 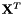 . If matrix . If matrix  is full rank, the dimension of is full rank, the dimension of kerAt is (0, n), otherwise the dimension is (n-r, n). This matrix is thus the transpose of 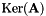 . . |
| svThreshold | Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Definition at line 6265 of file vpMatrix.cpp.
References getCol(), vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::getRows(), insert(), vpArray2D< Type >::resize(), vpColVector::resize(), vpColVector::sumSquare(), and svd().
Compute Kronecker product matrix.
| m | : vpMatrix. |
| out | : If m1.kron(m2) out contains the kronecker product's result :  . . |
Definition at line 1817 of file vpMatrix.cpp.
Referenced by kron().
Compute Kronecker product matrix.
| m | : vpMatrix; |

Definition at line 1856 of file vpMatrix.cpp.
References kron().
Compute Kronecker product matrix.
Definition at line 1787 of file vpMatrix.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
Compute Kronecker product matrix.

Definition at line 1825 of file vpMatrix.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
|
inlinestaticinherited |
Load a matrix from a file.
| filename | : Absolute file name. |
| A | : Array to be loaded |
| binary | : If true the matrix is loaded from a binary file, else from a text file. |
| header | : Header of the file is loaded in this parameter. |
Definition at line 540 of file vpArray2D.h.
References vpException::badValue, and vpArray2D< Type >::resize().
|
inlinestatic |
Load a matrix from a file. This function overloads vpArray2D::load().
| filename | : absolute file name. |
| M | : matrix to be loaded. |
| binary | :If true the matrix is loaded from a binary file, else from a text file. |
| header | : Header of the file is loaded in this parameter |
Definition at line 713 of file vpMatrix.h.
References vpArray2D< Type >::load().
Referenced by vpDot2::defineDots().
|
inlinestatic |
Load a matrix from a YAML-formatted file. This function overloads vpArray2D::loadYAML().
| filename | : absolute file name. |
| M | : matrix to be loaded from the file. |
| header | : Header of the file is loaded in this parameter. |
Definition at line 729 of file vpMatrix.h.
References vpArray2D< Type >::loadYAML().
|
inlinestaticinherited |
Load an array from a YAML-formatted file.
| filename | : absolute file name. |
| A | : array to be loaded from the file. |
| header | : header of the file is loaded in this parameter. |
Definition at line 652 of file vpArray2D.h.
References vpArray2D< Type >::resize().
| std::ostream & vpMatrix::maplePrint | ( | std::ostream & | os | ) | const |
Print using Maple syntax, to copy/paste in Maple later.
The following code
produces this output:
that could be copy/paste in Maple.
Definition at line 5765 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
Referenced by vpColVector::extract().
| std::ostream & vpMatrix::matlabPrint | ( | std::ostream & | os | ) | const |
Print using Matlab syntax, to copy/paste in Matlab later.
The following code
produces this output:
that could be copy/paste in Matlab:
Definition at line 5721 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
Referenced by vpColVector::extract().
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1009 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator*().
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If matrices are not 3-by-3 dimension. |
Definition at line 1065 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If matrices are not 4-by-4 dimension. |
Definition at line 1102 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1159 of file vpMatrix.cpp.
References multMatrixVector().
|
static |
Operation w = A * v (v and w are vectors).
A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 959 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by mult2Matrices(), and operator*().
Operation C = -A.
The result is placed in the second parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 1540 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator-().
| unsigned int vpMatrix::nullSpace | ( | vpMatrix & | kerA, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix  .
.
The null space of a matrix  is defined as
is defined as 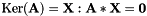 .
.
| kerA | The matrix that contains the null space (kernel) of  . If matrix . If matrix  is full rank, the dimension of is full rank, the dimension of kerA is (n, 0), otherwise its dimension is (n, n-r). |
| svThreshold | Threshold used to test the singular values. The dimension of kerA corresponds to the number of singular values lower than this threshold |
 .
. Definition at line 6336 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpArray2D< Type >::resize(), vpColVector::resize(), and svd().
Referenced by vpMeEllipse::leastSquare(), and vpMeEllipse::leastSquareRobust().
| unsigned int vpMatrix::nullSpace | ( | vpMatrix & | kerA, |
| int | dim | ||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix  .
.
The null space of a matrix  is defined as
is defined as 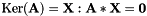 .
.
| kerA | The matrix that contains the null space (kernel) of  . If matrix . If matrix  is full rank, the dimension of is full rank, the dimension of kerA is (n, 0), otherwise its dimension is (n, n-r). |
| dim | the dimension of the null space when it is known a priori |
 , by using 1e-6 as threshold for the sigular values.
, by using 1e-6 as threshold for the sigular values. Definition at line 6401 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpArray2D< Type >::resize(), vpColVector::resize(), and svd().
Not equal to comparison operator of a 2D array.
Operation C = A * B (A is unchanged).
Definition at line 1168 of file vpMatrix.cpp.
References mult2Matrices().
Referenced by vpColVector::operator[](), vpColVector::stackMatrices(), and vpVelocityTwistMatrix::~vpVelocityTwistMatrix().
| vpMatrix vpMatrix::operator* | ( | const vpRotationMatrix & | R | ) | const |
Operator that allow to multiply a matrix by a rotation matrix. The matrix should be of dimension m-by-3.
Definition at line 1181 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | const vpHomogeneousMatrix & | M | ) | const |
Operator that allow to multiply a matrix by a homogeneous matrix. The matrix should be of dimension m-by-4.
Definition at line 1210 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | const vpVelocityTwistMatrix & | V | ) | const |
Operator that allow to multiply a matrix by a velocity twist matrix. The matrix should be of dimension m-by-6.
Definition at line 1239 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
| vpMatrix vpMatrix::operator* | ( | const vpForceTwistMatrix & | V | ) | const |
Operator that allow to multiply a matrix by a force/torque twist matrix. The matrix should be of dimension m-by-6.
Definition at line 1278 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
| vpTranslationVector vpMatrix::operator* | ( | const vpTranslationVector & | tv | ) | const |
Operator that allows to multiply a matrix by a translation vector. The matrix should be of dimension (3x3)
Definition at line 919 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpColVector vpMatrix::operator* | ( | const vpColVector & | v | ) | const |
Operation w = A * v (matrix A is unchanged, v and w are column vectors).
Definition at line 944 of file vpMatrix.cpp.
References multMatrixVector().
| vpMatrix vpMatrix::operator* | ( | double | x | ) | const |
Operator that allows to multiply all the elements of a matrix by a scalar.
Definition at line 1612 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator*= | ( | double | x | ) |
Multiply all the element of the matrix by x : Aij = Aij * x.
Operator that allows to multiply all the elements of a matrix by a scalar.
Definition at line 1675 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by vpColVector::operator[]().
Operation C = A + B (A is unchanged).
Definition at line 1410 of file vpMatrix.cpp.
References add2Matrices().
Referenced by vpColVector::operator[]().
Operation A = A + B.
Definition at line 1499 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, vpArray2D< Type >::rowPtrs, and vpArray2D< double >::rowPtrs.
Referenced by vpColVector::operator[]().
| vpMatrix & vpMatrix::operator+= | ( | double | x | ) |
Add x to all the element of the matrix : Aij = Aij + x.
Definition at line 1652 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator, | ( | double | val | ) |
Definition at line 805 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
Referenced by vpColVector::operator[]().
Operation C = A - B (A is unchanged).
Definition at line 1490 of file vpMatrix.cpp.
References sub2Matrices().
| vpMatrix vpMatrix::operator- | ( | void | ) | const |
Operation C = -A (A is unchanged).
Definition at line 1558 of file vpMatrix.cpp.
References negateMatrix().
Referenced by vpColVector::operator[]().
Operation A = A - B.
Definition at line 1516 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, vpArray2D< Type >::rowPtrs, and vpArray2D< double >::rowPtrs.
Referenced by vpColVector::operator[]().
| vpMatrix & vpMatrix::operator-= | ( | double | x | ) |
Substract x to all the element of the matrix : Aij = Aij - x.
Definition at line 1662 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator/ | ( | double | x | ) | const |
Cij = Aij / x (A is unchanged)
Definition at line 1629 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::divideByZeroError, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by vpColVector::operator[]().
| vpMatrix & vpMatrix::operator/= | ( | double | x | ) |
Divide all the element of the matrix by x : Aij = Aij / x.
Definition at line 1689 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::divideByZeroError, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by vpColVector::operator[]().
| vpMatrix & vpMatrix::operator<< | ( | double * | x | ) |
Assigment from an array of double. This method has to be used carefully since the array allocated behind x pointer should have the same dimension than the matrix.
Definition at line 788 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator<< | ( | double | val | ) |
Definition at line 798 of file vpMatrix.cpp.
References vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
Copy operator that allows to convert on of the following container that inherit from vpArray2D such as vpMatrix, vpRotationMatrix, vpHomogeneousMatrix, vpPoseVector, vpColVector, vpRowVector... into a vpMatrix.
| A | : 2D array to be copied. |
The following example shows how to create a matrix from an homogeneous matrix:
Definition at line 654 of file vpMatrix.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
Definition at line 666 of file vpMatrix.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
Definition at line 677 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< double >::dsize, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator= | ( | const std::initializer_list< double > & | list | ) |
Set matrix elements from a list of values.
| list | : List of double. Matrix size (number of columns multiplied by number of columns) should match the number of elements. |
Definition at line 723 of file vpMatrix.cpp.
References vpArray2D< double >::data, vpArray2D< double >::dsize, and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const std::initializer_list< std::initializer_list< double > > & | lists | ) |
Set matrix elements from a list of values.
| lists | : List of double. |
Definition at line 757 of file vpMatrix.cpp.
References vpArray2D< double >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator= | ( | double | x | ) |
Set all the element of the matrix A to x.
Definition at line 777 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, and vpArray2D< double >::rowNum.
Equal to comparison operator of a 2D array.
|
inlineinherited |
Set element 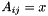 using A[i][j] = x.
using A[i][j] = x.
Definition at line 484 of file vpArray2D.h.
|
inlineinherited |
Get element 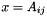 using x = A[i][j].
using x = A[i][j].
Definition at line 486 of file vpArray2D.h.
| int vpMatrix::print | ( | std::ostream & | s, |
| unsigned int | length, | ||
| const std::string & | intro = "" |
||
| ) | const |
Pretty print a matrix. The data are tabulated. The common widths before and after the decimal point are set with respect to the parameter maxlen.
| s | Stream used for the printing. |
| length | The suggested width of each matrix element. The actual width grows in order to accomodate the whole integral part, and shrinks if the whole extent is not needed for all the numbers. |
| intro | The introduction which is printed before the matrix. Can be set to zero (or omitted), in which case the introduction is not printed. |
Definition at line 5598 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpMath::maximum().
Referenced by vpServo::computeControlLaw(), vpColVector::operator[](), and vpVelocityTwistMatrix::~vpVelocityTwistMatrix().
|
inline |
Definition at line 597 of file vpMatrix.h.
References vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
| vpMatrix vpMatrix::pseudoInverse | ( | double | svThreshold = 1e-6 | ) | const |
Compute and return the Moore-Penros pseudo inverse 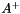 of a m-by-n matrix
of a m-by-n matrix  .
.
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2241 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
Referenced by vpSimulatorAfma6::computeArticularVelocity(), vpSimulatorViper850::computeArticularVelocity(), vpServo::computeControlLaw(), computeCovarianceMatrix(), computeCovarianceMatrixVVS(), vpPoseFeatures::computePose(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpMbTracker::computeVVSPoseEstimation(), vpQuadProg::fromCanonicalCost(), vpNurbs::globalCurveApprox(), vpNurbs::globalCurveInterp(), vpHomography::inverse(), vpMeLine::leastSquare(), vpRotationMatrix::mean(), vpHomogeneousMatrix::mean(), vpPose::poseDementhonNonPlan(), vpPose::poseDementhonPlan(), vpPose::poseFromRectangle(), vpPose::poseVirtualVS(), pseudoInverse(), vpHomography::robust(), solveBySVD(), and vpQuadProg::solveQPi().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Compute the Moore-Penros pseudo inverse  of a m-by-n matrix
of a m-by-n matrix  and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse 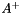 . . |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2099 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
Compute the Moore-Penros pseudo inverse 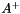 of a m-by-n matrix
of a m-by-n matrix  along with singular values and return the rank of the matrix.
along with singular values and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse  . . |
| sv | Vector corresponding to matrix 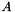 singular values. The size of this vector is equal to min(m, n). singular values. The size of this vector is equal to min(m, n). |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4509 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse 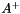 of a m-by-n matrix
of a m-by-n matrix  along with singular values,
along with singular values, 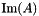 and
and 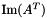 and return the rank of the matrix.
and return the rank of the matrix.
See pseudoInverse(vpMatrix &, vpColVector &, double, vpMatrix &, vpMatrix &, vpMatrix &) const for a complete description of this function.
| Ap | : The Moore-Penros pseudo inverse 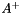 . . |
| sv | Vector corresponding to matrix 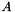 singular values. The size of this vector is equal to min(m, n). singular values. The size of this vector is equal to min(m, n). |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
| imA | 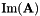 that is a m-by-r matrix. that is a m-by-r matrix. |
| imAt | 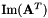 that is n-by-r matrix. that is n-by-r matrix. |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4682 of file vpMatrix.cpp.
References pseudoInverse().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse 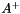 of a m-by-n matrix
of a m-by-n matrix  along with singular values,
along with singular values, 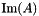 ,
, 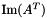 and
and 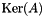 and return the rank of the matrix.
and return the rank of the matrix.
Using singular value decomposition, we have:
![\[ {\bf A}_{m\times n} = {\bf U}_{m\times m} \; {\bf S}_{m\times n} \; {\bf V^\top}_{n\times n} \]](form_448.png)
![\[ {\bf A}_{m\times n} = \left[\begin{array}{ccc}\mbox{Im} ({\bf A}) & | & \mbox{Ker} ({\bf A}^\top) \end{array} \right] {\bf S}_{m\times n} \left[ \begin{array}{c} \left[\mbox{Im} ({\bf A}^\top)\right]^\top \\ \\ \hline \\ \left[\mbox{Ker}({\bf A})\right]^\top \end{array}\right] \]](form_449.png)
where the diagonal of 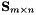 corresponds to the matrix
corresponds to the matrix 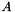 singular values.
singular values.
This equation could be reformulated in a minimal way:
![\[ {\bf A}_{m\times n} = \mbox{Im} ({\bf A}) \; {\bf S}_{r\times n} \left[ \begin{array}{c} \left[\mbox{Im} ({\bf A}^\top)\right]^\top \\ \\ \hline \\ \left[\mbox{Ker}({\bf A})\right]^\top \end{array}\right] \]](form_451.png)
where the diagonal of 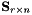 corresponds to the matrix
corresponds to the matrix 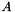 first r singular values.
first r singular values.
The null space of a matrix  is defined as
is defined as 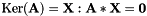 .
.
| Ap | The Moore-Penros pseudo inverse 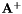 . . |
| sv | Vector corresponding to matrix 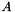 singular values. The size of this vector is equal to min(m, n). singular values. The size of this vector is equal to min(m, n). |
| svThreshold | Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
| imA | 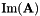 that is a m-by-r matrix. that is a m-by-r matrix. |
| imAt | 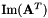 that is n-by-r matrix. that is n-by-r matrix. |
| kerAt | The matrix that contains the null space (kernel) of  defined by the matrix defined by the matrix 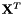 . If matrix . If matrix  is full rank, the dimension of is full rank, the dimension of kerAt is (0, n), otherwise the dimension is (n-r, n). This matrix is thus the transpose of 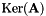 . . |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4906 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| vpMatrix vpMatrix::pseudoInverse | ( | int | rank_in | ) | const |
Compute and return the Moore-Penros pseudo inverse  of a m-by-n matrix
of a m-by-n matrix  .
.
| [in] | rank_in | : Known rank of the matrix. |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2306 of file vpMatrix.cpp.
References vpArray2D< Type >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), pseudoInverseEigen3(), pseudoInverseLapack(), pseudoInverseOpenCV(), vpArray2D< Type >::resize(), vpColVector::resize(), vpArray2D< Type >::size(), svdEigen3(), svdLapack(), and svdOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
Compute the Moore-Penros pseudo inverse 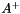 of a m-by-n matrix
of a m-by-n matrix  and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse 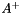 . . | |
| [in] | rank_in | : Known rank of the matrix. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2175 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
Compute the Moore-Penros pseudo inverse  of a m-by-n matrix
of a m-by-n matrix  along with singular values and return the rank of the matrix.
along with singular values and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse 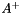 . . | |
| sv | Vector corresponding to matrix 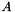 singular values. The size of this vector is equal to min(m, n). singular values. The size of this vector is equal to min(m, n). | |
| [in] | rank_in | : Known rank of the matrix. |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4592 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse 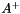 of a m-by-n matrix
of a m-by-n matrix  along with singular values,
along with singular values,  and
and 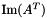 and return the rank of the matrix.
and return the rank of the matrix.
See pseudoInverse(vpMatrix &, vpColVector &, double, vpMatrix &, vpMatrix &, vpMatrix &) const for a complete description of this function.
| Ap | : The Moore-Penros pseudo inverse 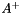 . . | |
| sv | Vector corresponding to matrix 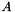 singular values. The size of this vector is equal to min(m, n). singular values. The size of this vector is equal to min(m, n). | |
| [in] | rank_in | : Known rank of the matrix. |
| imA | 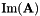 that is a m-by-r matrix. that is a m-by-r matrix. | |
| imAt | 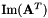 that is n-by-r matrix. that is n-by-r matrix. |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4766 of file vpMatrix.cpp.
References pseudoInverse().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse 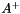 of a m-by-n matrix
of a m-by-n matrix  along with singular values,
along with singular values, 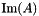 ,
, 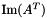 and
and 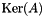 and return the rank of the matrix.
and return the rank of the matrix.
Using singular value decomposition, we have:
![\[ {\bf A}_{m\times n} = {\bf U}_{m\times m} \; {\bf S}_{m\times n} \; {\bf V^\top}_{n\times n} \]](form_448.png)
![\[ {\bf A}_{m\times n} = \left[\begin{array}{ccc}\mbox{Im} ({\bf A}) & | & \mbox{Ker} ({\bf A}^\top) \end{array} \right] {\bf S}_{m\times n} \left[ \begin{array}{c} \left[\mbox{Im} ({\bf A}^\top)\right]^\top \\ \\ \hline \\ \left[\mbox{Ker}({\bf A})\right]^\top \end{array}\right] \]](form_449.png)
where the diagonal of 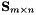 corresponds to the matrix
corresponds to the matrix 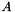 singular values.
singular values.
This equation could be reformulated in a minimal way:
![\[ {\bf A}_{m\times n} = \mbox{Im} ({\bf A}) \; {\bf S}_{r\times n} \left[ \begin{array}{c} \left[\mbox{Im} ({\bf A}^\top)\right]^\top \\ \\ \hline \\ \left[\mbox{Ker}({\bf A})\right]^\top \end{array}\right] \]](form_451.png)
where the diagonal of 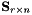 corresponds to the matrix
corresponds to the matrix 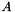 first r singular values.
first r singular values.
The null space of a matrix  is defined as
is defined as 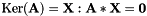 .
.
| Ap | The Moore-Penros pseudo inverse 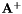 . . | |
| sv | Vector corresponding to matrix 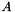 singular values. The size of this vector is equal to min(m, n). singular values. The size of this vector is equal to min(m, n). | |
| [in] | rank_in | : Known rank of the matrix. |
| imA | 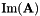 that is a m-by-r matrix. that is a m-by-r matrix. | |
| imAt | 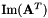 that is n-by-r matrix. that is n-by-r matrix. | |
| kerAt | The matrix that contains the null space (kernel) of  defined by the matrix defined by the matrix 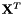 . If matrix . If matrix  is full rank, the dimension of is full rank, the dimension of kerAt is (0, n), otherwise the dimension is (n-r, n). This matrix is thus the transpose of  . . |
 .
.Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 5065 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| vpMatrix vpMatrix::pseudoInverseEigen3 | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseEigen3 | ( | int | rank_in | ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseLapack | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseLapack | ( | int | rank_in | ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseOpenCV | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseOpenCV | ( | int | rank_in | ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::qr | ( | vpMatrix & | Q, |
| vpMatrix & | R, | ||
| bool | full = false, |
||
| bool | squareR = false, |
||
| double | tol = 1e-6 |
||
| ) | const |
Compute the QR decomposition of a (m x n) matrix of rank r. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| Q | : orthogonal matrix (will be modified). |
| R | : upper-triangular matrix (will be modified). |
| full | : whether or not we want full decomposition. |
| squareR | : will return only the square (min(m,n) x min(m,n)) part of R. |
| tol | : tolerance to test the rank of R. |
If full is false (default) then Q is (m x min(n,m)) and R is (min(n,m) x n). We then have this = QR.
If full is true and m > n then Q is (m x m) and R is (n x n). In this case this = Q (R, 0)^T
If squareR is true and n > m then R is (m x m). If r = m then R is invertible.
Here an example:
Definition at line 444 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::fatalError, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction().
| unsigned int vpMatrix::qrPivot | ( | vpMatrix & | Q, |
| vpMatrix & | R, | ||
| vpMatrix & | P, | ||
| bool | full = false, |
||
| bool | squareR = false, |
||
| double | tol = 1e-6 |
||
| ) | const |
Compute the QR pivot decomposition of a (m x n) matrix of rank r. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| Q | : orthogonal matrix (will be modified). |
| R | : upper-triangular matrix (will be modified). |
| P | : the (n x n) permutation matrix. |
| full | : whether or not we want full decomposition. |
| squareR | : will return only the (r x r) part of R and the (r x n) part of P. |
| tol | : tolerance to test the rank of R. |
If full is false (default) then Q is (m x min(n,m)) and R is (min(n,m) x n). We then have this.P = Q.R.
If full is true and m > n then Q is (m x m) and R is (n x n). In this case this.P = Q (R, 0)^T
If squareR is true then R is (r x r) invertible.
Here an example:
Definition at line 737 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::fatalError, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< Type >::rowNum.
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
|
inlineinherited |
Definition at line 379 of file vpArray2D.h.
References vpException::dimensionError, vpArray2D< Type >::dsize, vpArray2D< Type >::operator!=(), vpArray2D< Type >::operator==(), vpArray2D< Type >::resize(), and vpArray2D< Type >::rowPtrs.
|
inlineinherited |
Set the size of the array and initialize all the values to zero.
| nrows | : number of rows. |
| ncols | : number of column. |
| flagNullify | : if true, then the array is re-initialized to 0 after resize. If false, the initial values from the common part of the array (common part between old and new version of the array) are kept. Default value is true. |
| recopy_ | : if true, will perform an explicit recopy of the old data. |
Definition at line 304 of file vpArray2D.h.
References vpArray2D< Type >::colNum, vpArray2D< Type >::dsize, vpException::memoryAllocationError, vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by diag(), eye(), init(), operator,(), operator<<(), operator=(), stack(), and svdOpenCV().
| vpRowVector vpMatrix::row | ( | unsigned int | i | ) |
should be replaced with:
| i | : Index of the row to extract noting that row index start at 1 to get the first row. |
Definition at line 6937 of file vpMatrix.cpp.
References vpArray2D< double >::getCols().
Referenced by expm().
|
inlinestaticinherited |
Save a matrix to a file.
| filename | : Absolute file name. |
| A | : Array to be saved. |
| binary | : If true the matrix is saved in a binary file, else a text file. |
| header | : Optional line that will be saved at the beginning of the file. |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 737 of file vpArray2D.h.
References vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
|
inlinestatic |
Save a matrix to a file. This function overloads vpArray2D::load().
| filename | : absolute file name. |
| M | : matrix to be saved. |
| binary | : If true the matrix is save in a binary file, else a text file. |
| header | : optional line that will be saved at the beginning of the file. |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 748 of file vpMatrix.h.
References vpArray2D< Type >::save().
Referenced by vpDot2::defineDots().
|
inlinestatic |
Save a matrix in a YAML-formatted file. This function overloads vpArray2D::saveYAML().
| filename | : absolute file name. |
| M | : matrix to be saved in the file. |
| header | : optional lines that will be saved at the beginning of the file. Should be YAML-formatted and will adapt to the indentation if any. |
Definition at line 766 of file vpMatrix.h.
References vpArray2D< Type >::saveYAML().
|
inlinestaticinherited |
Save an array in a YAML-formatted file.
| filename | : absolute file name. |
| A | : array to be saved in the file. |
| header | : optional lines that will be saved at the beginning of the file. Should be YAML-formatted and will adapt to the indentation if any. |
Here is an example of outputs.
Content of matrix.yml:
Content of matrixIndent.yml:
Definition at line 830 of file vpArray2D.h.
References vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
| void vpMatrix::setIdentity | ( | const double & | val = 1.0 | ) |
Set the matrix diagonal elements to val. More generally set M[i][i] = val.
Definition at line 6978 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by vpVelocityTwistMatrix::init(), vpColVector::rows(), and vpServo::secondaryTask().
|
inlinestatic |
Modify default size used to determine if Blas/Lapack basic linear algebra operations are enabled.
To get more info see Tutorial: Basic linear algebra operations.
| min_size | : Minimum size of rows and columns required for a matrix or a vector to use Blas/Lapack third parties like MKL, OpenBLAS, Netlib or Atlas. When matrix or vector size is lower or equal to this parameter, Blas/Lapack is not used. In that case we prefer use naive code that runs faster for small matrices. |
Definition at line 262 of file vpMatrix.h.
References vpArray2D< Type >::hadamard(), operator*(), vpArray2D< Type >::operator<<, and vpArray2D< Type >::operator=().
|
inlineinherited |
Return the number of elements of the 2D array.
Definition at line 291 of file vpArray2D.h.
References vpArray2D< Type >::rowNum.
Referenced by vpRowVector::insert(), vpColVector::insert(), vpColVector::operator*(), vpRotationVector::operator,(), vpTranslationVector::operator,(), vpRotationMatrix::operator,(), vpHomogeneousMatrix::operator,(), vpQuaternionVector::operator=(), vpTranslationVector::operator=(), vpRxyzVector::operator=(), vpRzyzVector::operator=(), vpRzyxVector::operator=(), vpThetaUVector::operator=(), stack(), vpRotationVector::toStdVector(), vpRowVector::toStdVector(), and vpColVector::toStdVector().
| void vpMatrix::solveByQR | ( | const vpColVector & | b, |
| vpColVector & | x | ||
| ) | const |
Solve a linear system Ax = b using QR Decomposition.
Non destructive wrt. A and b.
| b | : Vector b |
| x | : Vector x |
Here an example:
Definition at line 1170 of file vpMatrix_qr.cpp.
References vpArray2D< double >::colNum, extract(), inverseTriangular(), qrPivot(), and t().
Referenced by solveByQR(), and vpQuadProg::solveSVDorQR().
| vpColVector vpMatrix::solveByQR | ( | const vpColVector & | b | ) | const |
Solve a linear system Ax = b using QR Decomposition.
Non destructive wrt. A and B.
| b | : Vector b |
Here an example:
Definition at line 1222 of file vpMatrix_qr.cpp.
References vpArray2D< double >::colNum, and solveByQR().
| void vpMatrix::solveBySVD | ( | const vpColVector & | b, |
| vpColVector & | x | ||
| ) | const |
Solve a linear system 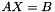 using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| b | : Vector 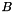 . . |
| x | : Vector 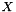 . . |
Here an example:
Definition at line 1908 of file vpMatrix.cpp.
References pseudoInverse().
Referenced by vpQuadProg::solveByProjection(), solveBySVD(), vpQuadProg::solveQPe(), and vpQuadProg::solveSVDorQR().
| vpColVector vpMatrix::solveBySVD | ( | const vpColVector & | B | ) | const |
Solve a linear system 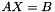 using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| B | : Vector 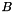 . . |
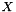 .
.Here an example:
Definition at line 1959 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and solveBySVD().
| void vpMatrix::stack | ( | const vpMatrix & | A | ) |
Stack A at the end of the current matrix, or copy if the matrix has no dimensions : this = [ this A ]^T.
Definition at line 5879 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), vpArray2D< double >::resize(), and vpArray2D< double >::rowNum.
Referenced by vpPoseFeatures::addFeatureSegment(), vpColVector::cross(), vpFeatureVanishingPoint::interaction(), vpFeatureEllipse::interaction(), vpFeatureSegment::interaction(), vpGenericFeature::interaction(), vpFeaturePoint::interaction(), vpFeatureMoment::interaction(), vpFeatureLine::interaction(), vpFeaturePoint3D::interaction(), vpFeatureThetaU::interaction(), vpFeaturePointPolar::interaction(), vpFeatureTranslation::interaction(), vpColVector::resize(), vpLinProg::rowReduction(), stack(), vpColVector::stackMatrices(), and stackMatrices().
| void vpMatrix::stack | ( | const vpRowVector & | r | ) |
Stack row vector r at the end of the current matrix, or copy if the matrix has no dimensions: this = [ this r ]^T.
Here an example for a robot velocity log :
Definition at line 5910 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< double >::resize(), vpArray2D< double >::rowNum, vpArray2D< double >::size(), and vpArray2D< Type >::size().
| void vpMatrix::stack | ( | const vpColVector & | c | ) |
Stack column vector c at the right of the current matrix, or copy if the matrix has no dimensions: this = [ this c ].
Here an example for a robot velocity log matrix:
Here the log matrix has size 6 rows by 100 columns.
Definition at line 5950 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, vpArray2D< Type >::getRows(), vpArray2D< double >::resize(), vpArray2D< double >::rowNum, vpArray2D< double >::rowPtrs, and vpArray2D< Type >::size().
Stack matrix B to the end of matrix A and return the resulting matrix [ A B ]^T
| A | : Upper matrix. |
| B | : Lower matrix. |
Definition at line 5333 of file vpMatrix.cpp.
References stack().
|
static |
Stack row vector r to matrix A and return the resulting matrix [ A r ]^T
| A | : Upper matrix. |
| r | : Lower row vector. |
Definition at line 5397 of file vpMatrix.cpp.
References stack().
|
static |
Stack column vector c to matrix A and return the resulting matrix [ A c ]
| A | : Left matrix. |
| c | : Right column vector. |
Definition at line 5436 of file vpMatrix.cpp.
References stack().
Stack matrix B to the end of matrix A and return the resulting matrix in C.
| A | : Upper matrix. |
| B | : Lower matrix. |
| C | : Stacked matrix C = [ A B ]^T |
Definition at line 5353 of file vpMatrix.cpp.
References vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< Type >::size().
|
static |
Stack row vector r to the end of matrix A and return the resulting matrix in C.
| A | : Upper matrix. |
| r | : Lower row vector. |
| C | : Stacked matrix C = [ A r ]^T |
Definition at line 5416 of file vpMatrix.cpp.
References vpArray2D< Type >::data, and stack().
|
static |
Stack column vector c to the end of matrix A and return the resulting matrix in C.
| A | : Left matrix. |
| c | : Right column vector. |
| C | : Stacked matrix C = [ A c ] |
Definition at line 5455 of file vpMatrix.cpp.
References vpArray2D< Type >::data, and stack().
| void vpMatrix::stackColumns | ( | vpColVector & | out | ) |
Stacks columns of a matrix in a vector.
| out | : a vpColVector. |
Definition at line 1715 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpColVector::resize(), vpArray2D< Type >::rowNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpColVector vpMatrix::stackColumns | ( | ) |
Stacks columns of a matrix in a vector.
Definition at line 1732 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
|
inline |
Definition at line 786 of file vpMatrix.h.
|
inlinestatic |
Definition at line 791 of file vpMatrix.h.
|
inlinestatic |
Definition at line 796 of file vpMatrix.h.
References vpException::fatalError, and operator*().
|
static |
Definition at line 6915 of file vpMatrix.cpp.
References stack().
|
static |
Definition at line 6917 of file vpMatrix.cpp.
References stack().
|
static |
Definition at line 6905 of file vpMatrix.cpp.
References vpColVector::stack().
|
static |
Definition at line 6910 of file vpMatrix.cpp.
References vpColVector::stack().
| void vpMatrix::stackRows | ( | vpRowVector & | out | ) |
Stacks rows of a matrix in a vector
| out | : a vpRowVector. |
Definition at line 1743 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpRowVector::resize(), and vpArray2D< double >::rowNum.
| vpRowVector vpMatrix::stackRows | ( | ) |
Stacks rows of a matrix in a vector.
Definition at line 1754 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Operation C = A - B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If A and B matrices have not the same size. |
Definition at line 1465 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator-().
|
static |
Operation C = A - B on column vectors.
The result is placed in the third parameter C and not returned. A new vector won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If A and B vectors have not the same size. |
Definition at line 1432 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
| double vpMatrix::sum | ( | ) | const |
Return the sum of all the 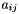 elements of the matrix.
elements of the matrix.
Definition at line 1565 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by expm(), and vpColVector::resize().
| double vpMatrix::sumSquare | ( | ) | const |
Return the sum square of all the 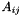 elements of the matrix
elements of the matrix 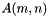 .
.
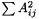 .
. Definition at line 6785 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by vpColVector::resize().
| void vpMatrix::svd | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Matrix singular value decomposition (SVD).
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default svdLapack() with a Lapack built-in version.
Given matrix  , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![\[ M = U \Sigma V^{\top} \]](form_434.png)
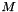 to decompose. You should make a COPY of that matrix if needed.
to decompose. You should make a COPY of that matrix if needed.| w | : Vector of singular values: 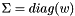 . . |
| V | : Matrix 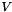 . . |
 .
.Here an example of SVD decomposition of a non square Matrix M.
Definition at line 2030 of file vpMatrix.cpp.
References vpException::fatalError, svdEigen3(), svdLapack(), and svdOpenCV().
Referenced by vpHomography::computeDisplacement(), cond(), vpHomography::DLT(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), inducedL2Norm(), kernel(), nullSpace(), and svdEigen3().
| void vpMatrix::svdEigen3 | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using Eigen3 3rd party.
Given matrix 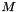 , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![\[ M = U \Sigma V^{\top} \]](form_434.png)
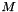 to decompose. You should make a COPY of that matrix if needed.
to decompose. You should make a COPY of that matrix if needed.| w | : Vector of singular values: 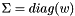 . . |
| V | : Matrix  . . |
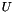 .
.Here an example of SVD decomposition of a non square Matrix M.
Definition at line 411 of file vpMatrix_svd.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::getCols(), vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::getRows(), vpArray2D< Type >::resize(), vpColVector::resize(), vpArray2D< Type >::size(), and svd().
Referenced by pseudoInverse(), and svd().
| void vpMatrix::svdLapack | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using Lapack 3rd party.
Given matrix 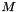 , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![\[ M = U \Sigma V^{\top} \]](form_434.png)
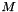 to decompose. You should make a COPY of that matrix if needed.
to decompose. You should make a COPY of that matrix if needed.| w | : Vector of singular values:  . . |
| V | : Matrix 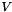 . . |
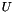 .
.Here an example of SVD decomposition of a non square Matrix M.
Definition at line 240 of file vpMatrix_svd.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::resize(), vpColVector::resize(), vpArray2D< double >::rowNum, and transpose().
Referenced by pseudoInverse(), and svd().
| void vpMatrix::svdOpenCV | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using OpenCV 3rd party.
Given matrix 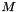 , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![\[ M = U \Sigma V^{\top} \]](form_434.png)
 to decompose. You should make a COPY of that matrix if needed.
to decompose. You should make a COPY of that matrix if needed.| w | : Vector of singular values: 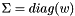 . . |
| V | : Matrix 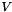 . . |
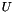 .
.Here an example of SVD decomposition of a non square Matrix M.
Definition at line 153 of file vpMatrix_svd.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::resize(), vpColVector::resize(), and transpose().
Referenced by pseudoInverse(), and svd().
| vpMatrix vpMatrix::t | ( | ) | const |
Compute and return the transpose of the matrix.
Definition at line 464 of file vpMatrix.cpp.
References transpose().
Referenced by vpLinProg::colReduction(), vpServo::computeControlLaw(), computeCovarianceMatrix(), vpTemplateTracker::computeOptimalBrentGain(), eigenValues(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), vpKalmanFilter::filtering(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpQuadProg::fromCanonicalCost(), vpImageFilter::getSobelKernelX(), vpRotationMatrix::mean(), vpHomogeneousMatrix::mean(), vpKalmanFilter::prediction(), vpColVector::resize(), vpLinProg::simplex(), solveByQR(), vpColVector::vpColVector(), vpTemplateTrackerWarp::warp(), and vpVelocityTwistMatrix::~vpVelocityTwistMatrix().
| vpMatrix vpMatrix::transpose | ( | ) | const |
Compute and return the transpose of the matrix.
Definition at line 474 of file vpMatrix.cpp.
Referenced by vpLinProg::colReduction(), vpQuadProg::fromCanonicalCost(), vpColVector::resize(), vpLinProg::rowReduction(), vpLinProg::solveLP(), vpQuadProg::solveQPi(), svdLapack(), svdOpenCV(), and t().
| void vpMatrix::transpose | ( | vpMatrix & | At | ) | const |
Compute At the transpose of the matrix.
| At | (output) : Resulting transpose matrix. |
Definition at line 486 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
Allow to multiply a scalar by a matrix.
Definition at line 1589 of file vpMatrix.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
|
related |
Enumeration of the operations applied on matrices in vpGEMM() function.
Operations are :
|
protectedinherited |
Number of columns in the array.
Definition at line 137 of file vpArray2D.h.
Referenced by AAt(), AtA(), vpColVector::clear(), detByLU(), detByLUEigen3(), detByLULapack(), detByLUOpenCV(), diag(), eigenValues(), expm(), eye(), getDiag(), getRow(), vpColVector::hadamard(), hadamard(), infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpRowVector::insert(), insert(), inverseByCholeskyLapack(), inverseByCholeskyOpenCV(), inverseByLU(), inverseByLUEigen3(), inverseByLULapack(), inverseByLUOpenCV(), inverseByQRLapack(), inverseTriangular(), vpRotationMatrix::operator*(), vpRowVector::operator*(), operator*(), vpRotationMatrix::operator*=(), vpRowVector::operator*=(), operator*=(), vpRowVector::operator+(), vpRowVector::operator+=(), operator+=(), vpRowVector::operator,(), operator,(), vpRowVector::operator-(), vpRowVector::operator-=(), operator-=(), vpRowVector::operator/(), operator/(), vpRowVector::operator/=(), operator/=(), vpColVector::operator<<(), operator<<(), vpSubRowVector::operator=(), vpSubMatrix::operator=(), vpRowVector::operator=(), vpColVector::operator=(), operator=(), vpRowVector::operator==(), vpColVector::operator==(), qr(), qrPivot(), vpRowVector::reshape(), setIdentity(), solveByQR(), solveBySVD(), vpRowVector::stack(), stack(), stackColumns(), stackRows(), vpRowVector::sum(), sum(), vpRowVector::sumSquare(), sumSquare(), svdLapack(), vpRowVector::t(), transpose(), vpColVector::vpColVector(), vpMatrix(), and vpRowVector::vpRowVector().
|
inherited |
Address of the first element of the data array.
Definition at line 145 of file vpArray2D.h.
Referenced by AAt(), AtA(), vpQuaternionVector::buildFrom(), vpHomogeneousMatrix::buildFrom(), vpThetaUVector::buildFrom(), vpRzyzVector::buildFrom(), vpRxyzVector::buildFrom(), vpRzyxVector::buildFrom(), vpSubColVector::checkParentStatus(), vpSubRowVector::checkParentStatus(), vpSubMatrix::checkParentStatus(), vpColVector::clear(), vpHomogeneousMatrix::convert(), detByLUEigen3(), detByLUOpenCV(), expm(), vpThetaUVector::extract(), frobeniusNorm(), getRow(), vpThetaUVector::getTheta(), vpThetaUVector::getU(), vpColVector::hadamard(), hadamard(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpColVector::insert(), insert(), inverseByCholeskyOpenCV(), inverseByLUEigen3(), inverseByLUOpenCV(), vpTranslationVector::operator*(), vpRowVector::operator*(), vpHomography::operator*(), vpColVector::operator*(), operator*(), vpRotationVector::operator,(), vpTranslationVector::operator,(), vpRotationMatrix::operator,(), vpHomogeneousMatrix::operator,(), vpRowVector::operator,(), vpColVector::operator,(), vpTranslationVector::operator-(), vpRowVector::operator-(), vpColVector::operator-(), vpTranslationVector::operator/(), vpRowVector::operator/(), vpHomography::operator/(), vpColVector::operator/(), vpHomography::operator/=(), vpRotationVector::operator<<(), vpTranslationVector::operator<<(), vpRotationMatrix::operator<<(), vpHomogeneousMatrix::operator<<(), vpRowVector::operator<<(), vpColVector::operator<<(), vpSubColVector::operator=(), vpSubRowVector::operator=(), vpQuaternionVector::operator=(), vpTranslationVector::operator=(), vpRotationMatrix::operator=(), vpRxyzVector::operator=(), vpRzyzVector::operator=(), vpRzyxVector::operator=(), vpRowVector::operator=(), vpThetaUVector::operator=(), vpColVector::operator=(), operator=(), vpRowVector::operator==(), vpColVector::operator==(), vpColVector::operator[](), qr(), qrPivot(), vpRowVector::reshape(), vpColVector::reshape(), vpQuaternionVector::set(), stack(), stackRows(), vpColVector::sum(), vpColVector::sumSquare(), svdEigen3(), svdLapack(), svdOpenCV(), vpRotationVector::t(), vpTranslationVector::t(), vpPoseVector::t(), vpRowVector::t(), vpColVector::t(), vpRotationVector::toStdVector(), vpRowVector::toStdVector(), vpColVector::toStdVector(), transpose(), vpColVector::vpColVector(), vpHomogeneousMatrix::vpHomogeneousMatrix(), vpMatrix(), vpRowVector::vpRowVector(), vpQuaternionVector::w(), vpQuaternionVector::x(), vpQuaternionVector::y(), vpQuaternionVector::z(), vpSubColVector::~vpSubColVector(), vpSubMatrix::~vpSubMatrix(), and vpSubRowVector::~vpSubRowVector().
|
protectedinherited |
Current array size (rowNum * colNum)
Definition at line 141 of file vpArray2D.h.
Referenced by vpColVector::clear(), frobeniusNorm(), hadamard(), inducedL2Norm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpRotationVector::operator*(), vpTranslationVector::operator*(), vpTranslationVector::operator-(), vpTranslationVector::operator/(), vpRotationMatrix::operator=(), vpRxyzVector::operator=(), vpRzyzVector::operator=(), vpRzyxVector::operator=(), vpThetaUVector::operator=(), vpRowVector::operator=(), vpColVector::operator=(), operator=(), vpRowVector::reshape(), vpColVector::reshape(), vpRotationVector::t(), vpColVector::vpColVector(), vpMatrix(), and vpRowVector::vpRowVector().
|
protectedinherited |
Number of rows in the array.
Definition at line 135 of file vpArray2D.h.
Referenced by AAt(), AtA(), vpColVector::clear(), detByLU(), detByLUEigen3(), detByLULapack(), detByLUOpenCV(), diag(), eigenValues(), expm(), vpColVector::extract(), eye(), getCol(), getDiag(), getRow(), vpColVector::hadamard(), hadamard(), vpColVector::infinityNorm(), infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), insert(), inverseByCholeskyLapack(), inverseByCholeskyOpenCV(), inverseByLU(), inverseByLUEigen3(), inverseByLULapack(), inverseByLUOpenCV(), inverseByQRLapack(), inverseTriangular(), vpTranslationVector::operator*(), vpRotationMatrix::operator*(), vpHomogeneousMatrix::operator*(), vpColVector::operator*(), operator*(), vpTranslationVector::operator*=(), vpRotationMatrix::operator*=(), vpColVector::operator*=(), operator*=(), vpColVector::operator+(), vpColVector::operator+=(), operator+=(), vpColVector::operator,(), vpColVector::operator-(), vpColVector::operator-=(), operator-=(), vpColVector::operator/(), operator/(), vpTranslationVector::operator/=(), vpColVector::operator/=(), operator/=(), vpColVector::operator<<(), operator<<(), vpSubColVector::operator=(), vpSubRowVector::operator=(), vpSubMatrix::operator=(), vpTranslationVector::operator=(), vpRowVector::operator=(), vpColVector::operator=(), operator=(), vpRowVector::operator==(), vpColVector::operator==(), qr(), qrPivot(), vpColVector::reshape(), setIdentity(), stack(), vpColVector::stack(), stackColumns(), stackRows(), vpColVector::sum(), sum(), vpRotationVector::sumSquare(), vpTranslationVector::sumSquare(), vpColVector::sumSquare(), sumSquare(), svdLapack(), vpTranslationVector::t(), vpPoseVector::t(), vpColVector::t(), transpose(), vpColVector::vpColVector(), vpMatrix(), and vpRowVector::vpRowVector().
|
protectedinherited |
Address of the first element of each rows.
Definition at line 139 of file vpArray2D.h.
Referenced by AAt(), vpColVector::clear(), infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpRowVector::init(), vpColVector::init(), init(), vpRotationMatrix::operator*(), vpForceTwistMatrix::operator*(), vpVelocityTwistMatrix::operator*(), vpHomogeneousMatrix::operator*(), operator*(), vpRotationMatrix::operator*=(), operator*=(), operator+=(), operator,(), operator-=(), operator/(), operator/=(), vpColVector::operator<<(), operator<<(), vpSubMatrix::operator=(), vpRotationMatrix::operator=(), vpForceTwistMatrix::operator=(), vpVelocityTwistMatrix::operator=(), vpHomogeneousMatrix::operator=(), vpRowVector::operator=(), vpColVector::operator=(), operator=(), stack(), stackColumns(), vpRowVector::sum(), sum(), vpRotationVector::sumSquare(), vpTranslationVector::sumSquare(), vpRowVector::sumSquare(), sumSquare(), vpColVector::vpColVector(), vpMatrix(), and vpRowVector::vpRowVector().