 |
ViSP
2.8.0
|
 |
ViSP
2.8.0
|
#include <vpHomography.h>
 Inheritance diagram for vpHomography:
Inheritance diagram for vpHomography:Public Types | |
| enum | vpDetMethod { LU_DECOMPOSITION } |
Public Member Functions | |
| vpHomography () | |
| vpHomography (const vpHomography &aMb) | |
| vpHomography (const vpHomogeneousMatrix &aMb, const vpPlane &bP) | |
| vpHomography (const vpRotationMatrix &aRb, const vpTranslationVector &atb, const vpPlane &bP) | |
| vpHomography (const vpThetaUVector &tu, const vpTranslationVector &atb, const vpPlane &bP) | |
| vpHomography (const vpPoseVector &arb, const vpPlane &bP) | |
| virtual | ~vpHomography () |
| void | buildFrom (const vpRotationMatrix &aRb, const vpTranslationVector &atb, const vpPlane &bP) |
| void | buildFrom (const vpThetaUVector &tu, const vpTranslationVector &atb, const vpPlane &bP) |
| void | buildFrom (const vpPoseVector &arb, const vpPlane &bP) |
| void | buildFrom (const vpHomogeneousMatrix &aMb, const vpPlane &bP) |
| void | build () |
| void | computeDisplacement (vpRotationMatrix &aRb, vpTranslationVector &atb, vpColVector &n) |
| void | computeDisplacement (const vpColVector &nd, vpRotationMatrix &aRb, vpTranslationVector &atb, vpColVector &n) |
| void | load (std::ifstream &f) |
| void | print () |
| void | save (std::ofstream &f) const |
| vpHomography | inverse () const |
| void | inverse (vpHomography &Hi) const |
| vpHomography | operator* (const vpHomography &H) const |
| vpHomography | operator* (const double &v) const |
| vpHomography | operator/ (const double &v) const |
| void | kill () |
| void | eye (unsigned int n) |
| void | eye (unsigned int m, unsigned int n) |
| void | setIdentity (const double &val=1.0) |
| void | stackMatrices (const vpMatrix &A) |
| void | insert (const vpMatrix &A, const unsigned int r, const unsigned int c) |
Columns, Rows extraction, Submatrix | |
| void | init (const vpMatrix &m, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) |
| vpRowVector | row (const unsigned int i) |
| vpColVector | column (const unsigned int j) |
Set/get Matrix size | |
| unsigned int | getRows () const |
| unsigned int | getCols () const |
| void | resize (const unsigned int nrows, const unsigned int ncols, const bool nullify=true) |
| double | getMinValue () const |
| double | getMaxValue () const |
Copy / assignment | |
| vpMatrix & | operator<< (double *) |
| void | diag (const vpColVector &A) |
Printing | |
| int | print (std::ostream &s, unsigned int length, char const *intro=0) |
| std::ostream & | matlabPrint (std::ostream &os) |
| std::ostream & | maplePrint (std::ostream &os) |
| std::ostream & | cppPrint (std::ostream &os, const char *matrixName=NULL, bool octet=false) |
| void | printSize () |
Access/modification operators | |
| double * | operator[] (unsigned int n) |
| double * | operator[] (unsigned int n) const |
Matrix operations | |
| vpMatrix & | operator+= (const vpMatrix &B) |
| vpMatrix & | operator+= (const double x) |
| vpMatrix & | operator-= (const vpMatrix &B) |
| vpMatrix & | operator-= (const double x) |
| vpMatrix | operator* (const vpMatrix &B) const |
| vpColVector | operator* (const vpColVector &b) const |
| vpTranslationVector | operator* (const vpTranslationVector &b) const |
| vpMatrix | operator* (const double x) const |
| vpMatrix | operator+ (const vpMatrix &B) const |
| vpMatrix | operator- (const vpMatrix &B) const |
| vpMatrix | operator- () const |
| vpMatrix & | operator*= (const double x) |
| vpMatrix & | operator/= (double x) |
| vpMatrix | operator/ (const double x) const |
| double | sumSquare () const |
| double | det (vpDetMethod method=LU_DECOMPOSITION) const |
| vpMatrix | expm () |
Transpose, Identity | |
| vpMatrix | t () const |
| vpMatrix | transpose () const |
| void | transpose (vpMatrix &C) const |
| vpMatrix | AAt () const |
| void | AAt (vpMatrix &B) const |
| vpMatrix | AtA () const |
| void | AtA (vpMatrix &B) const |
Kronecker product | |
| void | stackColumns (vpColVector &out) |
| vpColVector | stackColumns () |
| void | stackRows (vpRowVector &out) |
| vpRowVector | stackRows () |
| void | kron (const vpMatrix &m1, vpMatrix &out) |
| vpMatrix | kron (const vpMatrix &m1) |
Matrix inversion | |
| vpMatrix | inverseByLU () const |
| vpMatrix | inverseByCholesky () const |
| vpMatrix | inverseByCholeskyLapack () const |
| vpMatrix | inverseByQR () const |
| vpMatrix | inverseByQRLapack () const |
| vpMatrix | pseudoInverse (double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &ImA, vpMatrix &ImAt) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &ImA, vpMatrix &ImAt, vpMatrix &kerA) const |
SVD decomposition | |
| void | svd (vpColVector &w, vpMatrix &v) |
| void | solveBySVD (const vpColVector &B, vpColVector &x) const |
| vpColVector | solveBySVD (const vpColVector &B) const |
| unsigned int | kernel (vpMatrix &KerA, double svThreshold=1e-6) |
Eigen values | |
| vpColVector | eigenValues () |
| void | eigenValues (vpColVector &evalue, vpMatrix &evector) |
Norms | |
| double | euclideanNorm () const |
| double | infinityNorm () const |
Static Public Member Functions | |
| static void | HartleyNormalization (unsigned int n, double *x, double *y, double *xn, double *yn, double &xg, double &yg, double &coef) |
| static void | HartleyDenormalization (vpHomography &aHbn, vpHomography &aHb, double xg1, double yg1, double coef1, double xg2, double yg2, double coef2) |
| static void | build (vpHomography &aHb, const vpHomogeneousMatrix &aMb, const vpPlane &bP) |
| static void | DLT (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb) |
| static void | HartleyDLT (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb) |
| static void | HLM (unsigned int n, double *xb, double *yb, double *xa, double *ya, bool isplan, vpHomography &aHb) |
| static void | computeDisplacement (const vpHomography &aHb, const vpColVector &nd, vpRotationMatrix &aRb, vpTranslationVector &atb, vpColVector &n) |
| static void | computeDisplacement (const vpHomography &aHb, vpRotationMatrix &aRb, vpTranslationVector &atb, vpColVector &n) |
| static void | computeDisplacement (const vpMatrix &H, const double x, const double y, std::list< vpRotationMatrix > &vR, std::list< vpTranslationVector > &vT, std::list< vpColVector > &vN) |
| static double | computeDisplacement (unsigned int nbpoint, vpPoint *c1P, vpPoint *c2P, vpPlane &oN, vpHomogeneousMatrix &c2Mc1, vpHomogeneousMatrix &c1Mo, int userobust) |
| static double | computeDisplacement (unsigned int nbpoint, vpPoint *c1P, vpPoint *c2P, vpPlane *oN, vpHomogeneousMatrix &c2Mc1, vpHomogeneousMatrix &c1Mo, int userobust) |
| static double | computeResidual (vpColVector &x, vpColVector &M, vpColVector &d) |
| static double | computeRotation (unsigned int nbpoint, vpPoint *c1P, vpPoint *c2P, vpHomogeneousMatrix &c2Mc1, int userobust) |
| static void | computeTransformation (vpColVector &x, unsigned int *ind, vpColVector &M) |
| static bool | degenerateConfiguration (vpColVector &x, unsigned int *ind) |
| static bool | degenerateConfiguration (vpColVector &x, unsigned int *ind, double threshold_area) |
| static bool | ransac (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb, int consensus=1000, double threshold=1e-6) |
| static bool | ransac (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb, vpColVector &inliers, double &residual, int consensus=1000, double epsilon=1e-6, double areaThreshold=0.0) |
| static bool | saveMatrix (const char *filename, const vpMatrix &M, const bool binary=false, const char *Header="") |
| static bool | saveMatrix (std::string filename, const vpMatrix &M, const bool binary=false, const char *Header="") |
| static bool | loadMatrix (const char *filename, vpMatrix &M, const bool binary=false, char *Header=NULL) |
| static bool | loadMatrix (std::string filename, vpMatrix &M, const bool binary=false, char *Header=NULL) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | add2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | add2WeightedMatrices (const vpMatrix &A, const double &wA, const vpMatrix &B, const double &wB, vpMatrix &C) |
| static void | sub2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | negateMatrix (const vpMatrix &A, vpMatrix &C) |
| static void | multMatrixVector (const vpMatrix &A, const vpColVector &b, vpColVector &c) |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b) |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b, const vpMatrix &w) |
| static void | kron (const vpMatrix &m1, const vpMatrix &m2, vpMatrix &out) |
| static vpMatrix | kron (const vpMatrix &m1, const vpMatrix &m2) |
| static vpMatrix | stackMatrices (const vpMatrix &A, const vpMatrix &B) |
| static void | stackMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static vpMatrix | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B) |
| static void | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | createDiagonalMatrix (const vpColVector &A, vpMatrix &DA) |
| static vpMatrix | insert (const vpMatrix &A, const vpMatrix &B, const unsigned int r, const unsigned int c) |
| static void | insert (const vpMatrix &A, const vpMatrix &B, vpMatrix &C, const unsigned int r, const unsigned int c) |
Deprecated functions | |
| static vp_deprecated void | computeDisplacement (const vpMatrix H, const double x, const double y, vpList< vpRotationMatrix > &vR, vpList< vpTranslationVector > &vT, vpList< vpColVector > &vN) |
Public Attributes | |
| double * | data |
Protected Attributes | |
| unsigned int | rowNum |
| unsigned int | colNum |
| double ** | rowPtrs |
| unsigned int | dsize |
| unsigned int | trsize |
Related Functions | |
(Note that these are not member functions.) | |
| enum | vpGEMMmethod |
| vpMatrix | operator* (const double &x, const vpMatrix &B) |
| void | vpGEMM (const vpMatrix &A, const vpMatrix &B, const double &alpha, const vpMatrix &C, const double &beta, vpMatrix &D, const unsigned int &ops=0) |
| void | skew (const vpTranslationVector &t, vpMatrix &M) |
This class aims to compute the homography wrt.two images.
These two images are both described by a set of points. The 2 sets (one per image) are sets of corresponding points : for a point in a image, there is the corresponding point (image of the same 3D point) in the other image points set. These 2 sets are the only data needed to compute the homography. One method used is the one introduced by Ezio Malis during his PhD [9]. A normalization is carried out on this points in order to improve the conditioning of the problem, what leads to improve the stability of the result.
Store and compute the homography such that
![\[ ^a{\bf p} = ^a{\bf H}_b\; ^b{\bf p} \]](form_38.png)
with
![\[ ^a{\bf H}_b = ^a{\bf R}_b + \frac{^a{\bf t}_b}{^bd} { ^b{\bf n}^T} \]](form_37.png)
The example below shows how to manipulate this class to first compute a ground truth homography from camera poses, project pixel coordinates points using an homography and lastly estimate an homography from a subset of 4 matched points in frame a and frame b respectively.
Definition at line 173 of file vpHomography.h.
|
inherited |
Method used to compute the determinant of a square matrix.
| Enumerator | |
|---|---|
| LU_DECOMPOSITION |
LU decomposition method. |
Definition at line 103 of file vpMatrix.h.
| vpHomography::vpHomography | ( | ) |
initialize an homography as Identity
Definition at line 96 of file vpHomography.cpp.
| vpHomography::vpHomography | ( | const vpHomography & | aMb | ) |
copy constructor
initialize an homography from another homography
Definition at line 106 of file vpHomography.cpp.
| vpHomography::vpHomography | ( | const vpHomogeneousMatrix & | aMb, |
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
initialize an homography from another homography
Definition at line 116 of file vpHomography.cpp.
References buildFrom().
| vpHomography::vpHomography | ( | const vpRotationMatrix & | aRb, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 136 of file vpHomography.cpp.
References buildFrom().
| vpHomography::vpHomography | ( | const vpThetaUVector & | tu, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 128 of file vpHomography.cpp.
References buildFrom().
| vpHomography::vpHomography | ( | const vpPoseVector & | arb, |
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 144 of file vpHomography.cpp.
References buildFrom().
|
inlinevirtual |
Definition at line 233 of file vpHomography.h.
|
inherited |
Computes the 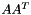 operation
operation 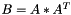
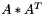
Definition at line 1248 of file vpMatrix.cpp.
|
inherited |
Compute the AAt operation such as 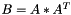 .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 1268 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
|
staticinherited |
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 493 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator+().
|
staticinherited |
Operation C = A*wA + B*wB
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 454 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Compute the AtA operation such as 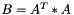
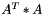
Definition at line 1359 of file vpMatrix.cpp.
Referenced by vpCalibration::calibrationTsai(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), and vpNurbs::globalCurveApprox().
|
inherited |
Compute the AtA operation such as 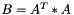 .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 1311 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrix::resize(), vpMatrix::rowNum, vpCERROR, and vpERROR_TRACE.
| void vpHomography::build | ( | ) |
build the homography from aMb and Rb
Compute aHb such that.
![\[ ^a{\bf H}_b = ^a{\bf R}_b + \frac{^a{\bf t}_b}{^bd} { ^b{\bf n}^T} \]](form_37.png)
Definition at line 429 of file vpHomography.cpp.
References vpPlane::getD(), vpPlane::getNormal(), and vpColVector::t().
Referenced by buildFrom().
|
static |
build the homography from aMb and Rb
Compute aHb such that.
![\[ ^a{\bf H}_b = ^a{\bf R}_b + \frac{^a{\bf t}_b}{^bd} { ^b{\bf n}^T} \]](form_37.png)
note d => -d verifier
Definition at line 459 of file vpHomography.cpp.
References vpPlane::getD(), vpPlane::getNormal(), and vpColVector::t().
| void vpHomography::buildFrom | ( | const vpRotationMatrix & | aRb, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 180 of file vpHomography.cpp.
References build().
Referenced by vpHomography().
| void vpHomography::buildFrom | ( | const vpThetaUVector & | tu, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 168 of file vpHomography.cpp.
References build().
| void vpHomography::buildFrom | ( | const vpPoseVector & | arb, |
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 192 of file vpHomography.cpp.
References build(), and vpHomogeneousMatrix::buildFrom().
| void vpHomography::buildFrom | ( | const vpHomogeneousMatrix & | aMb, |
| const vpPlane & | bP | ||
| ) |
Construction from homogeneous matrix and a plane.
Definition at line 155 of file vpHomography.cpp.
References build().
|
inherited |
Column extraction.
Return the ith columns of the matrix.
Definition at line 2240 of file vpMatrix.cpp.
References vpMatrix::getRows().
Referenced by DLT(), vpPose::poseDementhonPlan(), and vpPose::poseFromRectangle().
|
staticinherited |
Compute the covariance matrix of the parameters x from a least squares minimisation defined as: Ax = b
| A | : Matrix A from Ax = b. |
| x | : Vector x from Ax = b corresponding to the parameters to estimate. |
| b | : Vector b from Ax = b. |
Definition at line 56 of file vpMatrix_covariance.cpp.
References vpMatrix::pseudoInverse(), vpColVector::t(), and vpMatrix::t().
Referenced by vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpPose::poseVirtualVS(), and vpPose::poseVirtualVSrobust().
|
staticinherited |
Compute the covariance matrix of the parameters x from a least squares minimisation defined as: WAx = Wb
| A | : Matrix A from WAx = Wb. |
| x | : Vector x from WAx = Wb corresponding to the parameters to estimate. |
| b | : Vector b from WAx = Wb. |
| W | : Diagonal weigths matrix from WAx = Wb. |
Definition at line 74 of file vpMatrix_covariance.cpp.
References vpMatrix::pseudoInverse(), and vpMatrix::t().
| void vpHomography::computeDisplacement | ( | vpRotationMatrix & | aRb, |
| vpTranslationVector & | atb, | ||
| vpColVector & | n | ||
| ) |
Compute the camera displacement between two images from the homography 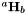 which is here an implicit parameter (*this).
which is here an implicit parameter (*this).
| aRb | : Rotation matrix as an output 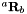 . . |
| atb | : Translation vector as an output 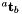 . . |
| n | : Normal vector to the plane as an output. |
Definition at line 671 of file vpHomographyExtract.cpp.
Referenced by computeDisplacement().
| void vpHomography::computeDisplacement | ( | const vpColVector & | nd, |
| vpRotationMatrix & | aRb, | ||
| vpTranslationVector & | atb, | ||
| vpColVector & | n | ||
| ) |
Compute the camera displacement between two images from the homography 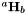 which is here an implicit parameter (*this).
which is here an implicit parameter (*this).
Camera displacement between 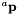 and
and 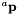 is represented as a rotation matrix
is represented as a rotation matrix 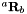 and a translation vector
and a translation vector 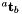 from which an homogenous matrix can be build (vpHomogeneousMatrix).
from which an homogenous matrix can be build (vpHomogeneousMatrix).
| nd | : Input normal vector to the plane used to compar with the normal vector n extracted from the homography. |
| aRb | : Rotation matrix as an output 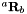 . . |
| atb | : Translation vector as an output 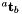 . . |
| n | : Normal vector to the plane as an output. |
Definition at line 366 of file vpHomographyExtract.cpp.
References computeDisplacement().
|
static |
Compute the camera displacement between two images from the homography 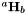 .
.
Camera displacement between 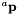 and
and 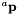 is represented as a rotation matrix
is represented as a rotation matrix 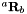 and a translation vector
and a translation vector 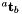 from which an homogenous matrix can be build (vpHomogeneousMatrix).
from which an homogenous matrix can be build (vpHomogeneousMatrix).
| aHb | : Input homography 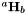 . . |
| nd | : Input normal vector to the plane used to compar with the normal vector n extracted from the homography. |
| aRb | : Rotation matrix as an output 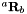 . . |
| atb | : Translation vector as an output 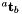 . . |
| n | : Normal vector to the plane as an output. |
Definition at line 76 of file vpHomographyExtract.cpp.
References vpMatrix::det(), vpRotationMatrix::isARotationMatrix(), vpColVector::resize(), vpMatrix::svd(), and vpColVector::t().
|
static |
Compute the camera displacement between two images from the homography 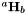 .
.
Camera displacement between 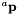 and
and 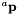 is represented as a rotation matrix
is represented as a rotation matrix 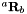 and a translation vector
and a translation vector 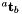 from which an homogenous matrix can be build (vpHomogeneousMatrix).
from which an homogenous matrix can be build (vpHomogeneousMatrix).
| aHb | : Input homography 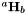 . . |
| aRb | : Rotation matrix as an output 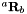 . . |
| atb | : Translation vector as an output 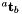 . . |
| n | : Normal vector to the plane as an output. |
Definition at line 392 of file vpHomographyExtract.cpp.
References vpMatrix::det(), vpRotationMatrix::isARotationMatrix(), vpColVector::resize(), vpMatrix::svd(), and vpColVector::t().
|
static |
Definition at line 684 of file vpHomographyExtract.cpp.
References vpRotationMatrix::setIdentity(), vpMath::sqr(), vpMatrix::svd(), and vpRotationMatrix::t().
|
static |
Definition at line 301 of file vpHomographyVVS.cpp.
References vpExponentialMap::direct(), vpMath::equal(), vpHomogeneousMatrix::extract(), vpPoint::get_x(), vpPoint::get_y(), vpHomogeneousMatrix::inverse(), vpRobust::MEstimator(), vpMatrix::pseudoInverse(), vpRobust::setIteration(), vpRobust::setThreshold(), vpTranslationVector::skew(), vpMath::sqr(), vpMatrix::stackMatrices(), vpMatrix::sumSquare(), vpColVector::t(), vpRobust::TUKEY, and vpMatrix::vpMatrix().
|
static |
Definition at line 521 of file vpHomographyVVS.cpp.
References vpExponentialMap::direct(), vpMath::equal(), vpHomogeneousMatrix::extract(), vpPoint::get_x(), vpPoint::get_y(), vpHomogeneousMatrix::inverse(), vpRobust::MEstimator(), vpMatrix::pseudoInverse(), vpRobust::setIteration(), vpRobust::setThreshold(), vpTranslationVector::skew(), vpMath::sqr(), vpMatrix::stackMatrices(), vpMatrix::sumSquare(), vpColVector::t(), vpRobust::TUKEY, and vpMatrix::vpMatrix().
|
static |
Definition at line 1342 of file vpHomographyExtract.cpp.
References vpList< type >::addRight(), vpList< type >::kill(), vpRotationMatrix::setIdentity(), vpMath::sqr(), vpMatrix::svd(), and vpRotationMatrix::t().
|
static |
Definition at line 193 of file vpHomographyRansac.cpp.
References vpMatrix::data, vpMatrix::getRows(), vpColVector::resize(), and vpMatrix::sumSquare().
|
static |
Definition at line 102 of file vpHomographyVVS.cpp.
References vpMath::equal(), vpPoint::get_x(), vpPoint::get_y(), vpMath::maximum(), vpRobust::MEstimator(), vpMatrix::pseudoInverse(), vpRobust::setIteration(), vpRobust::setThreshold(), vpMath::sqr(), vpMatrix::stackMatrices(), vpMatrix::sumSquare(), vpMatrix::t(), and vpRobust::TUKEY.
|
static |
Definition at line 154 of file vpHomographyRansac.cpp.
References vpMatrix::data, vpMatrix::getRows(), HLM(), vpColVector::resize(), and vpMatrix::setIdentity().
|
inherited |
Print to be used as part of a C++ code later.
Print under the following form: vpMatrix A(6,4); A[0][0] = 1.4; A[0][1] = 0.6; ...
| os | the stream to be printed in. |
| matrixName | name of the matrix, "A" by default, to be used for the line vpMatrix A(6,7) (see example). |
| octet | if false, print using double, if true, print byte per byte each bytes of the double array. |
Definition at line 2768 of file vpMatrix.cpp.
References vpMatrix::getRows().
|
staticinherited |
Create a diagonal matrix with the element of a vector 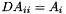 .
.
| A | : Vector which element will be put in the diagonal. |
| DA | : Diagonal matrix DA[i][i] = A[i] |
Definition at line 2551 of file vpMatrix.cpp.
References vpMatrix::getRows(), vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
|
static |
Definition at line 121 of file vpHomographyRansac.cpp.
References vpMatrix::getRows().
|
static |
Definition at line 48 of file vpHomographyRansac.cpp.
References vpMatrix::getRows().
|
inherited |
Compute the determinant of a n-by-n matrix.
| method | : Method used to compute the determinant. Default LU decomposition methos is faster than the method based on Gaussian elimination. |
Definition at line 3413 of file vpMatrix.cpp.
References vpMatrix::LU_DECOMPOSITION.
Referenced by computeDisplacement().
|
inherited |
Create a diagonal matrix with the element of a vector.
| A | : Vector which element will be put in the diagonal. |
Definition at line 2523 of file vpMatrix.cpp.
References vpMatrix::getRows(), vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
Referenced by vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), and vpMbEdgeTracker::computeVVS().
|
static |
Computes the homography matrix wrt. the data using the DLT (Direct Linear Transform) algorithm.
Computes H such as
![\[ ^a{\bf p} = ^a{\bf H}_b\; ^b{\bf p} \]](form_38.png)
To do so, we use the DLT algorithm on the data, ie we resolve the linear system by SDV : 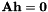 .
. 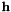 is the vector with the terms of
is the vector with the terms of 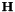 ,
,
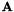 depends on the points coordinates.
depends on the points coordinates.
At least 4 correspondant points couples are needed.
For each point, in homogeneous coordinates we have:
![\[ \mathbf{p}_{a}= \mathbf{H}\mathbf{p}_{b} \]](form_43.png)
which is equivalent to:
![\[ \mathbf{p}_{a} \times \mathbf{H}\mathbf{p}_{b} =0 \]](form_44.png)
If we note 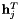 the
the 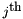 line of
line of 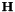 , we can write:
, we can write:
![\[ \mathbf{H}\mathbf{p}_{b} = \left( \begin{array}{c}\mathbf{h}_1^T\mathbf{p}_{b} \\\mathbf{h}_2^T\mathbf{p}_{b} \\\mathbf{h}_3^T \mathbf{p}_{b} \end{array}\right) \]](form_47.png)
Setting 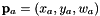 , the cross product can be rewritten by:
, the cross product can be rewritten by:
![\[ \mathbf{p}_{a} \times \mathbf{H}\mathbf{p}_{b} =\left( \begin{array}{c}y_{a}\mathbf{h}_3^T\mathbf{p}_{b}-w_{a}\mathbf{h}_2^T\mathbf{p}_{b} \\w_{a}\mathbf{h}_1^T\mathbf{p}_{b} -x_{a}\mathbf{h}_3^T \mathbf{p}_{b} \\x_{a}\mathbf{h}_2^T \mathbf{p}_{b}- y_{a}\mathbf{h}_1^T\mathbf{p}_{b}\end{array}\right) \]](form_49.png)
![\[ \underbrace{\left( \begin{array}{ccc}\mathbf{0}^T & -w_{a} \mathbf{p}_{b}^T & y_{a} \mathbf{p}_{b}^T \\ w_{a} \mathbf{p}_{b}^T&\mathbf{0}^T & -x_{a} \mathbf{p}_{b}^T \\ -y_{a} \mathbf{p}_{b}^T & x_{a} \mathbf{p}_{b}^T & \mathbf{0}^T\end{array}\right)}_{\mathbf{A}_i (3\times 9)} \underbrace{\left( \begin{array}{c}\mathbf{h}_{1}^{T} \\ \mathbf{h}_{2}^{T}\\\mathbf{h}_{3}^{T}\end{array}\right)}_{\mathbf{h} (9\times 1)}=0 \]](form_50.png)
leading to an homogeneous system to be solve: 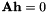 with
with 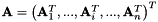 .
.
It can be solved using an SVD decomposition:
![\[\bf A = UDV^T \]](form_53.png)
h is the column of V associated with the smalest singular value of A
| vpMatrixException::rankDeficient | : When the rank of the matrix that should be 8 is deficient. |
Definition at line 269 of file vpHomographyDLT.cpp.
References vpMatrix::column(), vpMatrixException::rankDeficient, vpMatrix::resize(), vpMatrix::svd(), vpERROR_TRACE, and vpTRACE.
Referenced by HartleyDLT().
|
inherited |
Compute the eigenvalues of a n-by-n real symmetric matrix.
| vpMatrixException::matrixError | If the matrix is not square or if the matrix is not symmetric. |
| vpMatrixException::notImplementedError | If the GSL library is not detected |
Here an example:
Definition at line 2996 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::matrixError, vpMatrixException::notImplementedError, vpMatrix::rowNum, vpMatrix::t(), and vpERROR_TRACE.
|
inherited |
Compute the eigenvalues of a n-by-n real symmetric matrix.
| evalue | : Eigenvalues of the matrix. |
| evector | : Eigenvector of the matrix. |
| vpMatrixException::matrixError | If the matrix is not square or if the matrix is not symmetric. |
| vpMatrixException::notImplementedError | If the GSL library is not detected |
Here an example:
Definition at line 3115 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrixException::matrixError, vpMatrixException::notImplementedError, vpColVector::resize(), vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::t(), and vpERROR_TRACE.
|
inherited |
Compute and return the Euclidean norm 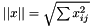 .
.
Definition at line 2816 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::dsize.
Referenced by vpSimulatorAfma6::setPosition().
|
inherited |
Compute the exponential matrix of a square matrix.
Definition at line 3600 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::incorrectMatrixSizeError, vpMatrix::inverseByLU(), vpMatrix::rowNum, vpMatrix::setIdentity(), and vpTRACE.
|
inherited |
Set an n-by-n matrix to identity.
eye(n) is an n-by-n matrix with ones on the diagonal and zeros else where.
Definition at line 1132 of file vpMatrix.cpp.
References vpCERROR, and vpERROR_TRACE.
Referenced by vpServo::setServo().
|
inherited |
Set an m-by-n matrix to identity.
eye(m,n) is an m-by-n matrix with ones on the diagonal and zeros else where.
Definition at line 1152 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpCERROR, and vpERROR_TRACE.
|
inlineinherited |
Return the number of columns of the matrix.
Definition at line 159 of file vpMatrix.h.
Referenced by vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpSubRowVector::checkParentStatus(), vpSubMatrix::checkParentStatus(), vpServo::computeControlLaw(), vpServo::computeInteractionMatrix(), vpMbTracker::computeJTR(), vpImageSimulator::getImage(), vpSubRowVector::init(), vpSubMatrix::init(), vpCameraParameters::initFromCalibrationMatrix(), vpMatrix::insert(), vpMatrix::inverseByCholeskyLapack(), vpMatrix::inverseByQRLapack(), vpMatrix::juxtaposeMatrices(), vpMatrix::kernel(), vpMatrix::kron(), vpMatrix::maplePrint(), vpRowVector::operator*(), vpRotationMatrix::operator*(), vpVelocityTwistMatrix::operator*(), vpForceTwistMatrix::operator*(), vpMatrix::operator*(), vpMatrix::operator+=(), vpMatrix::operator-=(), vpSubRowVector::operator=(), vpRowVector::operator=(), vpSubColVector::operator=(), vpSubMatrix::operator=(), vpRotationMatrix::operator=(), vpColVector::operator=(), vpPose::poseDementhonPlan(), vpMatrix::print(), vpMatrix::pseudoInverse(), vpIoTools::readConfigVar(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::row(), vpMatrix::saveMatrix(), vpServo::secondaryTask(), vpRowVector::size(), vpMatrix::stackMatrices(), vpMatrix::sub2Matrices(), and vpMatrix::svd().
|
inherited |
Definition at line 3685 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::dsize.
|
inherited |
Definition at line 3671 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::dsize.
|
inlineinherited |
Return the number of rows of the matrix.
Definition at line 157 of file vpMatrix.h.
Referenced by vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpLine::changeFrame(), vpSubColVector::checkParentStatus(), vpSubMatrix::checkParentStatus(), vpMatrix::column(), vpServo::computeError(), vpServo::computeInteractionMatrix(), vpMbTracker::computeJTR(), vpPtu46::computeMGD(), vpPose::computeResidual(), computeResidual(), computeTransformation(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpMatrix::cppPrint(), vpMatrix::createDiagonalMatrix(), vpColVector::crossProd(), vpDot2::defineDots(), degenerateConfiguration(), vpMatrix::diag(), vpProjectionDisplay::display(), vpColVector::dotProd(), vpGenericFeature::error(), vpImageFilter::filter(), vpPtu46::get_eJe(), vpBiclops::get_eJe(), vpPtu46::get_fJe(), vpBiclops::get_fJe(), vpBiclops::get_fMe(), vpGenericFeature::get_s(), vpBasicFeature::getDimension(), vpImageSimulator::getImage(), vpAfma6::getInverseKinematics(), vpViper::getInverseKinematicsWrist(), vpSubColVector::init(), vpSubMatrix::init(), vpCameraParameters::initFromCalibrationMatrix(), vpMatrix::insert(), vpFeatureLuminance::interaction(), vpGenericFeature::interaction(), vpMatrix::inverseByCholeskyLapack(), vpMatrix::inverseByLU(), vpMatrix::inverseByQRLapack(), vpColVector::invSort(), vpMatrix::juxtaposeMatrices(), vpMatrix::kernel(), vpScale::KernelDensity(), vpScale::KernelDensityGradient(), vpMatrix::kron(), vpMatrix::maplePrint(), vpMatrix::matlabPrint(), vpColVector::mean(), vpScale::MeanShift(), vpColVector::median(), vpRobust::MEstimator(), vpMatrix::multMatrixVector(), vpRowVector::operator*(), vpRotationMatrix::operator*(), vpVelocityTwistMatrix::operator*(), vpForceTwistMatrix::operator*(), vpMatrix::operator*(), vpMatrix::operator+=(), vpMatrix::operator-=(), vpColVector::operator<<(), vpSubColVector::operator=(), vpSubMatrix::operator=(), vpSubRowVector::operator=(), vpRotationMatrix::operator=(), vpColVector::operator=(), vpRGBa::operator=(), vpPlot::plot(), vpPose::poseDementhonPlan(), vpPose::poseVirtualVSrobust(), vpKalmanFilter::prediction(), vpMatrix::print(), vpLine::projection(), vpMatrix::pseudoInverse(), vpIoTools::readConfigVar(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::saveMatrix(), vpGenericFeature::set_s(), vpGenericFeature::setError(), vpGenericFeature::setInteractionMatrix(), vpSimulatorAfma6::setJointLimit(), vpSimulatorViper850::setJointLimit(), vpRobotBiclopsController::setPosition(), vpRobotAfma4::setPosition(), vpRobotBiclopsController::setVelocity(), vpRobotPtu46::setVelocity(), vpRobotBiclops::setVelocity(), vpSimulatorAfma6::setVelocity(), vpSimulatorViper850::setVelocity(), vpRobotAfma4::setVelocity(), vpLine::setWorldCoordinates(), vpRobust::simultMEstimator(), vpColVector::size(), vpColVector::skew(), vpColVector::sort(), vpColVector::stack(), vpMatrix::stackMatrices(), vpMatrix::sub2Matrices(), vpMatrix::svd(), and vpColVector::vpColVector().
|
static |
Definition at line 107 of file vpHomographyDLT.cpp.
References vpMatrix::pseudoInverse(), vpMatrix::setIdentity(), and vpMatrix::vpMatrix().
Referenced by HartleyDLT().
|
static |
Computes the homography matrix using the DLT (Direct Linear Transform) algorithm on normalized data.
Normalizes data, computes H wrt. these normalized data and denormalizes the result. The normalization carried out is the one preconized by Hartley . At least 4 correspondant points couples are needed.
| vpMatrixException::rankDeficient | : When the rank of the matrix that should be 8 is deficient. |
Definition at line 159 of file vpHomographyDLT.cpp.
References DLT(), HartleyDenormalization(), HartleyNormalization(), and vpTRACE.
|
static |
Definition at line 57 of file vpHomographyDLT.cpp.
References vpMath::sqr().
Referenced by HartleyDLT().
|
static |
Computes the homography matrix from planar [9] or non planar points using Ezio Malis linear method (HLM) [8].
Computes H such as
![\[ ^a{\bf p} = ^a{\bf H}_b\; ^b{\bf p} \]](form_38.png)
The algorithm for 2D scene implemented in this file is described in Ezio Malis PhD thesis.
If the boolean isplanar is true the point is assumed to be in a plane otherwise there are assumed to be planar.
The reference planar is the plane build from the 3 first points.
Definition at line 714 of file vpHomographyMalis.cpp.
References vpMatrix::setIdentity().
Referenced by computeTransformation(), and vpPose::poseFromRectangle().
|
inherited |
Compute and return the infinity norm 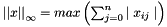 with
with 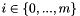 where
where 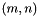 is the matrix size.
is the matrix size.
Definition at line 2840 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
|
inherited |
subvpMatrix extraction
Definition at line 263 of file vpMatrix.cpp.
References vpMatrix::resize(), and vpERROR_TRACE.
|
inherited |
Insert matrix A at the given position in the current matrix.
| A | : The matrix to insert. |
| r | : The index of the row to begin to insert data. |
| c | : The index of the column to begin to insert data. |
Definition at line 2939 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, and vpMatrix::rowNum.
Referenced by vpNurbs::curveKnotIns(), vpMatrix::insert(), vpPioneerPan::set_mMp(), and vpPioneerPan::set_pMe().
|
staticinherited |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| r | : Index of the row where to add the matrix. |
| c | : Index of the column where to add the matrix. |
Definition at line 2348 of file vpMatrix.cpp.
References vpMatrix::insert(), and vpCERROR.
|
staticinherited |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| C | : Result matrix. |
| r | : Index of the row where to insert matrix B. |
| c | : Index of the column where to insert matrix B. |
Definition at line 2379 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
| vpHomography vpHomography::inverse | ( | ) | const |
invert the homography
Definition at line 274 of file vpHomography.cpp.
References vpMatrix::pseudoInverse().
Referenced by inverse().
| void vpHomography::inverse | ( | vpHomography & | bHa | ) | const |
invert the homography
| bHa | : [H]^-1 |
Definition at line 291 of file vpHomography.cpp.
References inverse().
|
inherited |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition. The matrix must be real and symmetric. Only available if lapack is installed.
Here an example:
Definition at line 124 of file vpMatrix_cholesky.cpp.
References vpMatrix::colNum, vpMatrix::inverseByCholeskyLapack(), vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
|
inherited |
Definition at line 62 of file vpMatrix_cholesky.cpp.
References vpException::badValue, vpMatrix::data, vpMatrix::getCols(), vpMatrix::getRows(), and vpMatrix::rowNum.
Referenced by vpMatrix::inverseByCholesky().
|
inherited |
Compute the inverse of a n-by-n matrix using the LU decomposition.
Here an example:
Definition at line 236 of file vpMatrix_lu.cpp.
References vpMatrix::colNum, vpMatrix::getRows(), vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
Referenced by vpMatrix::expm(), and vpKalmanFilter::filtering().
|
inherited |
Compute the inverse of a n-by-n matrix using the QR decomposition. Only available if lapack is installed.
Here an example:
Definition at line 226 of file vpMatrix_qr.cpp.
References vpMatrix::colNum, vpMatrix::inverseByQRLapack(), vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
|
inherited |
Definition at line 73 of file vpMatrix_qr.cpp.
References vpException::badValue, vpMatrix::colNum, vpMatrix::data, vpMatrix::getCols(), vpMatrix::getRows(), and vpMatrix::rowNum.
Referenced by vpMatrix::inverseByQR().
Juxtapose to matrices C = [ A B ].
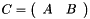
| A | : Left matrix. |
| B | : Right matrix. |
Definition at line 2422 of file vpMatrix.cpp.
References vpCERROR.
Juxtapose to matrices C = [ A B ].
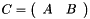
| A | : Left matrix. |
| B | : Right matrix. |
| C | : Juxtaposed matrix C = [ A B ] |
Definition at line 2451 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
|
inherited |
Function to compute the null space (the kernel) of the interaction matrix A which is not full rank. The null space ( the kernel ) of a matrix A is defined as Null(A) = Ker(M) ={KerA : A*KerA =0}.
| kerA | : The matrix to contain the null space (kernel) of A (A*KerA.t()=0) |
| svThreshold | : Specify the used threshold in the svd(...) function (a function to compute the singular value decomposition) |
Definition at line 3217 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrix::resize(), vpMatrix::row(), vpMatrix::sumSquare(), and vpMatrix::svd().
|
inherited |
Destruction of the matrix (Memory de-allocation)
Definition at line 286 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::rowPtrs.
Referenced by vpMatrix::~vpMatrix().
Compute Kronecker product matrix.
| m | : vpMatrix. |
| out | : If m1.kron(m2) out contains the kronecker product's result :  . . |
Definition at line 1477 of file vpMatrix.cpp.
Referenced by vpMatrix::kron().
Compute Kronecker product matrix.
| m | : vpMatrix; |

Definition at line 1518 of file vpMatrix.cpp.
References vpMatrix::kron().
Compute Kronecker product matrix.
Definition at line 1443 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::rowNum, and vpERROR_TRACE.
Compute Kronecker product matrix.

Definition at line 1487 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
| void vpHomography::load | ( | std::ifstream & | f | ) |
Load an homography from a file.
Read an homography in a file, verify if it is really an homogeneous matrix.
| f | : the file. |
Definition at line 395 of file vpHomography.cpp.
References vpException::ioError, and vpERROR_TRACE.
|
staticinherited |
Load a matrix to a file.
| filename | : Absolute file name. |
| M | : Matrix to be loaded. |
| binary | : If true the matrix is loaded from a binary file, else from a text file. |
| Header | : Header of the file loaded in this parameter. |
Definition at line 3513 of file vpMatrix.cpp.
References vpMatrix::resize().
Referenced by vpDot2::defineDots(), and vpMatrix::loadMatrix().
|
inlinestaticinherited |
Load a matrix to a file.
| filename | : absolute file name |
| M | : matrix to be loaded |
| binary | :If true the matrix is load from a binary file, else from a text file. |
| Header | : Header of the file is load in this parameter |
Definition at line 218 of file vpMatrix.h.
References vpMatrix::loadMatrix().
|
inherited |
Print using MAPLE matrix input format.
Print using the following way so that this output can be directly copied into MAPLE: ([ [0.939846, 0.0300754, 0.340272, ], [0.0300788, 0.984961, -0.170136, ], [-0.340272, 0.170136, 0.924807, ], ])
Definition at line 2735 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
|
inherited |
Print using matlab syntax, to be put in matlab later.
Print using the following form: [ a,b,c; d,e,f; g,h,i]
Definition at line 2706 of file vpMatrix.cpp.
References vpMatrix::getRows().
|
staticinherited |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 393 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator*().
|
staticinherited |
Operation c = A * b (c and b are vectors).
The result is placed in the second parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 811 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpColVector::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpRotationMatrix::operator*(), and vpMatrix::operator*().
Operation C = -A.
The result is placed in the second parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 709 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator-().
| vpHomography vpHomography::operator* | ( | const vpHomography & | H | ) | const |
Multiplication by an homography.
| H | : Homography to multiply with. |
Definition at line 324 of file vpHomography.cpp.
Operation C = A * B (A is unchanged).
Definition at line 436 of file vpMatrix.cpp.
References vpMatrix::mult2Matrices().
| vpHomography vpHomography::operator* | ( | const double & | v | ) | const |
Multiply an homography by a scalar.
| v | : Value of the scalar. |
Definition at line 353 of file vpHomography.cpp.
References vpMatrix::data.
|
inherited |
Operation c = A * b (A is unchanged, c and b are vectors).
Definition at line 846 of file vpMatrix.cpp.
References vpMatrix::multMatrixVector().
|
inherited |
Operation c = A * b (A is unchanged, c and b are translation vectors).
Definition at line 855 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::incorrectMatrixSizeError, vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Cij = Aij * x (A is unchanged)
Definition at line 930 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Multiply all the element of the matrix by x : Aij = Aij * x.
Definition at line 1058 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
Operation C = A + B (A is unchanged).
Definition at line 544 of file vpMatrix.cpp.
References vpMatrix::add2Matrices().
Operation A = A + B.
Definition at line 624 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Add x to all the element of the matrix : Aij = Aij + x.
Definition at line 1010 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
Operation C = A - B (A is unchanged).
Definition at line 615 of file vpMatrix.cpp.
References vpMatrix::sub2Matrices().
|
inherited |
Operation C = -A (A is unchanged).
Definition at line 751 of file vpMatrix.cpp.
References vpMatrix::negateMatrix().
Operation A = A - B.
Definition at line 664 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Substract x to all the element of the matrix : Aij = Aij - x.
Definition at line 1034 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
| vpHomography vpHomography::operator/ | ( | const double & | v | ) | const |
Divide an homography by a scalar.
| v | : Value of the scalar. |
Definition at line 377 of file vpHomography.cpp.
References vpMatrix::data.
|
inherited |
Cij = Aij / x (A is unchanged)
Definition at line 965 of file vpMatrix.cpp.
References vpMatrix::colNum, vpException::divideByZeroError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
|
inherited |
Divide all the element of the matrix by x : Aij = Aij / x.
Definition at line 1073 of file vpMatrix.cpp.
References vpMatrix::colNum, vpException::divideByZeroError, vpMatrix::rowNum, and vpMatrix::rowPtrs.
|
inherited |
Assigment from an array of double.
Definition at line 368 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
|
inlineinherited |
write elements Aij (usage : A[i][j] = x )
Definition at line 248 of file vpMatrix.h.
|
inlineinherited |
read elements Aij (usage : x = A[i][j] )
Definition at line 250 of file vpMatrix.h.
|
inherited |
Pretty print a matrix. The data are tabulated. The common widths before and after the decimal point are set with respect to the parameter maxlen.
| s | Stream used for the printing. |
| length | The suggested width of each matrix element. The actual width grows in order to accomodate the whole integral part, and shrinks if the whole extent is not needed for all the numbers. |
| intro | The introduction which is printed before the matrix. Can be set to zero (or omitted), in which case the introduction is not printed. |
Definition at line 2615 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), and vpMath::maximum().
| void vpHomography::print | ( | ) |
Print the matrix.
Print the matrix as a vector [T thetaU].
Definition at line 416 of file vpHomography.cpp.
|
inlineinherited |
Definition at line 183 of file vpMatrix.h.
|
inherited |
Compute the pseudo inverse of the matrix using the SVD.
Compute and return the pseudo inverse of a n-by-m matrix : 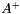 .
.
| svThreshold | : Threshold used to test the singular values. |
Here an example to compute the inverse of a n-by-n matrix. If the matrix is n-by-n it is also possible to use inverseByLU().
Definition at line 1812 of file vpMatrix.cpp.
Referenced by vpCalibration::calibrationTsai(), vpSimulatorAfma6::computeArticularVelocity(), vpSimulatorViper850::computeArticularVelocity(), vpServo::computeControlLaw(), vpMatrix::computeCovarianceMatrix(), computeDisplacement(), computeRotation(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpNurbs::globalCurveApprox(), vpNurbs::globalCurveInterp(), HartleyDenormalization(), vpMeEllipse::initTracking(), inverse(), vpMeLine::leastSquare(), vpPose::poseDementhonNonPlan(), vpPose::poseFromRectangle(), vpPose::poseVirtualVS(), vpMatrix::pseudoInverse(), and vpMatrix::solveBySVD().
|
inherited |
Compute the pseudo inverse of the matrix 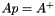 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank
| Ap | : The pseudo inverse 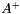 . . |
| svThreshold | : Threshold used to test the singular values. |
Definition at line 1772 of file vpMatrix.cpp.
References vpMatrix::pseudoInverse().
|
inherited |
Compute the pseudo inverse of the matrix 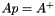 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank and the singular value
| Ap | : The pseudo inverse 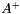 . . |
| sv | : Singular values. |
| svThreshold | : Threshold used to test the singular values. |
Definition at line 1828 of file vpMatrix.cpp.
References vpMatrix::pseudoInverse().
|
inherited |
Compute the pseudo inverse of the matrix 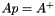 along with Ker A, Ker
along with Ker A, Ker 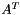 , Im A and Im
, Im A and Im 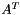 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank and the singular value, image
Pseudo inverse, kernel and image are computed using the SVD decomposition.
A is an m x n matrix, if m >=n the svd works on A other wise it works on 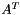 .
.
Therefore if m>=n we have
![\[ {\bf A}_{m\times n} = {\bf U}_{m\times m} {\bf S}_{m\times n} {\bf V^\top}_{n\times n} \]](form_191.png)
![\[ {\bf A}_{m\times n} = \left[\begin{array}{ccc}\mbox{Im} {\bf A} & | & \mbox{Ker} {\bf A^\top} \end{array} \right] {\bf S} \left[ \begin{array}{c} (\mbox{Im} {\bf A^\top})^\top \\ (\mbox{Ker}{\bf A})^\top \end{array}\right] \]](form_192.png)
where Im(A) is an m x r matrix (r is the rank of A) and Im(A^T) is an r x n matrix
| Ap | : The pseudo inverse 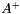 . . |
| sv | : Singular values. |
| svThreshold | : Threshold used to test the singular values. |
| imAt | : Image A^T |
| imA | Image A |
Definition at line 1867 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpColVector::resize(), vpMatrix::resize(), vpMatrix::svd(), and vpMatrix::t().
|
inherited |
Compute the pseudo inverse of the matrix 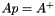 along with Ker A, Ker
along with Ker A, Ker 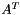 , Im A and Im
, Im A and Im 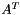 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank and the singular value, image, kernel.
Pseudo inverse, kernel and image are computed using the SVD decomposition.
A is an m x n matrix, if m >=n the svd works on A other wise it works on 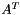 .
.
Therefore if m>=n we have
![\[ {\bf A}_{m\times n} = {\bf U}_{m\times m} {\bf S}_{m\times n} {\bf V^\top}_{n\times n} \]](form_191.png)
![\[ {\bf A}_{m\times n} = \left[\begin{array}{ccc}\mbox{Im} {\bf A} & | & \mbox{Ker} {\bf A^\top} \end{array} \right] {\bf S} \left[ \begin{array}{c} (\mbox{Im} {\bf A^\top})^\top \\ (\mbox{Ker}{\bf A})^\top \end{array}\right] \]](form_192.png)
where Im(A) is an m x r matrix (r is the rank of A) and Im(A^T) is an r x n matrix
| Ap | : The pseudo inverse 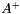 . . |
| sv | : Singular values. |
| svThreshold | : Threshold used to test the singular values. |
| imA | Image A |
| imAt | : Image A^T |
| kerA | : null space of A |
Definition at line 2045 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpColVector::resize(), vpMatrix::resize(), vpMatrix::row(), vpMatrix::sumSquare(), vpMatrix::svd(), and vpMatrix::t().
|
static |
Definition at line 265 of file vpHomographyRansac.cpp.
References vpMatrix::data, and vpRansac< vpTransformation >::ransac().
|
static |
Computes homography matrix 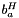 such as
such as 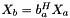 with
with 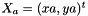 and
and 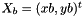 .
.
| n | : Number of points. |
| xb,yb | : Coordinates of the points in 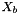 vector. vector. |
| xa,ya | : Coordinates of the points in 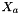 vector. vector. |
| bHa | : Homography matrix computed from 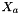 and and 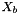 vectors. vectors. |
| inliers | : n dimention vector indicating if a point is an inlier (value 1.0) or an outlier (value 0). Matches are stocked in inliers vector column. |
| residual | : Residual. Not used. |
| consensus | : Minimal number of points (less than n) fitting the model. |
| threshold | : Threshold for outlier removing. |
| areaThreshold | : Ensure that the area formed by every 3 points within the 4 points used to compute the homography is greater than this threshold. If the area is smaller, we are in a degenerate case. |
Definition at line 323 of file vpHomographyRansac.cpp.
References vpMatrix::data, and vpRansac< vpTransformation >::ransac().
|
inherited |
Set the size of the matrix and initialize all the values to zero.
| nrows | : number of rows |
| ncols | : number of column |
| flagNullify | : if true, then the matrix is re-initialized to 0 after resize. If false, the initial values from the common part of the matrix (common part between old and new version of the matrix) are kept. Default value is true. |
Definition at line 174 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrix::dsize, vpException::memoryAllocationError, vpMatrix::rowNum, vpMatrix::rowPtrs, vpMatrix::t(), vpMatrix::trsize, vpCDEBUG, vpDEBUG_TRACE, and vpERROR_TRACE.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::AtA(), vpServo::computeControlLaw(), vpMbTracker::computeJTR(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMatrix::createDiagonalMatrix(), vpMatrix::diag(), vpProjectionDisplay::display(), DLT(), vpMatrix::eigenValues(), vpMatrix::eye(), vpPtu46::get_eJe(), vpAfma4::get_eJe(), vpAfma6::get_eJe(), vpBiclops::get_eJe(), vpPtu46::get_fJe(), vpAfma4::get_fJe(), vpAfma6::get_fJe(), vpBiclops::get_fJe(), vpAfma4::get_fJe_inverse(), vpViper::get_fJw(), vpCameraParameters::get_K(), vpCameraParameters::get_K_inverse(), vpRotationMatrix::init(), vpProjectionDisplay::init(), vpVelocityTwistMatrix::init(), vpForceTwistMatrix::init(), vpKalmanFilter::init(), vpHomogeneousMatrix::init(), vpMatrix::init(), vpMbtDistanceCylinder::initInteractionMatrixError(), vpMatrix::insert(), vpFeatureEllipse::interaction(), vpFeatureVanishingPoint::interaction(), vpFeatureLuminance::interaction(), vpFeatureSegment::interaction(), vpGenericFeature::interaction(), vpFeatureDepth::interaction(), vpFeaturePoint::interaction(), vpFeatureLine::interaction(), vpFeaturePoint3D::interaction(), vpFeaturePointPolar::interaction(), vpFeatureThetaU::interaction(), vpFeatureTranslation::interaction(), vpMatrix::juxtaposeMatrices(), vpMatrix::kernel(), vpMatrix::loadMatrix(), vpMatrix::mult2Matrices(), vpMatrix::negateMatrix(), vpMatrix::operator*(), vpMatrix::operator/(), vpMatrix::operator=(), vpPose::poseDementhonNonPlan(), vpPose::poseDementhonPlan(), vpPose::poseVirtualVSrobust(), vpMatrix::pseudoInverse(), vpIoTools::readConfigVar(), vpRowVector::reshape(), vpColVector::reshape(), vpRowVector::resize(), vpColVector::resize(), vpServo::secondaryTask(), vpColVector::skew(), vpMatrix::skew(), vpMatrix::stackMatrices(), vpMatrix::sub2Matrices(), vpMatrix::svd(), vpMatrix::t(), vpMatrix::transpose(), and vpMatrix::vpMatrix().
|
inherited |
Row extraction.
Return the ith rows of the matrix.
Definition at line 2225 of file vpMatrix.cpp.
References vpMatrix::getCols().
Referenced by vpMatrix::kernel(), vpMatrix::pseudoInverse(), and vpMatrix::transpose().
| void vpHomography::save | ( | std::ofstream & | f | ) | const |
Save an homography in a file.
Definition at line 298 of file vpHomography.cpp.
References vpException::ioError, and vpERROR_TRACE.
|
staticinherited |
Save a matrix to a file.
| filename | : Absolute file name. |
| M | : Matrix to be saved. |
| binary | : If true the matrix is saved in a binary file, else a text file. |
| Header | : Optional line that will be saved at the beginning of the file. |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 3440 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
Referenced by vpDot2::defineDots(), and vpMatrix::saveMatrix().
|
inlinestaticinherited |
Save a matrix to a file.
| filename | : absolute file name |
| M | : matrix to be saved |
| binary | :If true the matrix is save in a binary file, else a text file. |
| Header | : optional line that will be saved at the beginning of the file |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 201 of file vpMatrix.h.
References vpMatrix::saveMatrix().
|
inherited |
By default set the matrix to identity. More generally set M[i][i] = val.
Definition at line 1110 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
Referenced by vpServo::computeControlLaw(), computeTransformation(), vpMatrix::expm(), HartleyDenormalization(), HLM(), vpFeatureThetaU::interaction(), vpMeLine::leastSquare(), vpPose::poseFromRectangle(), and vpServo::secondaryTask().
|
inherited |
Solve a linear system 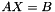 using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| b | : Vector 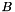 . . |
| x | : Vector 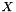 . . |
Here an example:
Definition at line 1573 of file vpMatrix.cpp.
References vpMatrix::pseudoInverse().
Referenced by vpMatrix::solveBySVD().
|
inherited |
Solve a linear system 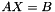 using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| B | : Vector 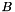 . . |
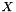 .
.Here an example:
Definition at line 1628 of file vpMatrix.cpp.
References vpMatrix::colNum, and vpMatrix::solveBySVD().
|
inherited |
Stacks columns of a matrix in a vector.
| out | : a vpColVector. |
Definition at line 1373 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpColVector::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
|
inherited |
Stacks columns of a matrix in a vector.
Definition at line 1397 of file vpMatrix.cpp.
References vpMatrix::colNum, and vpMatrix::rowNum.
Stack two Matrices C = [ A B ]^T.
Stack matrices. "Stack" two matrices C = [ A B ]^T.
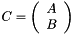
| A | : Upper matrix. |
| B | : Lower matrix. |
Definition at line 2263 of file vpMatrix.cpp.
References vpCERROR.
Referenced by vpCalibration::calibrationTsai(), computeDisplacement(), computeRotation(), vpMbEdgeKltTracker::computeVVS(), vpFeatureSegment::error(), vpFeatureEllipse::error(), vpFeatureVanishingPoint::error(), vpFeatureMomentAlpha::error(), vpGenericFeature::error(), vpFeaturePoint::error(), vpFeatureLine::error(), vpFeaturePoint3D::error(), vpFeaturePointPolar::error(), vpFeatureThetaU::error(), vpFeatureTranslation::error(), vpBasicFeature::get_s(), vpFeatureEllipse::interaction(), vpFeatureVanishingPoint::interaction(), vpFeatureSegment::interaction(), vpFeatureMoment::interaction(), vpGenericFeature::interaction(), vpFeaturePoint::interaction(), vpFeatureLine::interaction(), vpFeaturePoint3D::interaction(), vpFeaturePointPolar::interaction(), vpFeatureThetaU::interaction(), vpFeatureTranslation::interaction(), and vpMatrix::stackMatrices().
Stack two Matrices C = [ A B ]^T.
stackMatrices. "stack" two matrices C = [ A B ]^T
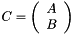
| A | : Upper matrix. |
| B | : Lower matrix. |
| C | : Stacked matrix C = [ A B ]^T |
Definition at line 2292 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
|
inherited |
Stack A at the end of the current matrix, or copy if the matrix has no dimensions : this = [ this A ]^T
Here an example for a robot velocity log :
Definition at line 2920 of file vpMatrix.cpp.
References vpMatrix::rowNum, and vpMatrix::stackMatrices().
|
inherited |
Stacks rows of a matrix in a vector
| out | : a vpRowVector. |
Definition at line 1408 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrix::dsize, vpRowVector::resize(), vpMatrix::rowNum, vpCERROR, and vpERROR_TRACE.
|
inherited |
Stacks rows of a matrix in a vector.
Definition at line 1430 of file vpMatrix.cpp.
References vpMatrix::colNum, and vpMatrix::rowNum.
|
staticinherited |
Operation C = A - B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 562 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator-().
|
inherited |
return sum of the Aij^2 (for all i, for all j)
Definition at line 760 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
Referenced by vpPose::calculArbreDementhon(), vpCalibration::calibrationTsai(), computeDisplacement(), computeResidual(), computeRotation(), vpPose::coplanar(), vpFeatureDepth::error(), vpFeatureThetaU::error(), vpFeatureTranslation::error(), vpMbTracker::extractCylinders(), vpFeatureThetaU::interaction(), vpMatrix::kernel(), vpRowVector::normalize(), vpColVector::normalize(), vpPose::poseDementhonNonPlan(), vpPose::poseDementhonPlan(), vpPose::poseFromRectangle(), vpPose::poseLagrangeNonPlan(), vpPose::poseLagrangePlan(), vpPose::poseVirtualVS(), vpPose::poseVirtualVSrobust(), vpMatrix::pseudoInverse(), vpServoData::save(), vpSimulatorAfma6::setPosition(), and vpSimulatorViper850::setPosition().
|
inherited |
Singular value decomposition (SVD).
![\[ M = U \Sigma V^{\top} \]](form_182.png)
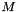 to decompose. You should make a COPY of that matrix if needed not to CHANGE.
to decompose. You should make a COPY of that matrix if needed not to CHANGE.| w | : Vector of singular values. 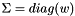 . . |
| v | : Matrix 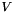 . . |
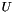 .
.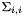 are ordered in decreasing fashion in w. This is not the case, if the GSL is not detected by ViSP.
are ordered in decreasing fashion in w. This is not the case, if the GSL is not detected by ViSP.Here an example of SVD decomposition of a non square Matrix M.
Definition at line 1702 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpColVector::resize(), and vpMatrix::resize().
Referenced by computeDisplacement(), DLT(), vpMatrix::kernel(), vpPose::poseDementhonPlan(), and vpMatrix::pseudoInverse().
|
inherited |
Compute and return the transpose of the matrix.
Definition at line 1176 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpCERROR, and vpERROR_TRACE.
Referenced by vpVelocityTwistMatrix::buildFrom(), vpForceTwistMatrix::buildFrom(), vpHomogeneousMatrix::buildFrom(), vpCalibration::calibrationTsai(), vpServo::computeControlLaw(), vpMatrix::computeCovarianceMatrix(), computeRotation(), vpMatrix::eigenValues(), vpKalmanFilter::filtering(), vpPose::poseDementhonNonPlan(), vpPose::poseDementhonPlan(), vpKalmanFilter::prediction(), vpMatrix::pseudoInverse(), and vpMatrix::resize().
|
inherited |
Compute and return the transpose of the matrix.
Definition at line 1206 of file vpMatrix.cpp.
|
inherited |
Compute At the transpose of the matrix.
| At | : Resulting transpose matrix. |
Definition at line 1218 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::row(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
Multiplication by a scalar Cij = x*Bij.
Definition at line 886 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrix::resize(), and vpERROR_TRACE.
|
related |
Compute the skew symmetric matrix 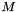 of translation vector
of translation vector 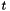 (matrice de pre-produit vectoriel).
(matrice de pre-produit vectoriel).
![\[ \mbox{if} \quad {\bf t} = \left( \begin{array}{c} t_x \\ t_y \\ t_z \end{array}\right), \quad \mbox{then} \qquad M = \left( \begin{array}{ccc} 0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0 \end{array}\right) \]](form_400.png)
| t | : Translation vector in input used to compute the skew symmetric matrix M. |
| M | : Skew symmetric matrix of translation vector 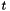 . . |
Definition at line 296 of file vpTranslationVector.cpp.
References vpMatrix::resize().
|
related |
This function performs generalized matrix multiplication: D = alpha*op(A)*op(B) + beta*op(C), where op(X) is X or X^T. Operation on A, B and C matrices is described by enumeration vpGEMMmethod.
For example, to compute alpha*A^T*B^T+beta*C we need to call :
If C is not used, vpGEMM must be called using an empty matrix null :
| vpMatrixException::incorrectMatrixSizeError | if the sizes of the matrices do not allow the operations. |
| A | : a Matrix |
| B | : a Matrix |
| alpha | : a scalar |
| C | : a Matrix |
| beta | : a scalar |
| D | : a Matrix |
| ops | : a scalar describing operation applied on the matrices |
Definition at line 331 of file vpGEMM.h.
References vpMatrixException::incorrectMatrixSizeError, and vpERROR_TRACE.
|
related |
Enumeration of the operations applied on matrices in vpGEMM function.
Operations are :
|
protectedinherited |
number of columns
Definition at line 112 of file vpMatrix.h.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::AtA(), vpMatrix::eigenValues(), vpMatrix::expm(), vpMatrix::eye(), vpMatrix::infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpMatrix::insert(), vpMatrix::inverseByCholesky(), vpMatrix::inverseByLU(), vpMatrix::inverseByQR(), vpMatrix::inverseByQRLapack(), vpMatrix::kron(), vpMatrix::mult2Matrices(), vpMatrix::multMatrixVector(), vpMatrix::negateMatrix(), vpRowVector::operator*(), vpMatrix::operator*(), vpMatrix::operator*=(), vpMatrix::operator+=(), vpMatrix::operator-=(), vpMatrix::operator/(), vpMatrix::operator/=(), vpColVector::operator<<(), vpMatrix::operator<<(), vpSubRowVector::operator=(), vpRowVector::operator=(), vpSubMatrix::operator=(), vpMatrix::operator=(), vpMatrix::resize(), vpMatrix::setIdentity(), vpMatrix::solveBySVD(), vpMatrix::stackColumns(), vpMatrix::stackRows(), vpMatrix::sub2Matrices(), vpMatrix::sumSquare(), vpRowVector::t(), vpMatrix::t(), vpMatrix::transpose(), vpMatrix::vpMatrix(), vpSubColVector::vpSubColVector(), vpSubMatrix::vpSubMatrix(), and vpSubRowVector::vpSubRowVector().
|
inherited |
address of the first element of the data array
Definition at line 116 of file vpMatrix.h.
Referenced by vpMatrix::AtA(), vpSubColVector::checkParentStatus(), vpSubRowVector::checkParentStatus(), vpSubMatrix::checkParentStatus(), vpPose::computeResidual(), computeResidual(), vpPose::computeTransformation(), computeTransformation(), vpColVector::dotProd(), vpMatrix::eigenValues(), vpMatrix::euclideanNorm(), vpRobotViper650::getForceTorque(), vpRobotViper850::getForceTorque(), vpMatrix::getMaxValue(), vpMatrix::getMinValue(), vpRobotViper650::getPosition(), vpRobotViper850::getPosition(), vpRobotViper850::getVelocity(), vpRobotViper650::getVelocity(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpRobotViper650::init(), vpRobotViper850::init(), vpMatrix::inverseByCholeskyLapack(), vpMatrix::inverseByQRLapack(), vpColVector::invSort(), vpMatrix::kill(), vpColVector::mean(), vpColVector::median(), vpRowVector::operator*(), vpColVector::operator*(), vpTranslationVector::operator*(), operator*(), vpColVector::operator+(), vpTranslationVector::operator-(), vpColVector::operator-(), operator/(), vpSubColVector::operator=(), vpSubRowVector::operator=(), vpRowVector::operator=(), vpColVector::operator=(), vpTranslationVector::operator=(), vpMatrix::operator=(), vpRowVector::operator[](), vpColVector::operator[](), vpPose::ransac(), ransac(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::resize(), vpRobotAfma4::setPosition(), vpRobotViper650::setPosition(), vpRobotViper850::setPosition(), vpRobotAfma4::setVelocity(), vpRobotAfma6::setVelocity(), vpRobotViper650::setVelocity(), vpRobotViper850::setVelocity(), vpColVector::sort(), vpMatrix::stackColumns(), vpMatrix::stackRows(), vpRowVector::t(), vpColVector::t(), vpColVector::vpColVector(), vpMatrix::vpMatrix(), vpSubColVector::vpSubColVector(), vpSubMatrix::vpSubMatrix(), vpSubRowVector::vpSubRowVector(), vpSubColVector::~vpSubColVector(), vpSubMatrix::~vpSubMatrix(), and vpSubRowVector::~vpSubRowVector().
|
protectedinherited |
Current size (rowNum * colNum)
Definition at line 122 of file vpMatrix.h.
Referenced by vpMatrix::euclideanNorm(), vpMatrix::getMaxValue(), vpMatrix::getMinValue(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpTranslationVector::operator*(), vpTranslationVector::operator-(), vpMatrix::operator=(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::resize(), vpMatrix::stackRows(), vpSubColVector::vpSubColVector(), vpSubMatrix::vpSubMatrix(), and vpSubRowVector::vpSubRowVector().
|
protectedinherited |
number of rows
Definition at line 110 of file vpMatrix.h.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::AtA(), vpColVector::deg2rad(), vpMatrix::eigenValues(), vpMatrix::expm(), vpMatrix::eye(), vpMatrix::infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpMatrix::insert(), vpMatrix::inverseByCholesky(), vpMatrix::inverseByCholeskyLapack(), vpMatrix::inverseByLU(), vpMatrix::inverseByQR(), vpMatrix::inverseByQRLapack(), vpMatrix::kron(), vpMatrix::mult2Matrices(), vpMatrix::multMatrixVector(), vpMatrix::negateMatrix(), vpColVector::operator*(), vpHomogeneousMatrix::operator*(), vpMatrix::operator*(), vpMatrix::operator*=(), vpColVector::operator+(), vpMatrix::operator+=(), vpColVector::operator-(), vpMatrix::operator-=(), vpMatrix::operator/(), vpMatrix::operator/=(), vpColVector::operator<<(), vpMatrix::operator<<(), vpSubColVector::operator=(), vpSubRowVector::operator=(), vpRowVector::operator=(), vpSubMatrix::operator=(), vpColVector::operator=(), vpTranslationVector::operator=(), vpMatrix::operator=(), vpColVector::rad2deg(), vpMatrix::resize(), vpMatrix::setIdentity(), vpColVector::stack(), vpMatrix::stackColumns(), vpMatrix::stackMatrices(), vpMatrix::stackRows(), vpMatrix::sub2Matrices(), vpMatrix::sumSquare(), vpColVector::t(), vpMatrix::t(), vpMatrix::transpose(), vpMatrix::vpMatrix(), vpSubColVector::vpSubColVector(), vpSubMatrix::vpSubMatrix(), and vpSubRowVector::vpSubRowVector().
|
protectedinherited |
address of the first element of each rows
Definition at line 119 of file vpMatrix.h.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpMatrix::kill(), vpMatrix::mult2Matrices(), vpMatrix::multMatrixVector(), vpMatrix::negateMatrix(), vpRotationMatrix::operator*(), vpVelocityTwistMatrix::operator*(), vpForceTwistMatrix::operator*(), vpHomogeneousMatrix::operator*(), vpMatrix::operator*(), vpMatrix::operator*=(), vpMatrix::operator+=(), vpMatrix::operator-=(), vpMatrix::operator/(), vpMatrix::operator/=(), vpColVector::operator<<(), vpMatrix::operator<<(), vpRowVector::operator=(), vpSubMatrix::operator=(), vpRotationMatrix::operator=(), vpVelocityTwistMatrix::operator=(), vpForceTwistMatrix::operator=(), vpHomogeneousMatrix::operator=(), vpMatrix::operator=(), vpMatrix::resize(), vpMatrix::stackColumns(), vpMatrix::sub2Matrices(), vpMatrix::sumSquare(), vpMatrix::transpose(), vpSubColVector::vpSubColVector(), vpSubMatrix::vpSubMatrix(), and vpSubRowVector::vpSubRowVector().
|
protectedinherited |
Total row space.
Definition at line 124 of file vpMatrix.h.
Referenced by vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpMatrix::resize(), vpSubColVector::vpSubColVector(), vpSubMatrix::vpSubMatrix(), and vpSubRowVector::vpSubRowVector().