 |
Visual Servoing Platform
version 3.6.1 under development (2024-04-27)
|
 |
Visual Servoing Platform
version 3.6.1 under development (2024-04-27)
|
#include <visp3/core/vpMatrix.h>
 Inheritance diagram for vpMatrix:
Inheritance diagram for vpMatrix:Public Types | |
| enum | vpDetMethod { LU_DECOMPOSITION } |
Public Member Functions | |
| vpMatrix () | |
| vpMatrix (unsigned int r, unsigned int c) | |
| vpMatrix (unsigned int r, unsigned int c, double val) | |
| vpMatrix (const vpMatrix &M, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) | |
| vpMatrix (const vpArray2D< double > &A) | |
| vpMatrix (const vpMatrix &A) | |
| vpMatrix (vpMatrix &&A) | |
| vpMatrix (const std::initializer_list< double > &list) | |
| vpMatrix (unsigned int nrows, unsigned int ncols, const std::initializer_list< double > &list) | |
| vpMatrix (const std::initializer_list< std::initializer_list< double > > &lists) | |
| void | clear () |
Setting a diagonal matrix <br> | |
| void | diag (const double &val=1.0) |
| void | diag (const vpColVector &A) |
| void | eye () |
| void | eye (unsigned int n) |
| void | eye (unsigned int m, unsigned int n) |
Assignment operators | |
| vpMatrix & | operator<< (double *) |
| vpMatrix & | operator<< (double val) |
| vpMatrix & | operator, (double val) |
| vpMatrix & | operator= (const vpArray2D< double > &A) |
| vpMatrix & | operator= (const vpMatrix &A) |
| vpMatrix & | operator= (vpMatrix &&A) |
| vpMatrix & | operator= (const std::initializer_list< double > &list) |
| vpMatrix & | operator= (const std::initializer_list< std::initializer_list< double > > &lists) |
| vpMatrix & | operator= (double x) |
Stacking <br> | |
| void | stack (const vpMatrix &A) |
| void | stack (const vpRowVector &r) |
| void | stack (const vpColVector &c) |
| void | stackColumns (vpColVector &out) |
| vpColVector | stackColumns () |
| void | stackRows (vpRowVector &out) |
| vpRowVector | stackRows () |
Matrix insertion | |
| void | insert (const vpMatrix &A, unsigned int r, unsigned int c) |
Columns, rows, sub-matrices extraction | |
| vpMatrix | extract (unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) const |
| vpColVector | getCol (unsigned int j) const |
| vpColVector | getCol (unsigned int j, unsigned int i_begin, unsigned int size) const |
| vpRowVector | getRow (unsigned int i) const |
| vpRowVector | getRow (unsigned int i, unsigned int j_begin, unsigned int size) const |
| vpColVector | getDiag () const |
| void | init (const vpMatrix &M, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) |
Matrix operations <br> | |
| double | det (vpDetMethod method=LU_DECOMPOSITION) const |
| double | detByLU () const |
| double | detByLUEigen3 () const |
| double | detByLULapack () const |
| double | detByLUOpenCV () const |
| vpMatrix | expm () const |
| vpMatrix & | operator+= (const vpMatrix &B) |
| vpMatrix & | operator-= (const vpMatrix &B) |
| vpMatrix | operator* (const vpMatrix &B) const |
| vpMatrix | operator* (const vpRotationMatrix &R) const |
| vpMatrix | operator* (const vpHomogeneousMatrix &R) const |
| vpMatrix | operator* (const vpVelocityTwistMatrix &V) const |
| vpMatrix | operator* (const vpForceTwistMatrix &V) const |
| vpTranslationVector | operator* (const vpTranslationVector &tv) const |
| vpColVector | operator* (const vpColVector &v) const |
| vpMatrix | operator+ (const vpMatrix &B) const |
| vpMatrix | operator- (const vpMatrix &B) const |
| vpMatrix | operator- () const |
| vpMatrix & | operator+= (double x) |
| vpMatrix & | operator-= (double x) |
| vpMatrix & | operator*= (double x) |
| vpMatrix & | operator/= (double x) |
| vpMatrix | operator* (double x) const |
| vpMatrix | operator/ (double x) const |
| double | sum () const |
| double | sumSquare () const |
Hadamard product <br> | |
| vpMatrix | hadamard (const vpMatrix &m) const |
Kronecker product <br> | |
| void | kron (const vpMatrix &m1, vpMatrix &out) const |
| vpMatrix | kron (const vpMatrix &m1) const |
Transpose <br> | |
| vpMatrix | t () const |
| vpMatrix | transpose () const |
| void | transpose (vpMatrix &At) const |
| vpMatrix | AAt () const |
| void | AAt (vpMatrix &B) const |
| vpMatrix | AtA () const |
| void | AtA (vpMatrix &B) const |
Matrix inversion <br> | |
| vpMatrix | inverseByLU () const |
| vpMatrix | inverseByLUEigen3 () const |
| vpMatrix | inverseByLULapack () const |
| vpMatrix | inverseByLUOpenCV () const |
| vpMatrix | inverseByCholesky () const |
| vpMatrix | inverseByCholeskyLapack () const |
| vpMatrix | inverseByCholeskyOpenCV () const |
| vpMatrix | inverseByQR () const |
| vpMatrix | inverseByQRLapack () const |
| vpMatrix | inverseTriangular (bool upper=true) const |
| vpMatrix | pseudoInverse (double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverse (int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt) const |
| int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseLapack (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseLapack (int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseLapack (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseEigen3 (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseEigen3 (int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseEigen3 (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseOpenCV (double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
| vpMatrix | pseudoInverseOpenCV (int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, int rank_in) const |
| int | pseudoInverseOpenCV (vpMatrix &Ap, vpColVector &sv, int rank_in, vpMatrix &imA, vpMatrix &imAt, vpMatrix &kerAt) const |
SVD decomposition <br> | |
| double | cond (double svThreshold=1e-6) const |
| unsigned int | kernel (vpMatrix &kerAt, double svThreshold=1e-6) const |
| unsigned int | nullSpace (vpMatrix &kerA, double svThreshold=1e-6) const |
| unsigned int | nullSpace (vpMatrix &kerA, int dim) const |
| void | solveBySVD (const vpColVector &B, vpColVector &x) const |
| vpColVector | solveBySVD (const vpColVector &B) const |
| void | svd (vpColVector &w, vpMatrix &V) |
| void | svdEigen3 (vpColVector &w, vpMatrix &V) |
| void | svdLapack (vpColVector &w, vpMatrix &V) |
| void | svdOpenCV (vpColVector &w, vpMatrix &V) |
QR decomposition <br> | |
| unsigned int | qr (vpMatrix &Q, vpMatrix &R, bool full=false, bool squareR=false, double tol=1e-6) const |
| unsigned int | qrPivot (vpMatrix &Q, vpMatrix &R, vpMatrix &P, bool full=false, bool squareR=false, double tol=1e-6) const |
| void | solveByQR (const vpColVector &b, vpColVector &x) const |
| vpColVector | solveByQR (const vpColVector &b) const |
Eigen values <br> | |
| vpColVector | eigenValues () const |
| void | eigenValues (vpColVector &evalue, vpMatrix &evector) const |
Norms <br> | |
| double | frobeniusNorm () const |
| double | inducedL2Norm () const |
| double | infinityNorm () const |
Printing <br> | |
| std::ostream & | cppPrint (std::ostream &os, const std::string &matrixName="A", bool octet=false) const |
| std::ostream & | csvPrint (std::ostream &os) const |
| std::ostream & | maplePrint (std::ostream &os) const |
| std::ostream & | matlabPrint (std::ostream &os) const |
| int | print (std::ostream &s, unsigned int length, const std::string &intro="") const |
| void | printSize () const |
Inherited functionalities from vpArray2D | |
| unsigned int | getCols () const |
| double | getMaxValue () const |
| double | getMinValue () const |
| unsigned int | getRows () const |
| unsigned int | size () const |
| void | resize (unsigned int nrows, unsigned int ncols, bool flagNullify=true, bool recopy_=true) |
| void | reshape (unsigned int nrows, unsigned int ncols) |
| void | insert (const vpArray2D< double > &A, unsigned int r, unsigned int c) |
| bool | operator== (const vpArray2D< double > &A) const |
| bool | operator!= (const vpArray2D< double > &A) const |
| double * | operator[] (unsigned int i) |
| double * | operator[] (unsigned int i) const |
| vpArray2D< double > | hadamard (const vpArray2D< double > &m) const |
Static Public Member Functions | |
Linear algebra optimization <br> | |
| static unsigned int | getLapackMatrixMinSize () |
| static void | setLapackMatrixMinSize (unsigned int min_size) |
Setting a diagonal matrix with Static Public Member Functions <br> | |
| static void | createDiagonalMatrix (const vpColVector &A, vpMatrix &DA) |
Matrix insertion with Static Public Member Functions <br> | |
| static vpMatrix | insert (const vpMatrix &A, const vpMatrix &B, unsigned int r, unsigned int c) |
| static void | insert (const vpMatrix &A, const vpMatrix &B, vpMatrix &C, unsigned int r, unsigned int c) |
Stacking with Static Public Member Functions <br> | |
| static vpMatrix | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B) |
| static void | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static vpMatrix | stack (const vpMatrix &A, const vpMatrix &B) |
| static vpMatrix | stack (const vpMatrix &A, const vpRowVector &r) |
| static vpMatrix | stack (const vpMatrix &A, const vpColVector &c) |
| static void | stack (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | stack (const vpMatrix &A, const vpRowVector &r, vpMatrix &C) |
| static void | stack (const vpMatrix &A, const vpColVector &c, vpMatrix &C) |
Matrix operations with Static Public Member Functions <br> | |
| static void | add2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | add2Matrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
| static void | add2WeightedMatrices (const vpMatrix &A, const double &wA, const vpMatrix &B, const double &wB, vpMatrix &C) |
| static void | computeHLM (const vpMatrix &H, const double &alpha, vpMatrix &HLM) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpRotationMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpHomogeneousMatrix &C) |
| static void | mult2Matrices (const vpMatrix &A, const vpColVector &B, vpColVector &C) |
| static void | multMatrixVector (const vpMatrix &A, const vpColVector &v, vpColVector &w) |
| static void | negateMatrix (const vpMatrix &A, vpMatrix &C) |
| static void | sub2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | sub2Matrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
Kronecker product with Static Public Member Functions <br> | |
| static void | kron (const vpMatrix &m1, const vpMatrix &m2, vpMatrix &out) |
| static vpMatrix | kron (const vpMatrix &m1, const vpMatrix &m2) |
Covariance computation with Static Public Member Functions <br> | |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b) |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b, const vpMatrix &w) |
| static vpMatrix | computeCovarianceMatrixVVS (const vpHomogeneousMatrix &cMo, const vpColVector &deltaS, const vpMatrix &Ls, const vpMatrix &W) |
| static vpMatrix | computeCovarianceMatrixVVS (const vpHomogeneousMatrix &cMo, const vpColVector &deltaS, const vpMatrix &Ls) |
Public Attributes | |
| double * | data |
Protected Attributes | |
| unsigned int | rowNum |
| unsigned int | colNum |
| double ** | rowPtrs |
| unsigned int | dsize |
Related Functions | |
(Note that these are not member functions.) | |
| vpMatrix | operator* (const double &x, const vpMatrix &B) |
| void | insert (const vpMatrix &A, const vpMatrix &B, vpMatrix &C, unsigned int r, unsigned int c) |
| enum | vpGEMMmethod |
| bool | operator== (const vpArray2D< double > &A) const |
| bool | operator== (const vpArray2D< float > &A) const |
| bool | operator!= (const vpArray2D< double > &A) const |
| void | vpGEMM (const vpArray2D< double > &A, const vpArray2D< double > &B, const double &alpha, const vpArray2D< double > &C, const double &beta, vpArray2D< double > &D, const unsigned int &ops=0) |
Deprecated functions | |
| vp_deprecated void | init () |
| vp_deprecated void | stackMatrices (const vpMatrix &A) |
| vp_deprecated void | setIdentity (const double &val=1.0) |
| vp_deprecated vpRowVector | row (unsigned int i) |
| vp_deprecated vpColVector | column (unsigned int j) |
| static vp_deprecated vpMatrix | stackMatrices (const vpMatrix &A, const vpMatrix &B) |
| static vp_deprecated void | stackMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static vp_deprecated vpMatrix | stackMatrices (const vpMatrix &A, const vpRowVector &B) |
| static vp_deprecated void | stackMatrices (const vpMatrix &A, const vpRowVector &B, vpMatrix &C) |
| static vp_deprecated vpMatrix | stackMatrices (const vpColVector &A, const vpColVector &B) |
| static vp_deprecated void | stackMatrices (const vpColVector &A, const vpColVector &B, vpColVector &C) |
Matrix I/O with Static Public Member Functions <br> | |
| vp_deprecated double | euclideanNorm () const |
| static bool | loadMatrix (const std::string &filename, vpArray2D< double > &M, bool binary=false, char *header=nullptr) |
| static bool | loadMatrixYAML (const std::string &filename, vpArray2D< double > &M, char *header=nullptr) |
| static bool | saveMatrix (const std::string &filename, const vpArray2D< double > &M, bool binary=false, const char *header="") |
| static bool | saveMatrixYAML (const std::string &filename, const vpArray2D< double > &M, const char *header="") |
Inherited I/O from vpArray2D with Static Public Member Functions | |
| vpArray2D< double > | insert (const vpArray2D< double > &A, const vpArray2D< double > &B, unsigned int r, unsigned int c) |
| static bool | load (const std::string &filename, vpArray2D< double > &A, bool binary=false, char *header=nullptr) |
| static bool | loadYAML (const std::string &filename, vpArray2D< double > &A, char *header=nullptr) |
| static bool | save (const std::string &filename, const vpArray2D< double > &A, bool binary=false, const char *header="") |
| static bool | saveYAML (const std::string &filename, const vpArray2D< double > &A, const char *header="") |
| static vpArray2D< double > | conv2 (const vpArray2D< double > &M, const vpArray2D< double > &kernel, const std::string &mode) |
| static void | conv2 (const vpArray2D< double > &M, const vpArray2D< double > &kernel, vpArray2D< double > &res, const std::string &mode) |
| static void | insert (const vpArray2D< double > &A, const vpArray2D< double > &B, vpArray2D< double > &C, unsigned int r, unsigned int c) |
Implementation of a matrix and operations on matrices.
This class needs one of the following third-party to compute matrix inverse, pseudo-inverse, singular value decomposition, determinant:
vpMatrix class provides a data structure for the matrices as well as a set of operations on these matrices.
The vpMatrix class is derived from vpArray2D<double>.
The code below shows how to create a 2-by-3 matrix of doubles, set the element values and access them:
Once build, this previous code produces the following output:
If ViSP is build with c++11 enabled, you can do the same using:
You can also create and initialize a matrix this way:
The Matrix could also be initialized using operator=(const std::initializer_list< std::initializer_list< double > > &)
Definition at line 145 of file vpMatrix.h.
Method used to compute the determinant of a square matrix.
| Enumerator | |
|---|---|
| LU_DECOMPOSITION | LU decomposition method. |
Definition at line 152 of file vpMatrix.h.
|
inline |
Basic constructor of a matrix of double. Number of columns and rows are zero.
Definition at line 162 of file vpMatrix.h.
Referenced by insert().
|
inline |
Constructor that initialize a matrix of double with 0.
| r | : Matrix number of rows. |
| c | : Matrix number of columns. |
Definition at line 170 of file vpMatrix.h.
|
inline |
Constructor that initialize a matrix of double with val.
| r | : Matrix number of rows. |
| c | : Matrix number of columns. |
| val | : Each element of the matrix is set to val. |
Definition at line 179 of file vpMatrix.h.
| vpMatrix::vpMatrix | ( | const vpMatrix & | M, |
| unsigned int | r, | ||
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) |
Construct a matrix as a sub-matrix of the input matrix M.
Definition at line 190 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, init(), and vpArray2D< Type >::rowNum.
|
inline |
Create a matrix from a 2D array that could be one of the following container that inherit from vpArray2D such as vpMatrix, vpRotationMatrix, vpHomogeneousMatrix, vpPoseVector, vpColVector, vpRowVector...
The following example shows how to create a matrix from an homogeneous matrix:
Definition at line 194 of file vpMatrix.h.
|
inline |
Definition at line 196 of file vpMatrix.h.
| vpMatrix::vpMatrix | ( | vpMatrix && | A | ) |
Definition at line 205 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< double >::dsize, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
|
explicit |
Construct a matrix from a list of double values.
| list | : List of double. |
The following code shows how to use this constructor to initialize a 2-by-3 matrix using reshape() function:
It produces the following output:
Definition at line 243 of file vpMatrix.cpp.
|
explicit |
Construct a matrix from a list of double values.
| ncols,nrows | : Matrix size. |
| list | : List of double. |
The following code shows how to use this constructor to initialize a 2-by-3 matrix:
It produces the following output:
Definition at line 267 of file vpMatrix.cpp.
|
explicit |
Construct a matrix from a list of double values.
| lists | : List of double. The following code shows how to use this constructor to initialize a 2-by-3 matrix function: #include <visp3/core/vpMatrix.h>
int main()
{
vpMatrix M( { {-1, -2, -3}, {4, 5.5, 6} } );
std::cout << "M:\n" << M << std::endl;
}
M:
-1 -2 -3
4 5.5 6
|
Definition at line 291 of file vpMatrix.cpp.
| vpMatrix vpMatrix::AAt | ( | ) | const |
Computes the ![]() operation
operation ![]()
Definition at line 517 of file vpMatrix.cpp.
Referenced by vpServo::computeControlLaw(), and vpServo::computeProjectionOperators().
| void vpMatrix::AAt | ( | vpMatrix & | B | ) | const |
Compute the AAt operation such as ![]() .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 537 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, vpArray2D< Type >::rowNum, and vpArray2D< double >::rowPtrs.
|
static |
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new vector won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1455 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1421 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator+().
|
static |
Operation C = A*wA + B*wB
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 1389 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
| vpMatrix vpMatrix::AtA | ( | ) | const |
Compute the AtA operation such as ![]()
Definition at line 645 of file vpMatrix.cpp.
Referenced by vpServo::computeProjectionOperators(), vpMbDepthDenseTracker::computeVVS(), vpMbDepthNormalTracker::computeVVS(), vpMbGenericTracker::computeVVS(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpTemplateTrackerWarpHomographySL3::findWarp(), and vpNurbs::globalCurveApprox().
| void vpMatrix::AtA | ( | vpMatrix & | B | ) | const |
Compute the AtA operation such as ![]() .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 593 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< Type >::rowNum.
|
inline |
Removes all elements from the matrix (which are destroyed), leaving the container with a size of 0.
Definition at line 209 of file vpMatrix.h.
| vpColVector vpMatrix::column | ( | unsigned int | j | ) |
should be replaced with:
| j | : Index of the column to extract noting that column index start at 1 to get the first column. |
Definition at line 6680 of file vpMatrix.cpp.
References vpArray2D< double >::getRows().
|
static |
Compute the covariance matrix of the parameters x from a least squares minimization defined as: Ax = b
| A | : Matrix A from Ax = b. |
| x | : Vector x from Ax = b corresponding to the parameters to estimate. |
| b | : Vector b from Ax = b. |
Definition at line 59 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), pseudoInverse(), and t().
Referenced by computeCovarianceMatrixVVS(), and vpPose::poseVirtualVSrobust().
|
static |
Compute the covariance matrix of the parameters x from a least squares minimization defined as: WAx = Wb
| A | : Matrix A from WAx = Wb. |
| x | : Vector x from WAx = Wb corresponding to the parameters to estimate. |
| b | : Vector b from WAx = Wb. |
| W | : Diagonal weigths matrix from WAx = Wb. |
Definition at line 92 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpArray2D< Type >::getCols(), pseudoInverse(), and t().
|
static |
Compute the covariance matrix of an image-based virtual visual servoing. This assumes the optimization has been done via v = Ls.pseudoInverse() * DeltaS.
| cMo | : Pose matrix that has been computed with the v. |
| deltaS | : Error vector used in v = Ls.pseudoInverse() * DeltaS |
| Ls | : interaction matrix used in v = Ls.pseudoInverse() * DeltaS |
Definition at line 127 of file vpMatrix_covariance.cpp.
References computeCovarianceMatrix(), and computeCovarianceMatrixVVS().
|
static |
Compute the covariance matrix of an image-based virtual visual servoing. This assumes the optimization has been done via v = (W * Ls).pseudoInverse() W * DeltaS.
| cMo | : Pose matrix that has been computed with the v. |
| deltaS | : Error vector used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
| Ls | : interaction matrix used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
| W | : Weight matrix used in v = (W * Ls).pseudoInverse() * W * DeltaS. |
Definition at line 152 of file vpMatrix_covariance.cpp.
References computeCovarianceMatrix().
Referenced by vpMbTracker::computeCovarianceMatrixVVS(), computeCovarianceMatrixVVS(), and vpPose::poseVirtualVS().
Compute ![]()
| H | : input Matrix 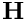 . This matrix should be square. . This matrix should be square. |
| alpha | : Scalar 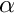 |
| HLM | : Resulting operation. |
Definition at line 6493 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
Referenced by vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerSSDESM::initCompInverse(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTrackerMIESM::initHessienDesired(), vpTemplateTrackerMIForwardAdditional::initHessienDesired(), vpTemplateTrackerMIForwardCompositional::initHessienDesired(), vpTemplateTrackerMIInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDESM::trackNoPyr(), vpTemplateTrackerSSDForwardAdditional::trackNoPyr(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), and vpTemplateTrackerMIInverseCompositional::trackNoPyr().
| double vpMatrix::cond | ( | double | svThreshold = 1e-6 | ) | const |
| svThreshold | Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Definition at line 6430 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), and svd().
Referenced by vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), and vpTemplateTrackerMIInverseCompositional::trackNoPyr().
|
staticinherited |
Perform a 2D convolution similar to Matlab conv2 function: ![]() .
.
| M | : First matrix. |
| kernel | : Second matrix. |
| mode | : Convolution mode: "full" (default), "same", "valid". |
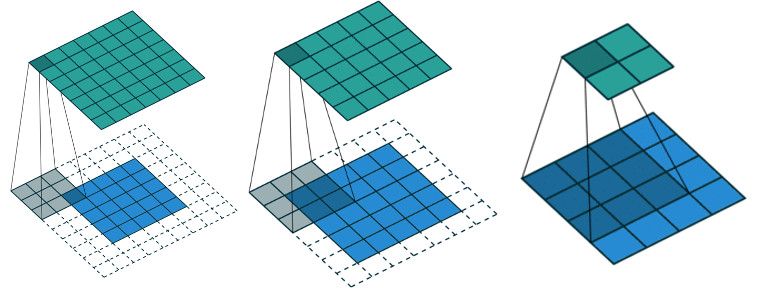
Definition at line 1029 of file vpArray2D.h.
|
staticinherited |
Perform a 2D convolution similar to Matlab conv2 function: ![]() .
.
| M | : First array. |
| kernel | : Second array. |
| res | : Result. |
| mode | : Convolution mode: "full" (default), "same", "valid". |

Definition at line 1043 of file vpArray2D.h.
| std::ostream & vpMatrix::cppPrint | ( | std::ostream & | os, |
| const std::string & | matrixName = "A", |
||
| bool | octet = false |
||
| ) | const |
Print to be used as part of a C++ code later.
| os | : the stream to be printed in. |
| matrixName | : name of the matrix, "A" by default. |
| octet | : if false, print using double, if true, print byte per byte each bytes of the double array. |
The following code shows how to use this function:
It produces the following output that could be copy/paste in a C++ code:
Definition at line 5642 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
|
static |
Create a diagonal matrix with the element of a vector ![]() .
.
| A | : Vector which element will be put in the diagonal. |
| DA | : Diagonal matrix DA[i][i] = A[i] |
Definition at line 929 of file vpMatrix.cpp.
References vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
| std::ostream & vpMatrix::csvPrint | ( | std::ostream & | os | ) | const |
Print/save a matrix in csv format.
The following code
produces log.csv file that contains:
Definition at line 5591 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
| double vpMatrix::det | ( | vpDetMethod | method = LU_DECOMPOSITION | ) | const |
Compute the determinant of a n-by-n matrix.
| method | : Method used to compute the determinant. Default LU decomposition method is faster than the method based on Gaussian elimination. |
Definition at line 6275 of file vpMatrix.cpp.
References detByLU(), and LU_DECOMPOSITION.
Referenced by vpHomogeneousMatrix::compute3d3dTransformation(), detByLULapack(), detByLUOpenCV(), vpTemplateTrackerTriangle::init(), inverseByLU(), and vpRotationMatrix::orthogonalize().
| double vpMatrix::detByLU | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition.
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default detByLULapack() with a Lapack built-in version.
Definition at line 224 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, detByLUEigen3(), detByLULapack(), detByLUOpenCV(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by det().
| double vpMatrix::detByLUEigen3 | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition with Eigen3 3rd party.
Definition at line 615 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< double >::rowNum.
Referenced by detByLU().
| double vpMatrix::detByLULapack | ( | ) | const |
Compute the determinant of a square matrix using the LU decomposition with Lapack 3rd party.
Definition at line 379 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, det(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by detByLU().
| double vpMatrix::detByLUOpenCV | ( | ) | const |
Compute the determinant of a n-by-n matrix using the LU decomposition with OpenCV 3rd party.
Definition at line 525 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, det(), vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by detByLU().
| void vpMatrix::diag | ( | const double & | val = 1.0 | ) |
Set the matrix as a diagonal matrix where each element on the diagonal is set to val. Elements that are not on the diagonal are set to 0.
| val | : Value to set. |
Matrix A is now equal to:
Definition at line 910 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by getDiag().
| void vpMatrix::diag | ( | const vpColVector & | A | ) |
Create a diagonal matrix with the element of a vector.
| A | : Vector which element will be put in the diagonal. |
Matrix A is now equal to:
Definition at line 869 of file vpMatrix.cpp.
References vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpColVector vpMatrix::eigenValues | ( | ) | const |
Compute the eigenvalues of a n-by-n real symmetric matrix using Lapack 3rd party.
| vpException::dimensionError | If the matrix is not square. |
| vpException::fatalError | If the matrix is not symmetric. |
| vpException::functionNotImplementedError | If the Lapack 3rd party is not detected. |
Here an example:
Definition at line 5836 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpException::functionNotImplementedError, vpColVector::resize(), vpArray2D< double >::rowNum, and t().
Referenced by vpQuadProg::fromCanonicalCost(), and vpMath::lineFitting().
| void vpMatrix::eigenValues | ( | vpColVector & | evalue, |
| vpMatrix & | evector | ||
| ) | const |
Compute the eigenvalues of a n-by-n real symmetric matrix using Lapack 3rd party.
| evalue | : Eigenvalues of the matrix, sorted in ascending order. |
| evector | : Corresponding eigenvectors of the matrix. |
| vpException::dimensionError | If the matrix is not square. |
| vpException::fatalError | If the matrix is not symmetric. |
| vpException::functionNotImplementedError | If Lapack 3rd party is not detected. |
Here an example:
Definition at line 5957 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpException::functionNotImplementedError, vpColVector::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and t().
| double vpMatrix::euclideanNorm | ( | ) | const |
Compute and return the Euclidean norm (also called Frobenius norm) ![]() .
.
Definition at line 6619 of file vpMatrix.cpp.
References frobeniusNorm().
| vpMatrix vpMatrix::expm | ( | ) | const |
Compute the exponential matrix of a square matrix.
Definition at line 6293 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, eye(), inverseByLU(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and sum().
Referenced by vpTemplateTrackerWarpHomographySL3::computeCoeff().
| vpMatrix vpMatrix::extract | ( | unsigned int | r, |
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) | const |
Extract a sub matrix from a matrix M.
| r | : row index in matrix M. |
| c | : column index in matrix M. |
| nrows | : Number of rows of the matrix that should be extracted. |
| ncols | : Number of columns of the matrix that should be extracted. |
The following code shows how to use this function:
It produces the following output:
Definition at line 404 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< Type >::resize().
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
| void vpMatrix::eye | ( | ) |
Set an m-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 448 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpServo::computeControlLaw(), vpMbDepthDenseTracker::computeVVS(), vpMbDepthNormalTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpMbEdgeKltTracker::computeVVS(), vpMbGenericTracker::computeVVS(), vpMbTracker::computeVVSPoseEstimation(), expm(), eye(), vpTemplateTrackerWarpHomographySL3::getdW0(), vpTemplateTrackerWarpHomographySL3::getdWdp0(), vpFeatureThetaU::interaction(), vpPose::poseFromRectangle(), vpRobotKinova::setCartVelocity(), vpServo::setServo(), vpLinProg::solveLP(), vpMbTracker::vpMbTracker(), and vpServo::vpServo().
| void vpMatrix::eye | ( | unsigned int | m, |
| unsigned int | n | ||
| ) |
Set an m-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 437 of file vpMatrix.cpp.
References eye(), and vpArray2D< double >::resize().
| void vpMatrix::eye | ( | unsigned int | n | ) |
Set an n-by-n matrix to identity with ones on the diagonal and zeros else where.
Definition at line 431 of file vpMatrix.cpp.
References eye().
| double vpMatrix::frobeniusNorm | ( | ) | const |
Compute and return the Frobenius norm (also called Euclidean norm) ![]() .
.
Definition at line 6514 of file vpMatrix.cpp.
References vpArray2D< double >::data, and vpArray2D< double >::dsize.
Referenced by euclideanNorm().
| vpColVector vpMatrix::getCol | ( | unsigned int | j | ) | const |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If j=0, the first column is extracted. |
The following example shows how to use this function:
It produces the following output :
Definition at line 4975 of file vpMatrix.cpp.
References vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpHomography::DLT(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), kernel(), vpPose::poseFromRectangle(), vpServo::secondaryTaskJointLimitAvoidance(), and vpLinProg::simplex().
| vpColVector vpMatrix::getCol | ( | unsigned int | j, |
| unsigned int | i_begin, | ||
| unsigned int | column_size | ||
| ) | const |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If col=0, the first column is extracted. |
| i_begin | : Index of the row that gives the location of the first element of the column vector to extract. |
| column_size | : Size of the column vector to extract. |
The following example shows how to use this function:
It produces the following output :
Definition at line 4923 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
|
inlineinherited |
Return the number of columns of the 2D array.
Definition at line 327 of file vpArray2D.h.
| vpColVector vpMatrix::getDiag | ( | ) | const |
Extract a diagonal vector from a matrix.
The following example shows how to use this function:
It produces the following output :
Definition at line 5102 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, diag(), and vpArray2D< double >::rowNum.
|
inlinestatic |
Return the minimum size of rows and columns required to enable Blas/Lapack usage on matrices and vectors.
To get more info see Tutorial: Basic linear algebra operations.
Definition at line 236 of file vpMatrix.h.
|
inherited |
Return the array max value.
Definition at line 329 of file vpArray2D.h.
|
inherited |
Return the array min value.
Definition at line 331 of file vpArray2D.h.
| vpRowVector vpMatrix::getRow | ( | unsigned int | i | ) | const |
Extract a row vector from a matrix.
| i | : Index of the row to extract. If i=0, the first row is extracted. |
The following example shows how to use this function:
It produces the following output:
Definition at line 5013 of file vpMatrix.cpp.
References vpArray2D< double >::colNum.
Referenced by vpLinProg::allClose(), vpLinProg::allLesser(), vpLinProg::solveLP(), and vpQuadProg::solveQPi().
| vpRowVector vpMatrix::getRow | ( | unsigned int | i, |
| unsigned int | j_begin, | ||
| unsigned int | row_size | ||
| ) | const |
Extract a row vector from a matrix.
| i | : Index of the row to extract. If i=0, the first row is extracted. |
| j_begin | : Index of the column that gives the location of the first element of the row vector to extract. |
| row_size | : Size of the row vector to extract. |
The following example shows how to use this function:
It produces the following output :
Definition at line 5054 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, and vpArray2D< double >::rowNum.
|
inlineinherited |
Return the number of rows of the 2D array.
Definition at line 337 of file vpArray2D.h.
Compute the Hadamard product (element wise matrix multiplication).
| m | : Second matrix; |
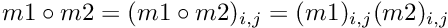
Definition at line 625 of file vpArray2D.h.
Compute the Hadamard product (element wise matrix multiplication).
| m | : Second matrix; |
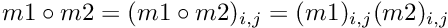
Definition at line 1863 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
| double vpMatrix::inducedL2Norm | ( | ) | const |
Compute and return the induced L2 norm ![]() which is equal to the maximum singular value of the matrix.
which is equal to the maximum singular value of the matrix.
Definition at line 6533 of file vpMatrix.cpp.
References vpArray2D< double >::dsize, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::size(), and svd().
| double vpMatrix::infinityNorm | ( | ) | const |
Compute and return the infinity norm ![]() with
with ![]() where
where ![]() is the matrix size.
is the matrix size.
Definition at line 6574 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by vpLinProg::colReduction(), and vpLinProg::rowReduction().
|
inline |
Definition at line 989 of file vpMatrix.h.
Referenced by vpMatrix(), and vpSubMatrix::vpSubMatrix().
| void vpMatrix::init | ( | const vpMatrix & | M, |
| unsigned int | r, | ||
| unsigned int | c, | ||
| unsigned int | nrows, | ||
| unsigned int | ncols | ||
| ) |
Initialize the matrix from a part of an input matrix M.
| M | : Input matrix used for initialization. |
| r | : row index in matrix M. |
| c | : column index in matrix M. |
| nrows | : Number of rows of the matrix that should be initialized. |
| ncols | : Number of columns of the matrix that should be initialized. |
The sub-matrix starting from M[r][c] element and ending on M[r+nrows-1][c+ncols-1] element is used to initialize the matrix.
The following code shows how to use this function:
It produces the following output:
Definition at line 340 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
|
inherited |
Insert array B in array A at the given position.
| A | : Main array. |
| B | : Array to insert. |
| r | : Index of the row where to add the array. |
| c | : Index of the column where to add the array. |
Definition at line 1057 of file vpArray2D.h.
|
inlineinherited |
Insert array A at the given position in the current array.
| A | : The array to insert. |
| r | : The index of the row to begin to insert data. |
| c | : The index of the column to begin to insert data. |
Definition at line 484 of file vpArray2D.h.
|
static |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| r | : Index of the row where to add the matrix. |
| c | : Index of the column where to add the matrix. |
Definition at line 5273 of file vpMatrix.cpp.
References vpArray2D< Type >::insert(), and vpMatrix().
|
static |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| C | : Result matrix. |
| r | : Index of the row where to insert matrix B. |
| c | : Index of the column where to insert matrix B. |
Definition at line 5295 of file vpMatrix.cpp.
References vpArray2D< Type >::insert().
| void vpMatrix::insert | ( | const vpMatrix & | A, |
| unsigned int | r, | ||
| unsigned int | c | ||
| ) |
Insert matrix A at the given position in the current matrix.
| A | : The matrix to insert. |
| r | : The index of the row to begin to insert data. |
| c | : The index of the column to begin to insert data. |
Definition at line 5781 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, and vpArray2D< Type >::size().
Referenced by vpMbDepthDenseTracker::computeVVSInteractionMatrixAndResidu(), vpMbDepthNormalTracker::computeVVSInteractionMatrixAndResidu(), vpMbGenericTracker::computeVVSInteractionMatrixAndResidu(), cond(), vpNurbs::curveKnotIns(), juxtaposeMatrices(), kernel(), nullSpace(), vpRobotKinova::setCartVelocity(), and stack().
| vpMatrix vpMatrix::inverseByCholesky | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition. The matrix must be real symmetric positive defined.
This function calls the first following function that is available:
If none of these 3rd parties is installed we use a Lapack built-in version.
Here an example:
Definition at line 112 of file vpMatrix_cholesky.cpp.
References vpException::fatalError, inverseByCholeskyLapack(), and inverseByCholeskyOpenCV().
| vpMatrix vpMatrix::inverseByCholeskyLapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition with Lapack 3rd party. The matrix must be real symmetric positive defined.
Here an example:
Definition at line 162 of file vpMatrix_cholesky.cpp.
References vpException::badValue, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::fatalError, vpArray2D< Type >::getCols(), vpArray2D< double >::getRows(), vpArray2D< Type >::getRows(), vpMatrixException::matrixError, and vpArray2D< double >::rowNum.
Referenced by inverseByCholesky().
| vpMatrix vpMatrix::inverseByCholeskyOpenCV | ( | ) | const |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition with OpenCV 3rd party. The matrix must be real symmetric positive defined.
Here an example:
Definition at line 255 of file vpMatrix_cholesky.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByCholesky().
| vpMatrix vpMatrix::inverseByLU | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition.
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default inverseByLULapack() with a Lapack built-in version.
Here an example:
Definition at line 127 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, det(), vpException::fatalError, inverseByLUEigen3(), inverseByLULapack(), inverseByLUOpenCV(), vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
Referenced by expm(), vpKalmanFilter::filtering(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerTriangle::init(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTrackerMIESM::initHessienDesired(), vpTemplateTrackerMIForwardAdditional::initHessienDesired(), vpTemplateTrackerMIForwardCompositional::initHessienDesired(), vpTemplateTrackerMIInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDForwardAdditional::trackNoPyr(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), vpTemplateTrackerMIESM::trackNoPyr(), vpTemplateTrackerMIForwardAdditional::trackNoPyr(), vpTemplateTrackerMIForwardCompositional::trackNoPyr(), vpTemplateTrackerMIInverseCompositional::trackNoPyr(), and vpImageTools::warpImage().
| vpMatrix vpMatrix::inverseByLUEigen3 | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with Eigen3 3rd party.
Here an example:
Definition at line 573 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByLULapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with Lapack 3rd party.
Here an example:
Definition at line 282 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByLUOpenCV | ( | ) | const |
Compute the inverse of a n-by-n matrix using the LU decomposition with OpenCV 3rd party.
Here an example:
Definition at line 484 of file vpMatrix_lu.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, and vpArray2D< double >::rowNum.
Referenced by inverseByLU().
| vpMatrix vpMatrix::inverseByQR | ( | ) | const |
Compute the inverse of a n-by-n matrix using the QR decomposition. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
Here an example:
Definition at line 381 of file vpMatrix_qr.cpp.
References vpException::fatalError, and inverseByQRLapack().
Referenced by vpLinProg::simplex().
| vpMatrix vpMatrix::inverseByQRLapack | ( | ) | const |
Compute the inverse of a n-by-n matrix using the QR decomposition with Lapack 3rd party.
Here an example:
Definition at line 151 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::getRows(), vpMatrixException::matrixError, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by inverseByQR().
| vpMatrix vpMatrix::inverseTriangular | ( | bool | upper = true | ) | const |
Compute the inverse of a full-rank n-by-n triangular matrix. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| upper | : if it is an upper triangular matrix |
The function does not check if the matrix is actually upper or lower triangular.
Definition at line 1010 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpException::fatalError, vpMatrixException::rankDeficient, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
Juxtapose to matrices C = [ A B ].
![]()
| A | : Left matrix. |
| B | : Right matrix. |
Definition at line 5315 of file vpMatrix.cpp.
Referenced by vpLinProg::colReduction().
Juxtapose to matrices C = [ A B ].
![]()
| A | : Left matrix. |
| B | : Right matrix. |
| C | : Juxtaposed matrix C = [ A B ] |
Definition at line 5336 of file vpMatrix.cpp.
References vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), and vpArray2D< Type >::resize().
| unsigned int vpMatrix::kernel | ( | vpMatrix & | kerAt, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix ![]() .
.
The null space of a matrix ![]() is defined as
is defined as ![]() .
.
| kerAt | The matrix that contains the null space (kernel) of kerAt is (0, n), otherwise the dimension is (n-r, n). This matrix is thus the transpose of |
| svThreshold | Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Definition at line 6056 of file vpMatrix.cpp.
References getCol(), vpArray2D< double >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), vpColVector::sumSquare(), and svd().
Compute Kronecker product matrix.
| m | : vpMatrix; |
Definition at line 1958 of file vpMatrix.cpp.
References kron().
Compute Kronecker product matrix.
Definition at line 1927 of file vpMatrix.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
Compute Kronecker product matrix.
Definition at line 1889 of file vpMatrix.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
Compute Kronecker product matrix.
| m | : vpMatrix. |
| out | : If m1.kron(m2) out contains the kronecker product's result : |
Definition at line 1919 of file vpMatrix.cpp.
Referenced by kron().
|
inlinestaticinherited |
Load a matrix from a file.
| filename | : Absolute file name. |
| A | : Array to be loaded |
| binary | : If true the matrix is loaded from a binary file, else from a text file. |
| header | : Header of the file is loaded in this parameter. |
Definition at line 653 of file vpArray2D.h.
|
inlinestatic |
Load a matrix from a file. This function overloads vpArray2D::load().
| filename | : Absolute file name. |
| M | : Matrix to be loaded. |
| binary | : If true the matrix data are considered as binary, otherwise as human readable (text) data. Using binary data allows to keep data precision. |
| header | : Header of the file is loaded in this parameter. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.bin file where data are saved as binary data is the following:
% cat matrix.bin My header??@@@%
Definition at line 748 of file vpMatrix.h.
References vpArray2D< Type >::load().
Referenced by vpDot2::defineDots().
|
inlinestatic |
Load a matrix from a YAML-formatted file. This function overloads vpArray2D::loadYAML().
| filename | : Absolute YAML file name. |
| M | : Matrix to be loaded from the file. |
| header | : Header of the file is loaded in this parameter. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.yaml file is the following:
% cat matrix.yaml My header rows: 2 cols: 3 data: - [-1, -2, -3] - [4, 5.5, 6]
Definition at line 823 of file vpMatrix.h.
References vpArray2D< Type >::loadYAML().
|
inlinestaticinherited |
Load an array from a YAML-formatted file.
| filename | : absolute file name. |
| A | : array to be loaded from the file. |
| header | : header of the file is loaded in this parameter. |
Definition at line 767 of file vpArray2D.h.
| std::ostream & vpMatrix::maplePrint | ( | std::ostream & | os | ) | const |
Print using Maple syntax, to copy/paste in Maple later.
The following code
produces this output:
that could be copy/paste in Maple.
Definition at line 5548 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
| std::ostream & vpMatrix::matlabPrint | ( | std::ostream & | os | ) | const |
Print using Matlab syntax, to copy/paste in Matlab later.
The following code
produces this output:
that could be copy/paste in Matlab:
Definition at line 5501 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), and vpArray2D< double >::getRows().
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1189 of file vpMatrix.cpp.
References multMatrixVector().
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If matrices are not 4-by-4 dimension. |
Definition at line 1130 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
Definition at line 1035 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator*().
|
static |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If matrices are not 3-by-3 dimension. |
Definition at line 1093 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
|
static |
Operation w = A * v (v and w are vectors).
A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 984 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by mult2Matrices(), and operator*().
Operation C = -A.
The result is placed in the second parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 1617 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator-().
| unsigned int vpMatrix::nullSpace | ( | vpMatrix & | kerA, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix ![]() .
.
The null space of a matrix ![]() is defined as
is defined as ![]() .
.
| kerA | The matrix that contains the null space (kernel) of kerA is (n, 0), otherwise its dimension is (n, n-r). |
| svThreshold | Threshold used to test the singular values. The dimension of kerA corresponds to the number of singular values lower than this threshold |
Definition at line 6130 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), and svd().
Referenced by vpMeEllipse::leastSquare(), and vpMeEllipse::leastSquareRobust().
| unsigned int vpMatrix::nullSpace | ( | vpMatrix & | kerA, |
| int | dim | ||
| ) | const |
Function to compute the null space (the kernel) of a m-by-n matrix ![]() .
.
The null space of a matrix ![]() is defined as
is defined as ![]() .
.
| kerA | The matrix that contains the null space (kernel) of kerA is (n, 0), otherwise its dimension is (n, n-r). |
| dim | the dimension of the null space when it is known a priori |
Definition at line 6197 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), insert(), vpColVector::resize(), vpArray2D< Type >::resize(), and svd().
|
inherited |
Not equal to comparison operator of a 2D array.
Definition at line 509 of file vpArray2D.h.
| vpColVector vpMatrix::operator* | ( | const vpColVector & | v | ) | const |
Operation w = A * v (matrix A is unchanged, v and w are column vectors).
Definition at line 969 of file vpMatrix.cpp.
References multMatrixVector().
| vpMatrix vpMatrix::operator* | ( | const vpForceTwistMatrix & | V | ) | const |
Operator that allow to multiply a matrix by a force/torque twist matrix. The matrix should be of dimension m-by-6.
Definition at line 1327 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | const vpHomogeneousMatrix & | M | ) | const |
Operator that allow to multiply a matrix by a homogeneous matrix. The matrix should be of dimension m-by-4.
Definition at line 1241 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Operation C = A * B (A is unchanged).
Definition at line 1198 of file vpMatrix.cpp.
References mult2Matrices().
| vpMatrix vpMatrix::operator* | ( | const vpRotationMatrix & | R | ) | const |
Operator that allow to multiply a matrix by a rotation matrix. The matrix should be of dimension m-by-3.
Definition at line 1211 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpTranslationVector vpMatrix::operator* | ( | const vpTranslationVector & | tv | ) | const |
Operator that allows to multiply a matrix by a translation vector. The matrix should be of dimension (3x3)
Definition at line 943 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | const vpVelocityTwistMatrix & | V | ) | const |
Operator that allow to multiply a matrix by a velocity twist matrix. The matrix should be of dimension m-by-6.
Definition at line 1271 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator* | ( | double | x | ) | const |
Operator that allows to multiply all the elements of a matrix by a scalar.
Definition at line 1693 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator*= | ( | double | x | ) |
Multiply all the element of the matrix by x : Aij = Aij * x.
Operator that allows to multiply all the elements of a matrix by a scalar.
Definition at line 1764 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Operation C = A + B (A is unchanged).
Definition at line 1481 of file vpMatrix.cpp.
References add2Matrices().
Operation A = A + B.
Definition at line 1572 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, vpArray2D< double >::rowPtrs, and vpArray2D< Type >::rowPtrs.
| vpMatrix & vpMatrix::operator+= | ( | double | x | ) |
Add x to all the element of the matrix : Aij = Aij + x.
Definition at line 1737 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator, | ( | double | val | ) |
Definition at line 827 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator- | ( | void | ) | const |
Operation C = -A (A is unchanged).
Definition at line 1637 of file vpMatrix.cpp.
References negateMatrix().
Operation C = A - B (A is unchanged).
Definition at line 1563 of file vpMatrix.cpp.
References sub2Matrices().
Operation A = A - B.
Definition at line 1591 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::rowNum, vpArray2D< double >::rowPtrs, and vpArray2D< Type >::rowPtrs.
| vpMatrix & vpMatrix::operator-= | ( | double | x | ) |
subtract x to all the element of the matrix : Aij = Aij - x
Definition at line 1749 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix vpMatrix::operator/ | ( | double | x | ) | const |
Cij = Aij / x (A is unchanged)
Definition at line 1712 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::divideByZeroError, vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator/= | ( | double | x | ) |
Divide all the element of the matrix by x : Aij = Aij / x.
Definition at line 1780 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::divideByZeroError, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator<< | ( | double * | x | ) |
Assignment from an array of double. This method has to be used carefully since the array allocated behind x pointer should have the same dimension than the matrix.
Definition at line 810 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator<< | ( | double | val | ) |
Definition at line 820 of file vpMatrix.cpp.
References vpArray2D< double >::resize(), and vpArray2D< double >::rowPtrs.
| vpMatrix & vpMatrix::operator= | ( | const std::initializer_list< double > & | list | ) |
Set matrix elements from a list of values.
| list | : List of double. Matrix size (number of columns multiplied by number of columns) should match the number of elements. |
It produces the following printings:
Definition at line 745 of file vpMatrix.cpp.
References vpArray2D< double >::data, vpArray2D< double >::dsize, and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | const std::initializer_list< std::initializer_list< double > > & | lists | ) |
Set matrix elements from a list of values.
| lists | : List of double. |
Definition at line 779 of file vpMatrix.cpp.
References vpArray2D< double >::resize(), vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Copy operator that allows to convert on of the following container that inherit from vpArray2D such as vpMatrix, vpRotationMatrix, vpHomogeneousMatrix, vpPoseVector, vpColVector, vpRowVector... into a vpMatrix.
| A | : 2D array to be copied. |
The following example shows how to create a matrix from an homogeneous matrix:
Definition at line 670 of file vpMatrix.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
Definition at line 681 of file vpMatrix.cpp.
References vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< double >::dsize, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< double >::resize().
| vpMatrix & vpMatrix::operator= | ( | double | x | ) |
Set all the element of the matrix A to x.
Definition at line 799 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, and vpArray2D< double >::rowNum.
Definition at line 693 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< double >::dsize, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Equal to comparison operator of a 2D array.
Definition at line 505 of file vpArray2D.h.
|
inlineinherited |
Set element 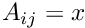 using A[i][j] = x.
using A[i][j] = x.
Definition at line 591 of file vpArray2D.h.
|
inlineinherited |
Get element 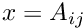 using x = A[i][j].
using x = A[i][j].
Definition at line 593 of file vpArray2D.h.
| int vpMatrix::print | ( | std::ostream & | s, |
| unsigned int | length, | ||
| const std::string & | intro = "" |
||
| ) | const |
Pretty print a matrix. The data are tabulated. The common widths before and after the decimal point are set with respect to the parameter length.
| s | : Stream used for the printing. |
| length | : The suggested width of each matrix element. If needed, the used length grows in order to accommodate the whole integral part, and shrinks the decimal part to print only length digits. |
| intro | : The introduction which is printed before the matrix. Can be set to zero (or omitted), in which case the introduction is not printed. |
Definition at line 5382 of file vpMatrix.cpp.
References vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpMath::maximum(), and vpArray2D< double >::size().
Referenced by vpServo::computeControlLaw().
|
inline |
Definition at line 584 of file vpMatrix.h.
References vpArray2D< Type >::getCols(), and vpArray2D< Type >::getRows().
| vpMatrix vpMatrix::pseudoInverse | ( | double | svThreshold = 1e-6 | ) | const |
Compute and return the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() .
.
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2343 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
Referenced by vpSimulatorAfma6::computeArticularVelocity(), vpSimulatorViper850::computeArticularVelocity(), vpServo::computeControlLaw(), computeCovarianceMatrix(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpMbTracker::computeVVSPoseEstimation(), vpQuadProg::fromCanonicalCost(), vpNurbs::globalCurveApprox(), vpNurbs::globalCurveInterp(), vpHomography::inverse(), vpMeLine::leastSquare(), vpHomogeneousMatrix::mean(), vpRotationMatrix::mean(), vpPose::poseDementhonNonPlan(), vpPose::poseDementhonPlan(), vpPose::poseFromRectangle(), pseudoInverse(), vpHomography::robust(), solveBySVD(), and vpQuadProg::solveQPi().
| vpMatrix vpMatrix::pseudoInverse | ( | int | rank_in | ) | const |
Compute and return the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() .
.
| [in] | rank_in | : Known rank of the matrix. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2408 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2201 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse | |
| [in] | rank_in | : Known rank of the matrix. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 2277 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
See pseudoInverse(vpMatrix &, vpColVector &, double, vpMatrix &, vpMatrix &, vpMatrix &) const for a complete description of this function.
| Ap | : The Moore-Penros pseudo inverse |
| sv | Vector corresponding to matrix |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
| imA | |
| imAt |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4543 of file vpMatrix.cpp.
References pseudoInverse().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() ,
, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse |
| sv | : Vector corresponding to matrix A singular values. The size of this vector is equal to min(m, n). |
| svThreshold | : Threshold used to test the singular values.If a singular value is lower than this threshold we consider that the matrix is not full rank. |
| imA | : |
| imAt | : |
| kerAt | : The matrix that contains the null space(kernel) of kerAt is(0, n), otherwise the dimension is (n - r, n). This matrix is thus the transpose of |
Here an example to compute the pseudo - inverse of a 2 - by - 3 matrix that is rank 2.
Once build, the previous example produces the following output :
Definition at line 4734 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| unsigned int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values and return the rank of the matrix.
along with singular values and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse |
| sv | Vector corresponding to matrix |
| svThreshold | : Threshold used to test the singular values. If a singular value is lower than this threshold we consider that the matrix is not full rank. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4370 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values and return the rank of the matrix.
along with singular values and return the rank of the matrix.
| Ap | : The Moore-Penros pseudo inverse | |
| sv | Vector corresponding to matrix | |
| [in] | rank_in | : Known rank of the matrix. |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4453 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
See pseudoInverse(vpMatrix &, vpColVector &, double, vpMatrix &, vpMatrix &, vpMatrix &) const for a complete description of this function.
| Ap | : The Moore-Penros pseudo inverse | |
| sv | Vector corresponding to matrix | |
| [in] | rank_in | : Known rank of the matrix. |
| imA | ||
| imAt |
Here an example to compute the pseudo-inverse of a 2-by-3 matrix that is rank 2.
Once build, the previous example produces the following output:
Definition at line 4627 of file vpMatrix.cpp.
References pseudoInverse().
| int vpMatrix::pseudoInverse | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
Compute the Moore-Penros pseudo inverse ![]() of a m-by-n matrix
of a m-by-n matrix ![]() along with singular values,
along with singular values, ![]() ,
, ![]() and
and ![]() and return the rank of the matrix.
and return the rank of the matrix.
| Ap | : The Moore - Penros pseudo inverse | |
| sv | : Vector corresponding to matrix | |
| [in] | rank_in | : Known rank of the matrix. |
| imA | : | |
| imAt | : | |
| kerAt | : The matrix that contains the null space(kernel) of kerAt is(0, n), otherwise the dimension is(n - r, n).This matrix is thus the transpose of |
Here an example to compute the pseudo - inverse of a 2 - by - 3 matrix that is rank 2.
Once build, the previous example produces the following output :
Definition at line 4861 of file vpMatrix.cpp.
References vpException::fatalError, pseudoInverseEigen3(), pseudoInverseLapack(), and pseudoInverseOpenCV().
| vpMatrix vpMatrix::pseudoInverseEigen3 | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| vpMatrix vpMatrix::pseudoInverseEigen3 | ( | int | rank_in | ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseEigen3 | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseLapack | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| vpMatrix vpMatrix::pseudoInverseLapack | ( | int | rank_in | ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseLapack | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| vpMatrix vpMatrix::pseudoInverseOpenCV | ( | double | svThreshold = 1e-6 | ) | const |
Referenced by pseudoInverse().
| vpMatrix vpMatrix::pseudoInverseOpenCV | ( | int | rank_in | ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| int | rank_in | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| double | svThreshold = 1e-6 |
||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in | ||
| ) | const |
| int vpMatrix::pseudoInverseOpenCV | ( | vpMatrix & | Ap, |
| vpColVector & | sv, | ||
| int | rank_in, | ||
| vpMatrix & | imA, | ||
| vpMatrix & | imAt, | ||
| vpMatrix & | kerAt | ||
| ) | const |
| unsigned int vpMatrix::qr | ( | vpMatrix & | Q, |
| vpMatrix & | R, | ||
| bool | full = false, |
||
| bool | squareR = false, |
||
| double | tol = 1e-6 |
||
| ) | const |
Compute the QR decomposition of a (m x n) matrix of rank r. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| Q | : orthogonal matrix (will be modified). |
| R | : upper-triangular matrix (will be modified). |
| full | : whether or not we want full decomposition. |
| squareR | : will return only the square (min(m,n) x min(m,n)) part of R. |
| tol | : tolerance to test the rank of R. |
If full is false (default) then Q is (m x min(n,m)) and R is (min(n,m) x n). We then have this = QR.
If full is true and m > n then Q is (m x m) and R is (n x n). In this case this = Q (R, 0)^T
If squareR is true and n > m then R is (m x m). If r = m then R is invertible.
Here an example:
Definition at line 444 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction().
| unsigned int vpMatrix::qrPivot | ( | vpMatrix & | Q, |
| vpMatrix & | R, | ||
| vpMatrix & | P, | ||
| bool | full = false, |
||
| bool | squareR = false, |
||
| double | tol = 1e-6 |
||
| ) | const |
Compute the QR pivot decomposition of a (m x n) matrix of rank r. Only available if Lapack 3rd party is installed. If Lapack is not installed we use a Lapack built-in version.
| Q | : orthogonal matrix (will be modified). |
| R | : upper-triangular matrix (will be modified). |
| P | : the (n x n) permutation matrix. |
| full | : whether or not we want full decomposition. |
| squareR | : will return only the (r x r) part of R and the (r x n) part of P. |
| tol | : tolerance to test the rank of R. |
If full is false (default) then Q is (m x min(n,m)) and R is (min(n,m) x n). We then have this.P = Q.R.
If full is true and m > n then Q is (m x m) and R is (n x n). In this case this.P = Q (R, 0)^T
If squareR is true then R is (r x r) invertible.
Here an example:
Definition at line 726 of file vpMatrix_qr.cpp.
References vpException::badValue, vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< double >::rowNum.
Referenced by vpLinProg::colReduction(), vpLinProg::rowReduction(), and solveByQR().
|
inlineinherited |
Definition at line 443 of file vpArray2D.h.
|
inlineinherited |
Set the size of the array and initialize all the values to zero.
| nrows | : number of rows. |
| ncols | : number of column. |
| flagNullify | : if true, then the array is re-initialized to 0 after resize. If false, the initial values from the common part of the array (common part between old and new version of the array) are kept. Default value is true. |
| recopy_ | : if true, will perform an explicit recopy of the old data. |
Definition at line 352 of file vpArray2D.h.
| vpRowVector vpMatrix::row | ( | unsigned int | i | ) |
should be replaced with:
| i | : Index of the row to extract noting that row index start at 1 to get the first row. |
Definition at line 6653 of file vpMatrix.cpp.
References vpArray2D< double >::getCols().
|
inlinestaticinherited |
Save a matrix to a file.
| filename | : Absolute file name. |
| A | : Array to be saved. |
| binary | : If true the matrix is saved in a binary file, else a text file. |
| header | : Optional line that will be saved at the beginning of the file. |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 855 of file vpArray2D.h.
|
inlinestatic |
Save a matrix to a file. This function overloads vpArray2D::save().
| filename | : Absolute file name. |
| M | : Matrix to be saved. |
| binary | : If true the matrix is save as a binary file, otherwise as a text file. |
| header | : Optional line that will be saved at the beginning of the file as a header. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.bin My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.bin file where data are saved as binary data is the following:
% cat matrix.bin My header??@@@%
Definition at line 896 of file vpMatrix.h.
References vpArray2D< Type >::save().
Referenced by vpDot2::defineDots().
|
inlinestatic |
Save a matrix in a YAML-formatted file. This function overloads vpArray2D::saveYAML().
| filename | : Absolute file name. |
| M | : Matrix to be saved in the file. |
| header | : Optional lines that will be saved at the beginning of the file as a header. |
The following example shows how to use this function:
The output of this example is the following:
Matrix saved in matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0 Matrix loaded from matrix.yaml My header[2,3]= -1.0 -2.0 -3.0 4.0 5.5 6.0
And the content of matrix.yaml file is the following:
% cat matrix.yaml My header rows: 2 cols: 3 data: - [-1, -2, -3] - [4, 5.5, 6]
Definition at line 972 of file vpMatrix.h.
References vpArray2D< Type >::saveYAML().
|
inlinestaticinherited |
Save an array in a YAML-formatted file.
| filename | : absolute file name. |
| A | : array to be saved in the file. |
| header | : optional lines that will be saved at the beginning of the file. Should be YAML-formatted and will adapt to the indentation if any. |
Here is an example of outputs.
Content of matrix.yml:
Content of matrixIndent.yml:
Definition at line 950 of file vpArray2D.h.
| void vpMatrix::setIdentity | ( | const double & | val = 1.0 | ) |
Set the matrix diagonal elements to val. More generally set M[i][i] = val.
Definition at line 6696 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
Referenced by vpServo::secondaryTask().
|
inlinestatic |
Modify default size used to determine if Blas/Lapack basic linear algebra operations are enabled.
To get more info see Tutorial: Basic linear algebra operations.
| min_size | : Minimum size of rows and columns required for a matrix or a vector to use Blas/Lapack third parties like MKL, OpenBLAS, Netlib or Atlas. When matrix or vector size is lower or equal to this parameter, Blas/Lapack is not used. In that case we prefer use naive code that runs faster for small matrices. |
Definition at line 250 of file vpMatrix.h.
|
inlineinherited |
Return the number of elements of the 2D array.
Definition at line 339 of file vpArray2D.h.
| vpColVector vpMatrix::solveByQR | ( | const vpColVector & | b | ) | const |
Solve a linear system Ax = b using QR Decomposition.
Non destructive wrt. A and B.
| b | : Vector b |
Here an example:
Definition at line 1205 of file vpMatrix_qr.cpp.
References vpArray2D< double >::colNum, and solveByQR().
| void vpMatrix::solveByQR | ( | const vpColVector & | b, |
| vpColVector & | x | ||
| ) | const |
Solve a linear system Ax = b using QR Decomposition.
Non destructive wrt. A and b.
| b | : Vector b |
| x | : Vector x |
Here an example:
Definition at line 1155 of file vpMatrix_qr.cpp.
References vpArray2D< double >::colNum, extract(), inverseTriangular(), qrPivot(), and t().
Referenced by solveByQR(), and vpQuadProg::solveSVDorQR().
| vpColVector vpMatrix::solveBySVD | ( | const vpColVector & | B | ) | const |
Solve a linear system ![]() using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| B | : Vector |
Here an example:
Definition at line 2061 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and solveBySVD().
| void vpMatrix::solveBySVD | ( | const vpColVector & | b, |
| vpColVector & | x | ||
| ) | const |
Solve a linear system ![]() using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| b | : Vector |
| x | : Vector |
Here an example:
Definition at line 2010 of file vpMatrix.cpp.
References pseudoInverse().
Referenced by vpMeEllipse::leastSquare(), vpMeEllipse::leastSquareRobust(), vpQuadProg::solveByProjection(), solveBySVD(), vpQuadProg::solveQPe(), and vpQuadProg::solveSVDorQR().
| void vpMatrix::stack | ( | const vpColVector & | c | ) |
Stack column vector c at the right of the current matrix, or copy if the matrix has no dimensions: this = [ this c ].
Here an example for a robot velocity log matrix:
Here the log matrix has size 6 rows by 100 columns.
Definition at line 5742 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, vpArray2D< Type >::getRows(), vpArray2D< double >::resize(), vpArray2D< double >::rowNum, vpArray2D< double >::rowPtrs, and vpArray2D< Type >::size().
| void vpMatrix::stack | ( | const vpMatrix & | A | ) |
Stack A at the end of the current matrix, or copy if the matrix has no dimensions : this = [ this A ]^T.
Definition at line 5669 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), insert(), vpArray2D< double >::resize(), and vpArray2D< double >::rowNum.
Referenced by vpFeatureVanishingPoint::interaction(), vpFeatureEllipse::interaction(), vpFeaturePoint::interaction(), vpFeaturePoint3D::interaction(), vpFeaturePointPolar::interaction(), vpFeatureSegment::interaction(), vpFeatureThetaU::interaction(), vpFeatureTranslation::interaction(), vpGenericFeature::interaction(), vpLinProg::rowReduction(), stack(), vpColVector::stackMatrices(), and stackMatrices().
|
static |
Stack column vector c to matrix A and return the resulting matrix [ A c ]
| A | : Left matrix. |
| c | : Right column vector. |
Definition at line 5231 of file vpMatrix.cpp.
References stack().
|
static |
Stack column vector c to the end of matrix A and return the resulting matrix in C.
| A | : Left matrix. |
| c | : Right column vector. |
| C | : Stacked matrix C = [ A c ] |
Definition at line 5250 of file vpMatrix.cpp.
References vpArray2D< Type >::data, and stack().
Stack matrix B to the end of matrix A and return the resulting matrix [ A B ]^T
| A | : Upper matrix. |
| B | : Lower matrix. |
Definition at line 5128 of file vpMatrix.cpp.
References stack().
Stack matrix B to the end of matrix A and return the resulting matrix in C.
| A | : Upper matrix. |
| B | : Lower matrix. |
| C | : Stacked matrix C = [ A B ]^T |
Definition at line 5148 of file vpMatrix.cpp.
References vpArray2D< Type >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), and vpArray2D< Type >::size().
|
static |
Stack row vector r to matrix A and return the resulting matrix [ A r ]^T
| A | : Upper matrix. |
| r | : Lower row vector. |
Definition at line 5192 of file vpMatrix.cpp.
References stack().
|
static |
Stack row vector r to the end of matrix A and return the resulting matrix in C.
| A | : Upper matrix. |
| r | : Lower row vector. |
| C | : Stacked matrix C = [ A r ]^T |
Definition at line 5211 of file vpMatrix.cpp.
References vpArray2D< Type >::data, and stack().
| void vpMatrix::stack | ( | const vpRowVector & | r | ) |
Stack row vector r at the end of the current matrix, or copy if the matrix has no dimensions: this = [ this r ]^T.
Here an example for a robot velocity log :
Definition at line 5701 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< double >::resize(), vpArray2D< double >::rowNum, vpArray2D< double >::size(), and vpArray2D< Type >::size().
| vpColVector vpMatrix::stackColumns | ( | ) |
Stacks columns of a matrix in a vector.
Definition at line 1827 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
| void vpMatrix::stackColumns | ( | vpColVector & | out | ) |
Stacks columns of a matrix in a vector.
| out | : a vpColVector. |
Definition at line 1809 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpArray2D< double >::colNum, vpArray2D< Type >::data, vpColVector::resize(), vpArray2D< double >::rowNum, vpArray2D< Type >::rowNum, and vpArray2D< double >::rowPtrs.
|
static |
Definition at line 6621 of file vpMatrix.cpp.
References vpColVector::stack().
|
static |
Definition at line 6626 of file vpMatrix.cpp.
References vpColVector::stack().
|
inline |
Definition at line 994 of file vpMatrix.h.
|
inlinestatic |
Definition at line 999 of file vpMatrix.h.
|
inlinestatic |
Definition at line 1004 of file vpMatrix.h.
|
static |
Definition at line 6631 of file vpMatrix.cpp.
References stack().
|
static |
Definition at line 6633 of file vpMatrix.cpp.
References stack().
| vpRowVector vpMatrix::stackRows | ( | ) |
Stacks rows of a matrix in a vector.
Definition at line 1850 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, and vpArray2D< double >::rowNum.
| void vpMatrix::stackRows | ( | vpRowVector & | out | ) |
Stacks rows of a matrix in a vector
| out | : a vpRowVector. |
Definition at line 1838 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::data, vpArray2D< Type >::data, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpRowVector::resize(), and vpArray2D< double >::rowNum.
|
static |
Operation C = A - B on column vectors.
The result is placed in the third parameter C and not returned. A new vector won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If A and B vectors have not the same size. |
Definition at line 1503 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Operation C = A - B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (speed gain if used many times with the same result matrix size).
| vpException::dimensionError | If A and B matrices have not the same size. |
Definition at line 1537 of file vpMatrix.cpp.
References vpArray2D< Type >::colNum, vpException::dimensionError, vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpArray2D< Type >::rowNum, and vpArray2D< Type >::rowPtrs.
Referenced by operator-().
| double vpMatrix::sum | ( | ) | const |
Return the sum of all the  elements of the matrix.
elements of the matrix.
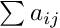
Definition at line 1644 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
Referenced by expm().
| double vpMatrix::sumSquare | ( | ) | const |
Return the sum square of all the ![]() elements of the matrix
elements of the matrix ![]() .
.
Definition at line 6595 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< double >::rowNum, and vpArray2D< double >::rowPtrs.
| void vpMatrix::svd | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Matrix singular value decomposition (SVD).
This function calls the first following function that is available:
If none of these previous 3rd parties is installed, we use by default svdLapack() with a Lapack built-in version.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object `(*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 2132 of file vpMatrix.cpp.
References vpException::fatalError, svdEigen3(), svdLapack(), and svdOpenCV().
Referenced by vpHomogeneousMatrix::compute3d3dTransformation(), cond(), vpHomography::DLT(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), inducedL2Norm(), kernel(), nullSpace(), vpRotationMatrix::orthogonalize(), and svdEigen3().
| void vpMatrix::svdEigen3 | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using Eigen3 3rd party.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object (*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 439 of file vpMatrix_svd.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< double >::getCols(), vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpArray2D< double >::getRows(), vpColVector::resize(), vpArray2D< double >::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, vpArray2D< Type >::size(), and svd().
Referenced by svd().
| void vpMatrix::svdLapack | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using Lapack 3rd party.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object (*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 236 of file vpMatrix_svd.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpException::fatalError, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpColVector::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::rowNum, and transpose().
Referenced by svd().
| void vpMatrix::svdOpenCV | ( | vpColVector & | w, |
| vpMatrix & | V | ||
| ) |
Singular value decomposition (SVD) using OpenCV 3rd party.
Given matrix ![]() , this function computes it singular value decomposition such as
, this function computes it singular value decomposition such as
![]()
| w | : Vector of singular values: |
| V | : Matrix |
The matrix object (*this) is updated with ![]() .
.
Here an example of SVD decomposition of a non square Matrix M.
Definition at line 149 of file vpMatrix_svd.cpp.
References vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< double >::getCols(), vpArray2D< double >::getRows(), vpColVector::resize(), vpArray2D< Type >::resize(), vpArray2D< double >::resize(), and transpose().
Referenced by svd().
| vpMatrix vpMatrix::t | ( | ) | const |
Compute and return the transpose of the matrix.
Definition at line 465 of file vpMatrix.cpp.
References transpose().
Referenced by vpLinProg::colReduction(), vpHomogeneousMatrix::compute3d3dTransformation(), vpServo::computeControlLaw(), computeCovarianceMatrix(), vpTemplateTracker::computeOptimalBrentGain(), eigenValues(), vpMbtFaceDepthNormal::estimatePlaneEquationSVD(), vpKalmanFilter::filtering(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpQuadProg::fromCanonicalCost(), vpHomogeneousMatrix::mean(), vpRotationMatrix::mean(), vpRotationMatrix::orthogonalize(), vpKalmanFilter::prediction(), vpLinProg::simplex(), and solveByQR().
| vpMatrix vpMatrix::transpose | ( | ) | const |
Compute and return the transpose of the matrix.
Definition at line 472 of file vpMatrix.cpp.
Referenced by vpLinProg::colReduction(), vpQuadProg::fromCanonicalCost(), vpLinProg::rowReduction(), vpLinProg::solveLP(), vpQuadProg::solveQPi(), svdLapack(), svdOpenCV(), and t().
| void vpMatrix::transpose | ( | vpMatrix & | At | ) | const |
Compute At the transpose of the matrix.
| At | (output) : Resulting transpose matrix. |
Definition at line 484 of file vpMatrix.cpp.
References vpArray2D< double >::colNum, vpArray2D< Type >::data, vpArray2D< double >::data, vpArray2D< Type >::resize(), and vpArray2D< double >::rowNum.
|
related |
Insert array B in array A at the given position.
| A | : Main array. |
| B | : Array to insert. |
| C | : Result array. |
| r | : Index of the row where to insert array B. |
| c | : Index of the column where to insert array B. |
Definition at line 1072 of file vpArray2D.h.
|
related |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| C | : Result matrix. |
| r | : Index of the row where to insert matrix B. |
| c | : Index of the column where to insert matrix B. |
Definition at line 5295 of file vpMatrix.cpp.
|
related |
Definition at line 1300 of file vpArray2D.h.
Allow to multiply a scalar by a matrix.
Definition at line 1668 of file vpMatrix.cpp.
References vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), and vpArray2D< Type >::resize().
|
related |
Definition at line 1264 of file vpArray2D.h.
|
related |
Definition at line 1282 of file vpArray2D.h.
|
related |
This function performs generalized matrix multiplication: D = alpha*op(A)*op(B) + beta*op(C), where op(X) is X or X^T. Operation on A, B and C matrices is described by enumeration vpGEMMmethod().
For example, to compute D = alpha*A^T*B^T+beta*C we need to call :
If C is not used, vpGEMM must be called using an empty array null. Thus to compute D = alpha*A^T*B, we have to call:
| vpException::incorrectMatrixSizeError | if the sizes of the matrices do not allow the operations. |
| A | : An array that could be a vpMatrix. |
| B | : An array that could be a vpMatrix. |
| alpha | : A scalar. |
| C | : An array that could be a vpMatrix. |
| beta | : A scalar. |
| D | : The resulting array that could be a vpMatrix. |
| ops | : A scalar describing operation applied on the matrices. Possible values are the one defined in vpGEMMmethod(): VP_GEMM_A_T, VP_GEMM_B_T, VP_GEMM_C_T. |
|
related |
Enumeration of the operations applied on matrices in vpGEMM() function.
Operations are :
|
protectedinherited |
Number of columns in the array.
Definition at line 131 of file vpArray2D.h.
|
inherited |
Address of the first element of the data array.
Definition at line 139 of file vpArray2D.h.
|
protectedinherited |
Current array size (rowNum * colNum)
Definition at line 135 of file vpArray2D.h.
|
protectedinherited |
Number of rows in the array.
Definition at line 129 of file vpArray2D.h.
|
protectedinherited |
Address of the first element of each rows.
Definition at line 133 of file vpArray2D.h.