Visual Servoing Platform  version 3.2.0 under development (2019-01-22)
Public Types | List of all members
vpLinProg Class Reference
core: Core module » Tools » Optimization

#include <visp3/core/vpLinProg.h>

Public Types

typedef std::pair< unsigned int, double > BoundedIndex
 

Static Public Member Functions

Solvers
static bool simplex (const vpColVector &c, vpMatrix A, vpColVector b, vpColVector &x, const double &tol=1e-6)
 
static bool solveLP (const vpColVector &c, vpMatrix A, vpColVector b, const vpMatrix &C, const vpColVector &d, vpColVector &x, std::vector< BoundedIndex > l={}, std::vector< BoundedIndex > u={}, const double &tol=1e-6)
 
Dimension reduction for equality constraints
static bool colReduction (vpMatrix &A, vpColVector &b, bool full_rank=false, const double &tol=1e-6)
 
static bool rowReduction (vpMatrix &A, vpColVector &b, const double &tol=1e-6)
 
Vector and equality checking
static bool allZero (const vpColVector &x, const double &tol=1e-6)
 
static bool allClose (const vpMatrix &A, const vpColVector &x, const vpColVector &b, const double &tol=1e-6)
 
static bool allLesser (const vpMatrix &C, const vpColVector &x, const vpColVector &d, const double &thr=1e-6)
 
static bool allLesser (const vpColVector &x, const double &thr=1e-6)
 
static bool allGreater (const vpColVector &x, const double &thr=1e-6)
 

Detailed Description

This class provides two solvers for Linear Programs.

One is a classical simplex, the other can deal with various inequality or bound constraints.

Utility functions to reduce or check linear equalities or inequalities are also available.

Warning
The solvers are only available if C++11 is activated during compilation. Configure ViSP using cmake -DUSE_CPP11=ON.

Definition at line 65 of file vpLinProg.h.

Member Typedef Documentation

typedef std::pair<unsigned int, double> vpLinProg::BoundedIndex

Used to pass a list of bounded variables to solveLP(), as a list of (index, bound).

The type is compatible with C++11's braced initialization. Construction can be done in the call to solveLP or before, as shown in this example:

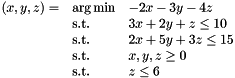
$\begin{array}{lll} (x,y,z) = & \arg\min & -2x -3y -4z\\ & \text{s.t.}& 3x + 2y + z \leq 10\\ & \text{s.t.}& 2x + 5y + 3z \leq 15\\ & \text{s.t.}& x, y, z \geq 0\\ & \text{s.t.}& z \leq 6\end{array}$

Here the lower bound is built explicitely while the upper one is built during the call to solveLP():

Warning
This function is only available if C++11 is activated during compilation. Configure ViSP using cmake -DUSE_CPP11=ON.
#include <visp3/core/vpLinProg.h>
int main()
{
vpColVector c(3), x;
vpMatrix C(2, 3);
vpColVector d(2);
c[0] = -2; c[1] = -3; c[2] = -4;
C[0][0] = 3; C[0][1] = 2; C[0][2] = 1; d[0] = 10;
C[1][0] = 2; C[1][1] = 5; C[1][2] = 3; d[1] = 15;
// build lower bounds explicitely as a std::vector of std::pair<int, double>
std::vector<vpLinProg::BoundedIndex> lower_bound;
for(unsigned int i = 0; i < 3; ++i)
{
vpLinProg::BoundedIndex bound;
bound.first = i; // index
bound.second = 0; // lower bound for this index
lower_bound.push_back(bound);
}
if(vpLinProg::solveLP(c, vpMatrix(0,0), vpColVector(0), C, d, x,
lower_bound,
{{2,6}})) // upper bound is passed with braced initialization
{
std::cout << "x: " << x.t() << std::endl;
std::cout << "cost: " << c.t()*x << std::endl;
}
}
See also
solveLP()

Definition at line 121 of file vpLinProg.h.

Member Function Documentation

static bool vpLinProg::allClose ( const vpMatrix &  A,
const vpColVector &  x,
const vpColVector &  b,
const double &  tol = 1e-6 
)
inlinestatic

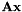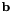Check if $\mathbf{A}\mathbf{x}$ is near $\mathbf{b}$.

Parameters
A: matrix (dimension m x n)
x: vector (dimension n)
b: vector (dimension m)
tol: tolerance
Returns
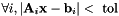
True if $ \forall i, |\mathbf{A}_i\mathbf{x} - \mathbf{b}_i| < \text{~tol}$

Definition at line 174 of file vpLinProg.h.

References vpMatrix::getRow(), and vpArray2D< Type >::getRows().

Referenced by colReduction(), rowReduction(), simplex(), and solveLP().

static bool vpLinProg::allGreater ( const vpColVector &  x,
const double &  thr = 1e-6 
)
inlinestatic

Check if all elements of 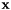$\mathbf{x}$ are greater or equal to threshold.

Parameters
x: vector (dimension n)
thr: threshold
Returns
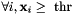
True if $ \forall i, \mathbf{x}_i \geq \text{~thr}$

Definition at line 229 of file vpLinProg.h.

References vpArray2D< Type >::getRows().

Referenced by simplex(), and vpQuadProg::solveQPi().

static bool vpLinProg::allLesser ( const vpMatrix &  C,
const vpColVector &  x,
const vpColVector &  d,
const double &  thr = 1e-6 
)
inlinestatic

Check if all elements of 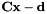$\mathbf{C}\mathbf{x} - \mathbf{d}$ are lesser or equal to threshold.

Parameters
C: matrix (dimension m x n)
x: vector (dimension n)
d: vector (dimension m)
thr: threshold
Returns
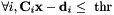
True if $ \forall i, \mathbf{C}_i\mathbf{x} - \mathbf{d}_i \leq \text{~thr}$

Definition at line 193 of file vpLinProg.h.

References vpMatrix::getRow(), and vpArray2D< Type >::getRows().

Referenced by simplex(), solveLP(), vpQuadProg::solveQP(), and vpQuadProg::solveQPi().

static bool vpLinProg::allLesser ( const vpColVector &  x,
const double &  thr = 1e-6 
)
inlinestatic

Check if all elements of 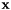$\mathbf{x}$ are lesser or equal to threshold.

Parameters
x: vector (dimension n)
thr: threshold
Returns
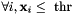
True if $ \forall i, \mathbf{x}_i \leq \text{~thr}$

Definition at line 211 of file vpLinProg.h.

References vpArray2D< Type >::getRows().

static bool vpLinProg::allZero ( const vpColVector &  x,
const double &  tol = 1e-6 
)
inlinestatic

Check if all elements of 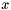$x$ are near zero.

Parameters
x: vector to be checked
tol: tolerance
Returns
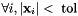
True if $\forall i, |\mathbf{x}_i| < \text{~tol} $

Definition at line 154 of file vpLinProg.h.

References vpArray2D< Type >::getRows().

Referenced by colReduction(), and vpQuadProg::solveQPi().

bool vpLinProg::colReduction ( vpMatrix &  A,
vpColVector &  b,
bool  full_rank = false,
const double &  tol = 1e-6 
)
static

Reduces the search space induced by an equality constraint.

Changes A and b so that the constraint 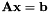$\mathbf{A}\mathbf{x} = \mathbf{b}$ can be written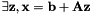 $\exists\mathbf{z}, \mathbf{x} = \mathbf{b} + \mathbf{A}\mathbf{z}$

This method is destructive for A and b.

Parameters
A: in = equality matrix (dimension m x n), out = projector to kernel (dimension n x (n-rank(A)))
b: in = equality vector (dimension m), out = particular solution (dimension n)
full_rank: if we think A is full rank, leads to a faster result but a slower one if A is actually not full rank.
tol: tolerance to test the ranks
Returns
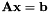True if $\mathbf{A}\mathbf{x} = \mathbf{b}$ has a solution.

Here is an example with $\mathbf{A} = \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 1 & 1& 0 & 0\end{array}\right]$ and $\mathbf{b} = \left[\begin{array}{c}1\\2\\3\end{array}\right]$ that become $\mathbf{A} = \left[\begin{array}{cc}0 & 0\\ 0 & 0\\ 1& 0\\ 0& 1\end{array}\right]$ and $\mathbf{b} = \left[\begin{array}{c}1\\2\\0\\0\end{array}\right]$.

We indeed have $\forall \mathbf{z}\in\mathbb{R}^2, \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 1 & 1& 0 & 0\end{array}\right] \left(\left[\begin{array}{c}1\\2\\0\\0\end{array}\right] + \left[\begin{array}{cc}0 & 0\\ 0 & 0\\ 1& 0\\ 0& 1\end{array}\right]\mathbf{z}\right) = \left[\begin{array}{c}1\\2\\3\end{array}\right]$

#include <visp3/core/vpLinProg.h>
int main()
{
vpMatrix A(3,4);
vpColVector b(3);
A[0][0] = A[1][1] = 1;
A[2][0] = A[2][1] = 1;
b[0] = 1; b[1] = 2; b[2] = 3;
vpMatrix Z = A;
vpColVector x1 = b;
if(vpLinProg::colReduction(Z, x1))
{
// Z is now 4 x 2
// try with random z-vector
vpColVector z(2);
for(int i = 0; i < 10; ++i)
{
z[0] = (10.*rand())/RAND_MAX;
z[1] = (10.*rand())/RAND_MAX;
std::cout << "A.(x1 + Z.z): " << (A*(x1 + Z*z)).t() << std::endl;
}
}
else
std::cout << "Ax = b not feasible\n";
}

Definition at line 97 of file vpLinProg.cpp.

References allClose(), allZero(), vpColVector::extract(), vpMatrix::extract(), vpMatrix::eye(), vpMatrix::getCol(), vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpColVector::infinityNorm(), vpMatrix::infinityNorm(), vpMatrix::inverseTriangular(), vpMatrix::juxtaposeMatrices(), vpMatrix::qr(), vpMatrix::qrPivot(), vpArray2D< Type >::resize(), vpColVector::resize(), vpMatrix::t(), and vpMatrix::transpose().

Referenced by vpQuadProg::setEqualityConstraint(), vpQuadProg::solveByProjection(), solveLP(), and vpQuadProg::solveQP().

bool vpLinProg::rowReduction ( vpMatrix &  A,
vpColVector &  b,
const double &  tol = 1e-6 
)
static

Reduces the number of equality constraints.

Changes A and b so that the constraint 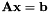$\mathbf{A}\mathbf{x} = \mathbf{b}$ is written with minimal rows.

This method is destructive for A and b.

Parameters
A: equality matrix (dimension in = (m x n), out = (rank(A) x n)
b: equality vector (dimension in = (m), out = (rank(A)))
tol: tolerance to test the ranks
Returns
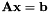True if $\mathbf{A}\mathbf{x} = \mathbf{b}$ has a solution.

Here is an example with $\mathbf{A} = \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 1 & 1& 0 & 0\end{array}\right]$ and $\mathbf{b} = \left[\begin{array}{c}0\\0\\0\end{array}\right]$ (feasible) or $\mathbf{b} = \left[\begin{array}{c}0\\0\\1\end{array}\right]$ (not feasible).

#include <visp3/core/vpLinProg.h>
int main()
{
vpMatrix A(3,4);
vpColVector b(3);
A[0][0] = A[1][1] = 1;
A[2][0] = A[2][1] = 1;
// b[2] = 1; // uncomment to make it unfeasible
if(vpLinProg::rowReduction(A, b))
std::cout << A << std::endl; // A is now 2x4
else
std::cout << "Ax = b not feasible\n";
}

Definition at line 264 of file vpLinProg.cpp.

References allClose(), vpMatrix::extract(), vpArray2D< Type >::getCols(), vpArray2D< Type >::getRows(), vpMatrix::inverseTriangular(), vpMatrix::qrPivot(), vpMatrix::stack(), and vpMatrix::transpose().

Referenced by simplex().

bool vpLinProg::simplex ( const vpColVector &  c,
vpMatrix  A,
vpColVector  b,
vpColVector &  x,
const double &  tol = 1e-6 
)
static

Solves a Linear Program under simplex canonical form

$\begin{array}{lll} \mathbf{x} = & \arg\min & \mathbf{c}^T\mathbf{x}\\ & \text{s.t.}& \mathbf{A}\mathbf{x} = \mathbf{b}\\ & \text{s.t.}& \mathbf{x} \geq 0 \end{array} $

Parameters
c: cost vector (dimension n)
A: equality matrix (dimension m x n)
b: equality vector (dimension m)
x: in: feasible point if any, out: solution (dimension n)
tol: tolerance to test the ranks
Returns
True if the solution was found.
Warning
This function is only available if C++11 is activated during compilation. Configure ViSP using cmake -DUSE_CPP11=ON.

Here is an example:

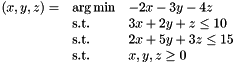
$\begin{array}{lll} (x,y,z) = & \arg\min & -2x -3y -4z\\ & \text{s.t.}& 3x + 2y + z \leq 10\\ & \text{s.t.}& 2x + 5y + 3z \leq 15\\ & \text{s.t.}& x, y, z \geq 0\end{array}$

That can be re-written as:

$\begin{array}{lll} (x,y,z), (s_1, s_2) = & \arg\min & -2x -3y -4z\\ & \text{s.t.}& 3x + 2y + z + s_1 = 10\\ & \text{s.t.}& 2x + 5y + 3z + s_2 = 15\\ & \text{s.t.}& x, y, z, s_1, s_2 \geq 0\end{array}$

#include <visp3/core/vpLinProg.h>
int main()
{
vpColVector c(5), x;
vpMatrix A(2, 5);
vpColVector b(2);
c[0] = -2; c[1] = -3; c[2] = -4;
A[0][0] = 3; A[0][1] = 2; A[0][2] = 1; b[0] = 10;
A[1][0] = 2; A[1][1] = 5; A[1][2] = 3; b[1] = 15;
A[0][3] = A[1][4] = 1;
if(vpLinProg::simplex(c, A, b, x))
{
std::cout << "x: " << x.t().extract(0,3) << std::endl;
std::cout << "cost: " << c.t()*x << std::endl;
}
}
See also
solveLP

Definition at line 563 of file vpLinProg.cpp.

References allClose(), allGreater(), allLesser(), vpColVector::extract(), vpMatrix::getCol(), vpArray2D< Type >::getRows(), vpMatrix::inverseByQR(), vpColVector::resize(), rowReduction(), vpColVector::t(), and vpMatrix::t().

Referenced by solveLP(), and vpQuadProg::solveQPi().

bool vpLinProg::solveLP ( const vpColVector &  c,
vpMatrix  A,
vpColVector  b,
const vpMatrix &  C,
const vpColVector &  d,
vpColVector &  x,
std::vector< BoundedIndex >  l = {},
std::vector< BoundedIndex >  u = {},
const double &  tol = 1e-6 
)
static

Solves a Linear Program under various constraints

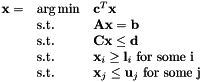
$\begin{array}{lll} \mathbf{x} = & \arg\min & \mathbf{c}^T\mathbf{x}\\ & \text{s.t.}& \mathbf{A}\mathbf{x} = \mathbf{b}\\ & \text{s.t.}& \mathbf{C}\mathbf{x} \leq \mathbf{d}\\ & \text{s.t.}& \mathbf{x}_i \geq \mathbf{l}_i \text{~for some i}\\ & \text{s.t.}& \mathbf{x}_j \leq \mathbf{u}_j \text{~for some j} \end{array} $

Parameters
c: cost vector (dimension n)
A: equality matrix (dimension m x n)
b: equality vector (dimension m)
C: inequality matrix (dimension p x n)
d: inequality vector (dimension p)
x: in: feasible point if any, out: solution (dimension n)
l: lower bounds (if any)
u: upper bounds (if any)
tol: tolerance to test the ranks
Returns
True if the solution was found.

Lower and upper bounds may be passed as a list of (index, bound) with C++11's braced initialization.

Warning
This function is only available if C++11 is activated during compilation. Configure ViSP using cmake -DUSE_CPP11=ON.

Here is an example:

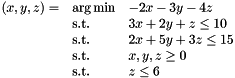
$\begin{array}{lll} (x,y,z) = & \arg\min & -2x -3y -4z\\ & \text{s.t.}& 3x + 2y + z \leq 10\\ & \text{s.t.}& 2x + 5y + 3z \leq 15\\ & \text{s.t.}& x, y, z \geq 0\\ & \text{s.t.}& z \leq 6\end{array}$

#include <visp3/core/vpLinProg.h>
int main()
{
vpColVector c(3), x;
vpMatrix C(2, 3);
vpColVector d(2);
c[0] = -2; c[1] = -3; c[2] = -4;
C[0][0] = 3; C[0][1] = 2; C[0][2] = 1; d[0] = 10;
C[1][0] = 2; C[1][1] = 5; C[1][2] = 3; d[1] = 15;
if(vpLinProg::solveLP(c, vpMatrix(0,0), vpColVector(0), C, d, x,
{{0,0},{1,0},{2,0}},
{{2,6}}))
{
std::cout << "x: " << x.t() << std::endl;
std::cout << "cost: " << c.t()*x << std::endl;
}
}
See also
BoundedIndex

Definition at line 348 of file vpLinProg.cpp.

References allClose(), allLesser(), colReduction(), vpColVector::extract(), vpMatrix::eye(), vpArray2D< Type >::getCols(), vpMatrix::getRow(), vpArray2D< Type >::getRows(), vpArray2D< Type >::resize(), vpColVector::resize(), simplex(), and vpMatrix::transpose().