 |
Visual Servoing Platform
version 3.0.1
|
|
Visual Servoing Platform
version 3.0.1
|
The aim of all vision-based control schemes is to minimize an error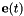 
, which is typically defined by ![${\bf e}(t) = {\bf s}[{\bf m}(t), {\bf a}]-{\bf s}^*$](form_1146.png)
.
Traditional image-based control schemes use the image-plane coordinates of a set of points to define the set of visual features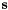 
. The image measurements 
are usually the pixel coordinates of the set of image points (but this is not the only possible choice), and the camera intrinsic parameters 
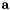are used to go from image measurements expressed in pixels to the features.
For a 3D point with coordinates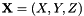 
in the camera frame, which projects in the image as a 2D point with coordinates 
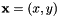we have:
![\[ \left\{\begin{array}{l} x = X/Z = (u - u_0)/p_x\\ y = Y/Z = (v - v_0)/p_y \end{array}\right. \]](form_1150.png)
where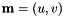 
gives the coordinates of the image point expressed in pixel units, and 
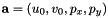is the set of camera intrinsic parameters: 
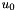and 
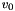are the coordinates of the principal point, while 
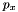and 
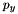are the ratio between the focal length and the size of a pixel.
Let the spatial velocity of the camera be denoted by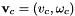 
, with 
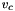the instantaneous linear velocity of the origin of the camera frame and 
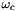the instantaneous angular velocity of the camera frame. The relationship between 
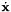, the time variation of the feature 
, and the camera velocity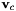 
is given by
![\[ \dot{\bf s} = {\bf L_x} {\bf v}_c\]](form_1163.png)
where the interaction matrix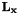 
is given by
![\[ {\bf L_x} = \left[\begin{array}{cccccc} -1/Z & 0 & x/Z & xy & -(1+x^2) & y \\ 0 & -1/Z & y/Z & 1+y^2 & -xy & -x \end{array}\right]\]](form_1165.png)
Considering 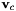as the input to the robot controller, and if we would like for instance to try to ensure an exponential decoupled decrease of the error, we obtain
![\[ {\bf v}_c = -\lambda {\bf L}_{\bf x}^{+} {\bf e} \]](form_1166.png)
Note that all the material (source code and image) described in this tutorial is part of ViSP source code and could be downloaded using the following command:
The following example available in tutorial-ibvs-4pts.cpp shows how to use ViSP to implement an IBVS simulation using 4 points as visual features.
Now we give a line by line description of the source:
Include a kind of common header for all the classes that implement visual features, especially in our case vpFeaturePoint that will allow us to handle described in the Introduction.
Include the header of the vpServo class that implements the control law
described in the Introduction.
Include the header of the vpSimulatorCamera class that allows to simulate a 6 dof free flying camera.
Then in the main() function, we define the desired and initial position of the camera as two homogeneous matrices; cdMo refers to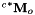 
and cMo to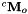 
.
Then we define four 3D points that represent the corners of a 20cm by 20cm square.
The instantiation of the visual servo task is done with the next lines. We initialize the task as an eye in hand visual servo. Resulting velocities computed by the controller are those that should be applied in the camera frame: 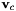. The interaction matrix will be computed from the current visual features. Thus they need to be updated at each iteration of the control loop. Finally, the constant gain 
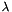is set to 0.5.
It is now time to define four visual features as points in the image-plane. To this end we instantiate the vpFeaturePoint class. The current point feature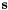 
is implemented in p[i]. The desired point feature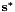 
is implemented in pd[i].
Each feature is obtained by computing the position of the 3D points in the corresponding camera frame, and then by applying the perspective projection. Once current and desired features are created, they are added to the visual servo task.
For the simulation we need first to create two homogeneous transformations wMc and wMo, respectively to define the position of the camera, and the position of the object in the world frame.
Secondly. we create an instance of our free flying camera. Here we also specify the sampling time to 0.040 seconds. When a velocity is applied to the camera, this time will be used by the exponential map to determine the next position of the camera.
Finally, from the initial position wMc of the camera and the position of the object previously fixed in the camera frame cMo, we compute the position of the object in the world frame wMo. Since in our simulation the object is static, wMo will remain unchanged.
Now we can enter in the visual servo loop. When a velocity is applied to our free flying camera, the position of the camera frame wMc will evolve wrt the world frame. From this position we compute the position of object in the new camera frame.
The current visual features are then updated by projecting the 3D points in the image-plane associated to the new camera location cMo.
Finally, the velocity skew 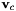is computed.
This 6-dimension velocity vector is then applied to the camera.
Before exiting the program, we free all the memory by killing the task.
The next Tutorial: Real-time curves plotter tool shows how to modify the previous example to plot some curves that illustrate the visual servo behavior.
The previous IBVS simulation can be modified easily to introduce a basic internal and external camera viewer. This is implemented in tutorial-ibvs-4pts-display.cpp and given below:
The result of this program is visible in the next videos. The first one shows the internal camera view with the straight line trajectory of each point in the image. The second one provides an external view that shows the 3D camera trajectory to reach the desired position.
We explain now the new lines that were introduced.
First, we add the headers of the classes that are used to introduce the viewers and some display functionality. vpProjectionDisplay is the class that allows to handle the external view from a given camera position, while vpServoDisplay allows to display in overlay the position of the current and desired features in the internal camera view.
Secondly, we introduce the function display_trajectory() that allows to display the trajectory of the current features in the image. From the 3D coordinates of the points given in the object frame, we compute their respective position in the camera frame, then we apply the perspective projection before retrieving their positions in sub-pixels in the image thanks to the camera parameters. The successive sub-pixel positions are stored in a vector named traj and displayed as a green trajectory.
We enter then in the main() where we create two images that will be displayed in a window. The first images Iint is dedicated to the internal camera view. It shows the content of the images seen by the simulated camera. The second image Iext correspond the images seen by an external camera that observes the simulated camera.
We create an instance of the vpProjectionDisplay class. This class is only available if at least one of the display (X11, GDI, OpenCV, GTK, D3D9) is installed. That is why we use VISP_HAVE_DISPLAY macro. We then insert the points used to define the target. Later, the 3D coordinates of these points defined in the object frame will be used and projected in Iext.
We initialize the intrinsic camera parameters that are used in display_trajectory() to determine the positions in pixels in the image of the visual features.
We also set the position of the external camera that will observe the evolution of the simulated camera during the servo.
Finally, at each iteration of the servo loop we update the viewers:
The IBVS simulation presented section Basic IBVS simulation can also be modified to introduce a wireframe internal and external camera viewer. This is implemented in tutorial-ibvs-4pts-wireframe-camera.cpp and given below:
The result of this program is visible in the next videos. The first one shows the internal wireframe camera view with the straight line trajectory of each point in the image. The second one provides an external wireframe view that shows the 3D camera trajectory to reach the desired position.
We explain now the new lines that were introduced.
First we include the header of the wireframe simulator.
Then in the main(), we create an instance of the simulator. First we initialize the object in the scene. We recall that the target is a 20cm by 20cm square. This is exactly an object handled by the simulator and defined as a vpWireFrameSimulator::PLATE. By vpWireFrameSimulator::D_STANDARD we indicate that the object displayed at the desired position is also a PLATE. Secondly we initialize the camera position wrt to the object using cMo, and also the desired camera position, the one the camera has to reach at the end of the servo, using cdMo. Next we initialize the position of a static external camera that will observe the simulated camera during the servoing using cextMo. All these poses are define wrt the object frame. Finally, we set the intrinsic camera parameters used for the internal and external viewers.
At each iteration of the servo loop, we update the wireframe simulator with the new camera position.
Then we update the drawings in the internal and external viewers associated to their respective images.
Note here that the same kind of simulation could be achieved on a Viper arm or a gantry robot. The programs that does the simulation are provided in tutorial-ibvs-4pts-wireframe-robot-viper.cpp and in tutorial-ibvs-4pts-wireframe-robot-afma6.cpp.
The next video illustrate the behavior of the same IBVS implemented in tutorial-ibvs-4pts-wireframe-robot-viper.cpp on a Viper arm.
The IBVS simulation presented section Basic IBVS simulation can be modified to introduce an image processing that allows to track the point features using a blob tracker. This is implemented in tutorial-ibvs-4pts-image-tracking.cpp. The code is given below:
The result of this program is visible in the next video.
We explain now the new lines that were introduced.
First we create a white image in which the target will be projected prior to the image processing.
Since we will have to convert pixel coordinates to visual features expressed in meter, we need to initialize intrinsic camera parameters.
To retrieve the simulated image that depends on the simulated camera position we create an instance of a virtual grabber. Its goal is to project the image of the target ./target_square.pgm to a given camera position cMo, and then to retrieve the corresponding image I. Note here that the cog of the blobs in the .pgm file define a 20cm by 20cm square.
The current visual features are computed using a vpDot2 blob tracker. Once four trackers are instantiated, we are waiting for a mouse click in each blob to initialize the tracker. Then we compute the current visual features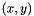 
from the camera parameters and the cog position of each blob.
In the visual servo loop, at each iteration we get a new image of the target.
We track each blob and update the values of the current visual features as previously.
As described in the Introduction, since the interaction matrix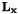 
depends on 
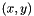but also on 
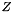the depth of the feature, we need to update 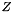. This is done by projecting each 3D point of the target in the camera frame using:
You are now ready to see the Tutorial: Visual servo simulation on a pioneer-like unicycle robot and Tutorial: How to boost your visual servo control law.
1.8.6 
