 |
Visual Servoing Platform
version 3.0.1
|
 |
Visual Servoing Platform
version 3.0.1
|
#include <visp3/core/vpLinearKalmanFilterInstantiation.h>
 Inheritance diagram for vpLinearKalmanFilterInstantiation:
Inheritance diagram for vpLinearKalmanFilterInstantiation:Public Types | |
| enum | vpStateModel { stateConstVel_MeasurePos, stateConstVelWithColoredNoise_MeasureVel, stateConstAccWithColoredNoise_MeasureVel, unknown } |
Public Member Functions | |
| vpLinearKalmanFilterInstantiation () | |
| virtual | ~vpLinearKalmanFilterInstantiation () |
| vpStateModel | getStateModel () |
| void | filter (vpColVector &z) |
| void | setNumberOfSignal (unsigned int n_signal) |
| void | init (unsigned int size_state, unsigned int size_measure, unsigned int n_signal) |
| void | prediction () |
| void | filtering (const vpColVector &z) |
| unsigned int | getStateSize () |
| unsigned int | getMeasureSize () |
| unsigned int | getNumberOfSignal () |
| long | getIteration () |
| void | verbose (bool on) |
Generic linear filter initializer | |
| void | setStateModel (vpStateModel model) |
| void | initFilter (unsigned int nsignal, vpColVector &sigma_state, vpColVector &sigma_measure, double rho, double dt) |
Linear filter initializer with constant velocity models | |
| void | initStateConstVel_MeasurePos (unsigned int nsignal, vpColVector &sigma_state, vpColVector &sigma_measure, double dt) |
| void | initStateConstVelWithColoredNoise_MeasureVel (unsigned int nsignal, vpColVector &sigma_state, vpColVector &sigma_measure, double rho) |
Linear filter initializer with constant acceleration models | |
| void | initStateConstAccWithColoredNoise_MeasureVel (unsigned int nsignal, vpColVector &sigma_state, vpColVector &sigma_measure, double rho, double dt) |
Public Attributes | |
| vpColVector | Xest |
| vpColVector | Xpre |
| vpMatrix | F |
| vpMatrix | H |
| vpMatrix | R |
| vpMatrix | Q |
| double | dt |
| vpMatrix | Ppre |
| vpMatrix | Pest |
Protected Attributes | |
| vpStateModel | model |
| long | iter |
| unsigned int | size_state |
| unsigned int | size_measure |
| unsigned int | nsignal |
| bool | verbose_mode |
| vpMatrix | W |
| vpMatrix | I |
This class provides an implementation of some specific linear Kalman filters.
Definition at line 56 of file vpLinearKalmanFilterInstantiation.h.
Selector used to set the Kalman filter state model.
| Enumerator | |
|---|---|
| stateConstVel_MeasurePos |
Consider the state as a constant velocity model with white noise. Measures available are the succesive positions of the target. To know more about this state model, see initStateConstVel_MeasurePos(). |
| stateConstVelWithColoredNoise_MeasureVel |
Consider the state as a constant velocity model with colored noise measurements as acceleration terms. Measured available are the velocities of the target. To know more about this state model, see initStateConstVelWithColoredNoise_MeasureVel(). |
| stateConstAccWithColoredNoise_MeasureVel |
Consider the state as a constant acceleration model with colored noise measurements as acceleration terms. Measured available are the velocities of the target. To know more about this state model, see initStateConstAccWithColoredNoise_MeasureVel(). |
| unknown |
Used to indicate that the state model is not initialized. |
Definition at line 62 of file vpLinearKalmanFilterInstantiation.h.
|
inline |
Default linear Kalman filter.
By default the state model is unknown and set to vpLinearKalmanFilterInstantiation::unknown.
Definition at line 88 of file vpLinearKalmanFilterInstantiation.h.
|
inlinevirtual |
Destructor that does nothng.
Definition at line 93 of file vpLinearKalmanFilterInstantiation.h.
| void vpLinearKalmanFilterInstantiation::filter | ( | vpColVector & | z | ) |
Do the filtering and prediction of the measure signal.
| z | : Measures 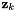 used to initialise the filter. The dimension of this vector is equal to the number of signal to filter (given by getNumberOfSignal()) multiplied by the size of the measure vector (given by getMeasureSize()) . used to initialise the filter. The dimension of this vector is equal to the number of signal to filter (given by getNumberOfSignal()) multiplied by the size of the measure vector (given by getMeasureSize()) . |
| vpException::notInitialized | : If the filter is not initialized. To initialize the filter see initFilter(). |
Definition at line 806 of file vpLinearKalmanFilterInstantiation.cpp.
References vpKalmanFilter::dt, vpKalmanFilter::filtering(), vpKalmanFilter::iter, model, vpException::notInitialized, vpKalmanFilter::nsignal, vpKalmanFilter::prediction(), vpKalmanFilter::size_measure, vpKalmanFilter::size_state, stateConstAccWithColoredNoise_MeasureVel, stateConstVel_MeasurePos, stateConstVelWithColoredNoise_MeasureVel, unknown, vpERROR_TRACE, and vpKalmanFilter::Xest.
|
inherited |
Update the Kalman filter by applying the filtering equations and increment the filter iteration (vpKalmanFilter::iter).
| z | : Measure (or observation) 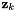 provided at iteration provided at iteration 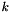 . . |
The filtering equation is given by:
![\[ {\bf x}_{k \mid k} = {\bf x}_{k \mid k-1} + {\bf W}_k \left[ {\bf z}_k - {\bf H} {\bf x}_{k \mid k-1} \right] \]](form_296.png)
where 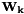 is the filter gain computed using the formula:
is the filter gain computed using the formula:
![\[ {\bf W_k} = {\bf P}_{k \mid k-1} {\bf H}^T \left[ {\bf H P}_{k \mid k-1} {\bf H}^T + {\bf R}_k \right]^{-1} \]](form_298.png)
and where the updated covariance of the state is given by
![\[ {\bf P}_{k \mid k} = \left({\bf I} - {\bf W}_k {\bf H} \right) {\bf P}_{k \mid k-1} \]](form_299.png)
or in a symetric form
![\[ {\bf P}_{k \mid k} = {\bf P}_{k \mid k-1} - {\bf W}_k {\bf S}_k {\bf W}^T_k \]](form_300.png)
with
![\[ {\bf S}_k = {\bf H P}_{k \mid k-1} {\bf H}^T + {\bf R}_k \]](form_301.png)
Definition at line 212 of file vpKalmanFilter.cpp.
References vpKalmanFilter::H, vpMatrix::inverseByLU(), vpKalmanFilter::iter, vpKalmanFilter::Pest, vpKalmanFilter::Ppre, vpKalmanFilter::R, vpMatrix::t(), vpKalmanFilter::verbose_mode, vpKalmanFilter::W, vpKalmanFilter::Xest, and vpKalmanFilter::Xpre.
Referenced by filter().
|
inlineinherited |
Return the iteration number.
Definition at line 159 of file vpKalmanFilter.h.
|
inlineinherited |
Return the size of the measure vector 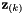 for one signal.
for one signal.
Definition at line 151 of file vpKalmanFilter.h.
|
inlineinherited |
Return the number of signal to filter.
Definition at line 155 of file vpKalmanFilter.h.
|
inline |
Return the current state model.
Definition at line 97 of file vpLinearKalmanFilterInstantiation.h.
|
inlineinherited |
Return the size of the state vector 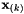 for one signal.
for one signal.
Definition at line 147 of file vpKalmanFilter.h.
|
inherited |
Initialize the Kalman filter.
| size_state_vector | : Size of the state vector 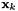 for one signal. for one signal. |
| size_measure_vector | : Size of the measure vector 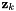 for one signal. for one signal. |
| n_signal | : Number of signal to filter. |
Definition at line 61 of file vpKalmanFilter.cpp.
References vpKalmanFilter::dt, vpKalmanFilter::F, vpKalmanFilter::H, vpKalmanFilter::I, vpKalmanFilter::iter, vpKalmanFilter::nsignal, vpKalmanFilter::Pest, vpKalmanFilter::Q, vpKalmanFilter::R, vpArray2D< Type >::resize(), vpColVector::resize(), vpKalmanFilter::size_measure, vpKalmanFilter::size_state, vpKalmanFilter::Xest, and vpKalmanFilter::Xpre.
Referenced by initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), and vpKalmanFilter::vpKalmanFilter().
| void vpLinearKalmanFilterInstantiation::initFilter | ( | unsigned int | n_signal, |
| vpColVector & | sigma_state, | ||
| vpColVector & | sigma_measure, | ||
| double | rho, | ||
| double | delta_t | ||
| ) |
Initialize the Kalman filter material depending on the selected state model set with setStateModel(). This function is provided as a wrapper over all the other initializer functions like initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), initStateConstAccWithColoredNoise_MeasureVel().
| n_signal | : Number of signal to filter. |
| sigma_state | : Vector that contains the variance of the state noise. The dimension of this vector is equal to the state vector 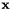 size multiplied by the number of signal to filter. Values are used to initialize the size multiplied by the number of signal to filter. Values are used to initialize the 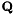 state covariance matrix. state covariance matrix. |
| sigma_measure | : Vector that contains the variance of the measurement noise. The dimension of this vector is equal to the measure vector 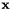 size multiplied by the number of signal to filter. Values are used to initialize the size multiplied by the number of signal to filter. Values are used to initialize the 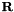 measure covariance matrix. measure covariance matrix. |
| rho | : Degree of correlation between successive accelerations. Values are in [0:1[. |
| delta_t | : Sampling time 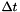 expressed is second. Depending on the filter modelization, this value may not be used. This is for example the case for the vpLinearKalmanFilterInstantiation::stateConstVelWithColoredNoise_MeasureVel model implemented in initStateConstVelWithColoredNoise_MeasureVel(). expressed is second. Depending on the filter modelization, this value may not be used. This is for example the case for the vpLinearKalmanFilterInstantiation::stateConstVelWithColoredNoise_MeasureVel model implemented in initStateConstVelWithColoredNoise_MeasureVel(). |
| vpException::badValue | : Bad rho value wich is not in [0:1[. |
| vpException::notInitialized | : If the state model is not initialized. To initialize it you need to call setStateModel(). |
The example below shows how to initialize the filter for a one dimensional signal.
The example below shows a more complete example to filter a two dimensional target trajectory with an estimation of the target velocities from velocity measures.
Definition at line 174 of file vpLinearKalmanFilterInstantiation.cpp.
References initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), model, vpException::notInitialized, stateConstAccWithColoredNoise_MeasureVel, stateConstVel_MeasurePos, stateConstVelWithColoredNoise_MeasureVel, unknown, and vpERROR_TRACE.
| void vpLinearKalmanFilterInstantiation::initStateConstAccWithColoredNoise_MeasureVel | ( | unsigned int | n_signal, |
| vpColVector & | sigma_state, | ||
| vpColVector & | sigma_measure, | ||
| double | rho, | ||
| double | delta_t | ||
| ) |
Modelisation of a constant acceleration state model with colored noise. The measure is assumed to be the velocity of the target.
This state model assume that there is some memory associated with noise measurements as acceleration terms. They can be represented as remaining correlated (or colored) over succesive time intervals, leading to the following state model:
![\[ \left\{ \begin{array}{rll} x_{(k+1)} & = x_{(k)} + \Delta t \; \dot{x}_{(k)} + \nu_{(k)} &\\ \nu_{(k+1)}& = \rho \nu_{(k)} &+w_{1(k)} \\ \dot{x}_{(k+1)} & = \dot{x}_{(k)} &+w_{2(k)}\\ \end{array} \right. \]](form_329.png)
The terms 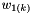 and
and 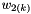 account for deviations from the assumed constant acceleration trajectory. They are assumed zero-mean, white, mutually uncorrelated, stationary random variable with variance
account for deviations from the assumed constant acceleration trajectory. They are assumed zero-mean, white, mutually uncorrelated, stationary random variable with variance 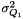 and
and 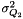 . The term
. The term 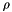 is the degree of correlation between successive accelerations. Values can range from 0 to 1.
is the degree of correlation between successive accelerations. Values can range from 0 to 1.
We recall that the recursive state evolution equation is given by
![\[ {\bf x}_k= {\bf F}_{k-1} {\bf x}_{k-1} + {\bf w}_{k-1} \\ \]](form_106.png)
From this state model, the transition matrix 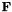 and the state covariance matrix
and the state covariance matrix 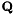 are given by:
are given by:
![\[ {\bf F} = \left[ \begin{array}{ccc} 1 & 1 & \Delta t\\ 0 & \rho & 0 \\ 0 & 0 & 1 \end{array} \right] \]](form_332.png)
and
![\[ {\bf Q} = \left[ \begin{array}{ccc} 0 & 0 & 0\\ 0 & \sigma^2_{Q_1} & 0\\ 0 & 0& \sigma^2_{Q_2} \\ \end{array} \right] \]](form_333.png)
The measurement model is given by:
![\[ z_{(k)} = {\bf H} {\bf x}_{(k)} + r_{(k)} \]](form_322.png)
where ![${\bf H} = [1 \; 0 \; 0]$](form_323.png) ,
, 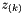 is the measure of the velocity and
is the measure of the velocity and 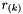 is the measurement noise, assumed zero-mean, white mutually uncorrelated stationary random variables with variance
is the measurement noise, assumed zero-mean, white mutually uncorrelated stationary random variables with variance 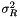 , giving the covariance matrix:
, giving the covariance matrix:
![\[ {\bf R} = \left[\sigma^2_R\right] \]](form_326.png)
The initial value of the state vector is set to:
![\[ {\bf x_{(0)}} = \left[ \begin{array}{c} z_{(0)}\\ 0 \\ 0 \end{array} \right] \]](form_334.png)
The initial value 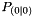 of the prediction covariance matrix is given by:
of the prediction covariance matrix is given by:
![\[ {\bf P_{(0|0)}} = \left[ \begin{array}{ccc} \sigma^2_R & 0 & \sigma^2_R / \Delta t\\ 0 & \sigma^2_{Q_1}/(1-\rho^2) & -\rho \sigma^2_{Q_1} / (1-\rho^2)\Delta t \\ \sigma^2_R / \Delta t & -\rho \sigma^2_{Q_1} / (1-\rho^2)\Delta t & (2\sigma^2_R +\sigma^2_{Q_1}/(1-\rho^2) )/\Delta t^2 \end{array} \right] \]](form_335.png)
| n_signal | : Number of signal to filter. |
| sigma_state | : Vector that fix the variance of the state covariance matrix ![$[0 \; \sigma^2_{Q_1} \; \sigma^2_{Q_2}]^T$](form_336.png) . The dimension of this vector is 3 multiplied by the number of signal to filter. . The dimension of this vector is 3 multiplied by the number of signal to filter. |
| sigma_measure | : Variance 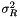 of the measurement noise. The dimension of this vector is equal to the number of signal to filter. of the measurement noise. The dimension of this vector is equal to the number of signal to filter. |
| rho | : Degree of correlation between successive accelerations. Values are in [0:1[. |
| delta_t | : Sampling time 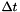 expressed is second. expressed is second. |
| vpException::badValue | : Bad rho value wich is not in [0:1[. |
The example below shows how to filter a two dimensional target trajectory with an estimation of the target velocity from velocity measures.
Definition at line 728 of file vpLinearKalmanFilterInstantiation.cpp.
References vpException::badValue, vpKalmanFilter::dt, vpKalmanFilter::F, vpKalmanFilter::H, vpKalmanFilter::init(), vpKalmanFilter::iter, vpKalmanFilter::nsignal, vpKalmanFilter::Pest, vpKalmanFilter::Q, vpKalmanFilter::R, setStateModel(), vpKalmanFilter::size_measure, vpKalmanFilter::size_state, stateConstAccWithColoredNoise_MeasureVel, vpERROR_TRACE, and vpKalmanFilter::Xest.
Referenced by initFilter().
| void vpLinearKalmanFilterInstantiation::initStateConstVel_MeasurePos | ( | unsigned int | n_signal, |
| vpColVector & | sigma_state, | ||
| vpColVector & | sigma_measure, | ||
| double | delta_t | ||
| ) |
Modelisation of a constant speed state model with white noise. The measure is assumed to be the position of the target.
The considered state model is the following
![\[ \left\{ \begin{array}{rlrl} x_{(k+1)} & = x_{(k)} & + \Delta t \; {\dot{x}}_{(k)} & + {w_1}_{(k)} \\ {\dot{x}}_{(k+1)} & = & {\dot{x}}_{(k)} &+{w_2}_{(k)} \end{array} \right. \]](form_303.png)
The terms 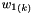 and
and 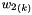 account for deviations from the assumed constant velocity trajectory. They are assumed zero-mean, white, mutually uncorrelated, stationary random variable with variance
account for deviations from the assumed constant velocity trajectory. They are assumed zero-mean, white, mutually uncorrelated, stationary random variable with variance 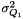 and
and 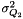 .
.
We recall that the recursive state evolution equation is given by
![\[ {\bf x}_k= {\bf F}_{k-1} {\bf x}_{k-1} + {\bf w}_{k-1} \\ \]](form_106.png)
From this state model, the transition matrix 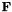 and the state covariance matrix
and the state covariance matrix 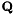 are given by:
are given by:
![\[ {\bf F} = \left[ \begin{array}{cc} 1 & \Delta t\\ 0 & 1 \end{array} \right] \]](form_308.png)
and
![\[ {\bf Q} = \sigma^2_Q \left[ \begin{array}{cc} \frac{1}{3}\Delta t^3 & \frac{1}{2}\Delta t^2\\ \frac{1}{2}\Delta t^2 & \Delta t \end{array} \right] \]](form_309.png)
The initial value of the state vector at iteration 0 is set to:
![\[ {\bf x_{(0)}} = \left[ \begin{array}{c} z_{(0)}\\ 0 \end{array} \right] \]](form_310.png)
The value at iteration 1 is set to:
![\[ {\bf x_{(1)}} = \left[ \begin{array}{c} z_{(1)}\\ (z_{(1)} - z_{(0)})/ \Delta t \end{array} \right] \]](form_311.png)
The initial value 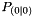 of the prediction covariance matrix is given by:
of the prediction covariance matrix is given by:
![\[ {\bf P_{(0|0)}} = \left[ \begin{array}{cc} \sigma^2_R & \frac{\sigma^2_R}{2 \Delta t}\\ \frac{\sigma^2_R}{2 \Delta t} & \frac{2}{3}\sigma^2_Q \Delta t + \frac{\sigma^2_R}{2 \Delta t^2} \end{array} \right] \]](form_313.png)
| n_signal | : Number of signal to filter. |
| sigma_state | : Vector that fix the variance of the state covariance matrix ![$[\sigma^2_Q \; 0]^T$](form_314.png) . The dimension of this vector is 2 multiplied by the number of signal to filter. . The dimension of this vector is 2 multiplied by the number of signal to filter. |
| sigma_measure | : Variance 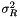 of the measurement noise. The dimension of this vector is equal to the number of signal to filter. of the measurement noise. The dimension of this vector is equal to the number of signal to filter. |
| delta_t | : Sampling time 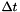 expressed is second. expressed is second. |
Definition at line 296 of file vpLinearKalmanFilterInstantiation.cpp.
References vpKalmanFilter::dt, vpKalmanFilter::F, vpKalmanFilter::H, vpKalmanFilter::init(), vpKalmanFilter::iter, vpKalmanFilter::Pest, vpKalmanFilter::Q, vpKalmanFilter::R, setStateModel(), vpKalmanFilter::size_measure, vpKalmanFilter::size_state, stateConstVel_MeasurePos, and vpKalmanFilter::Xest.
Referenced by initFilter().
| void vpLinearKalmanFilterInstantiation::initStateConstVelWithColoredNoise_MeasureVel | ( | unsigned int | n_signal, |
| vpColVector & | sigma_state, | ||
| vpColVector & | sigma_measure, | ||
| double | rho | ||
| ) |
Modelisation of a constant speed state model with colored noise. The measure is assumed to be the velocity of the target.
This state model assume that there is some memory associated with noise measurements as acceleration terms. They can be represented as remaining correlated (or colored) over succesive time intervals, leading to the following state model:
![\[ \left\{ \begin{array}{rll} x_{(k+1)} & = x_{(k)} + \nu_{(k)} &\\ \nu_{(k+1)}& = \rho \nu_{(k)} &+w_{(k)} \end{array} \right. \]](form_316.png)
The term 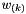 account for deviations from the assumed constant velocity trajectory. It is assumed zero-mean, white, mutually uncorrelated, stationary random variable with variance
account for deviations from the assumed constant velocity trajectory. It is assumed zero-mean, white, mutually uncorrelated, stationary random variable with variance 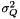 . The term
. The term 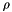 is the degree of correlation between successive accelerations. Values can range from 0 to 1.
is the degree of correlation between successive accelerations. Values can range from 0 to 1.
We recall that the recursive state evolution equation is given by
![\[ {\bf x}_k= {\bf F}_{k-1} {\bf x}_{k-1} + {\bf w}_{k-1} \\ \]](form_106.png)
From this state model, the transition matrix 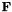 and the state covariance matrix
and the state covariance matrix 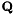 are given by:
are given by:
![\[ {\bf F} = \left[ \begin{array}{cc} 1 & 1\\ 0 & \rho \end{array} \right] \]](form_320.png)
and
![\[ {\bf Q} = \left[ \begin{array}{cc} 0 & 0\\ 0 & \sigma^2_Q \end{array} \right] \]](form_321.png)
The measurement model is given by:
![\[ z_{(k)} = {\bf H} {\bf x}_{(k)} + r_{(k)} \]](form_322.png)
where ![${\bf H} = [1 \; 0 \; 0]$](form_323.png) ,
, 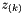 is the measure of the velocity and
is the measure of the velocity and 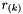 is the measurement noise, assumed zero-mean, white mutually uncorrelated stationary random variables with variance
is the measurement noise, assumed zero-mean, white mutually uncorrelated stationary random variables with variance 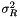 , giving the covariance matrix:
, giving the covariance matrix:
![\[ {\bf R} = \left[\sigma^2_R\right] \]](form_326.png)
The initial value of the state vector is set to:
![\[ {\bf x_{(0)}} = \left[ \begin{array}{c} z_{(0)}\\ 0 \end{array} \right] \]](form_310.png)
The initial value 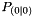 of the prediction covariance matrix is given by:
of the prediction covariance matrix is given by:
![\[ {\bf P_{(0|0)}} = \left[ \begin{array}{cc} \sigma^2_R & 0\\ 0 & \sigma^2_Q/(1-\rho^2) \end{array} \right] \]](form_327.png)
| n_signal | : Number of signal to filter. |
| sigma_state | : Vector that fix the variance of the state covariance matrix ![$[0 \; \sigma^2_Q]^T$](form_328.png) . The dimension of this vector is 2 multiplied by the number of signal to filter. . The dimension of this vector is 2 multiplied by the number of signal to filter. |
| sigma_measure | : Variance 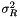 of the measurement noise. The dimension of this vector is equal to the number of signal to filter. of the measurement noise. The dimension of this vector is equal to the number of signal to filter. |
| rho | : Degree of correlation between successive accelerations. Values are in [0:1[. |
| vpException::badValue | : Bad rho value wich is not in [0:1[. |
The example below shows how to filter a two dimensional target trajectory with an estimation of the target velocity from velocity measures.
Definition at line 505 of file vpLinearKalmanFilterInstantiation.cpp.
References vpException::badValue, vpKalmanFilter::F, vpKalmanFilter::H, vpKalmanFilter::init(), vpKalmanFilter::iter, vpKalmanFilter::Pest, vpKalmanFilter::Q, vpKalmanFilter::R, setStateModel(), vpKalmanFilter::size_measure, vpKalmanFilter::size_state, stateConstVelWithColoredNoise_MeasureVel, vpERROR_TRACE, and vpKalmanFilter::Xest.
Referenced by initFilter().
|
inherited |
Update the Kalman filter by applying the prediction equations.
The predicted state is given by
![\[ {{\bf x}}_{k|k-1} = {\bf F}_{k-1} {\bf x}_{k-1\mid k-1} \]](form_295.png)
and the state prediction covariance by
![\[ {\bf P}_{k \mid k-1} = {\bf F}_{k-1} {\bf P}_{k-1 \mid k-1} {\bf F}^T_{k-1} + {\bf Q}_k \]](form_112.png)
Definition at line 144 of file vpKalmanFilter.cpp.
References vpKalmanFilter::F, vpArray2D< Type >::getRows(), vpKalmanFilter::nsignal, vpKalmanFilter::Pest, vpKalmanFilter::Ppre, vpKalmanFilter::Q, vpKalmanFilter::size_state, vpMatrix::t(), vpKalmanFilter::verbose_mode, vpKalmanFilter::Xest, and vpKalmanFilter::Xpre.
Referenced by filter().
|
inlineinherited |
Set the number of signal to filter.
Definition at line 135 of file vpKalmanFilter.h.
|
inline |
Set the Kalman state model. Depending on the state model, we set the state vector size and the measure vector size.
The example below shows how to use this method and then to get the size of the state and measure vectors.
Definition at line 156 of file vpLinearKalmanFilterInstantiation.h.
References model, vpKalmanFilter::size_measure, vpKalmanFilter::size_state, stateConstAccWithColoredNoise_MeasureVel, stateConstVel_MeasurePos, stateConstVelWithColoredNoise_MeasureVel, and unknown.
Referenced by initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), and initStateConstVelWithColoredNoise_MeasureVel().
|
inlineinherited |
Sets the verbose mode.
| on | : If true, activates the verbose mode which consists in printing the Kalman filter internal values. |
Definition at line 165 of file vpKalmanFilter.h.
|
inherited |
Sampling time 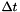 in second between two succesive iterations. Only used in some specific state models implemented in vpLinearKalmanFilterInstantiation.
in second between two succesive iterations. Only used in some specific state models implemented in vpLinearKalmanFilterInstantiation.
Definition at line 192 of file vpKalmanFilter.h.
Referenced by filter(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), and initStateConstVel_MeasurePos().
|
inherited |
Transition matrix 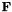 that describes the evolution of the state.
that describes the evolution of the state.
Definition at line 180 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), and vpKalmanFilter::prediction().
|
inherited |
Matrix 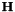 that describes the evolution of the measurements.
that describes the evolution of the measurements.
Definition at line 183 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::filtering(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), and initStateConstVelWithColoredNoise_MeasureVel().
|
protectedinherited |
Identity matrix 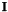 .
.
Definition at line 217 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::init().
|
protectedinherited |
Filter step or iteration. When set to zero, initialize the filter.
Definition at line 114 of file vpKalmanFilter.h.
Referenced by filter(), vpKalmanFilter::filtering(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), and initStateConstVelWithColoredNoise_MeasureVel().
|
protected |
Definition at line 132 of file vpLinearKalmanFilterInstantiation.h.
Referenced by filter(), initFilter(), and setStateModel().
|
protectedinherited |
Number of signal to filter.
Definition at line 121 of file vpKalmanFilter.h.
Referenced by filter(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), and vpKalmanFilter::prediction().
|
inherited |
The updated covariance of the state 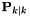 where
where 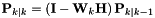 .
.
Definition at line 205 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::filtering(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), and vpKalmanFilter::prediction().
|
inherited |
The state prediction covariance 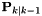 where
where 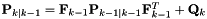 .
.
Definition at line 198 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::filtering(), and vpKalmanFilter::prediction().
|
inherited |
Process noise covariance matrix 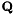 .
.
Definition at line 188 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), and vpKalmanFilter::prediction().
|
inherited |
Measurement noise covariance matrix 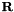 .
.
Definition at line 186 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::filtering(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), and initStateConstVelWithColoredNoise_MeasureVel().
|
protectedinherited |
Size of the measure vector 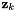 .
.
Definition at line 119 of file vpKalmanFilter.h.
Referenced by filter(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), and setStateModel().
|
protectedinherited |
Size of the state vector 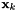 .
.
Definition at line 117 of file vpKalmanFilter.h.
Referenced by filter(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), vpKalmanFilter::prediction(), and setStateModel().
|
protectedinherited |
When set to true, print the content of internal variables during filtering() and prediction().
Definition at line 124 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::filtering(), and vpKalmanFilter::prediction().
|
protectedinherited |
Filter gain 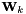 where
where ![$ {\bf W}_k = {\bf P}_{k \mid k-1} {\bf H}^T \left[ {\bf H P}_{k \mid k-1} {\bf H}^T + {\bf R}_k \right]^{-1}$](form_138.png) .
.
Definition at line 214 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::filtering().
|
inherited |
The updated state estimate 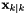 where
where ![${\bf x}_{k \mid k} = {\bf x}_{k \mid k-1} + {\bf W}_k \left[ {\bf z}_k - {\bf H x}_{k \mid k-1} \right]$](form_126.png) .
.
Definition at line 165 of file vpKalmanFilter.h.
Referenced by filter(), vpKalmanFilter::filtering(), vpKalmanFilter::init(), initStateConstAccWithColoredNoise_MeasureVel(), initStateConstVel_MeasurePos(), initStateConstVelWithColoredNoise_MeasureVel(), and vpKalmanFilter::prediction().
|
inherited |
The predicted state 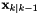 where
where 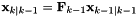 .
.
Definition at line 178 of file vpKalmanFilter.h.
Referenced by vpKalmanFilter::filtering(), vpKalmanFilter::init(), and vpKalmanFilter::prediction().