 |
ViSP
2.10.0
|
 |
ViSP
2.10.0
|
#include <vpRotationMatrix.h>
 Inheritance diagram for vpRotationMatrix:
Inheritance diagram for vpRotationMatrix:Public Types | |
| enum | vpDetMethod { LU_DECOMPOSITION } |
Public Member Functions | |
| void | init () |
| void | setIdentity () |
| void | eye () |
| vpRotationMatrix () | |
| vpRotationMatrix (const vpRotationMatrix &R) | |
| vpRotationMatrix (const vpHomogeneousMatrix &M) | |
| vpRotationMatrix (const vpThetaUVector &r) | |
| vpRotationMatrix (const vpPoseVector &p) | |
| vpRotationMatrix (const vpRzyzVector &r) | |
| vpRotationMatrix (const vpRxyzVector &r) | |
| vpRotationMatrix (const vpRzyxVector &r) | |
| vpRotationMatrix (const double tux, const double tuy, const double tuz) | |
| vpRotationMatrix (const vpQuaternionVector &q) | |
| vpRotationMatrix & | operator= (const vpRotationMatrix &R) |
| vpRotationMatrix & | operator= (const vpMatrix &m) |
| vpTranslationVector | operator* (const vpTranslationVector &mat) const |
| vpRotationMatrix | operator* (const vpRotationMatrix &B) const |
| vpMatrix | operator* (const vpMatrix &B) const |
| vpColVector | operator* (const vpColVector &v) const |
| vpRotationMatrix | operator+ (const vpRotationMatrix &B) const |
| vpRotationMatrix | operator- (const vpRotationMatrix &B) const |
| vpRotationMatrix | t () const |
| vpRotationMatrix | inverse () const |
| void | inverse (vpRotationMatrix &M) const |
| bool | isARotationMatrix () const |
| void | printVector () |
| vpRotationMatrix | buildFrom (const vpHomogeneousMatrix &M) |
| vpRotationMatrix | buildFrom (const vpThetaUVector &v) |
| vpRotationMatrix | buildFrom (const vpPoseVector &p) |
| vpRotationMatrix | buildFrom (const vpRzyzVector &v) |
| vpRotationMatrix | buildFrom (const vpRxyzVector &v) |
| vpRotationMatrix | buildFrom (const vpRzyxVector &v) |
| vpRotationMatrix | buildFrom (const double tux, const double tuy, const double tuz) |
| vpRotationMatrix | buildFrom (const vpQuaternionVector &q) |
| void | kill () |
| void | eye (unsigned int n) |
| void | eye (unsigned int m, unsigned int n) |
| void | setIdentity (const double &val=1.0) |
| void | insert (const vpMatrix &A, const unsigned int r, const unsigned int c) |
| void | stackMatrices (const vpMatrix &A) |
Columns, Rows extraction, Submatrix | |
| void | init (const vpMatrix &M, unsigned int r, unsigned int c, unsigned int nrows, unsigned int ncols) |
| vpRowVector | getRow (const unsigned int i) const |
| vpRowVector | getRow (const unsigned int i, const unsigned int j_begin, const unsigned int size) const |
| vpColVector | getCol (const unsigned int j) const |
| vpColVector | getCol (const unsigned int j, const unsigned int i_begin, const unsigned int size) const |
Set/get Matrix size | |
| unsigned int | getRows () const |
| unsigned int | getCols () const |
| unsigned int | size () const |
| void | resize (const unsigned int nrows, const unsigned int ncols, const bool nullify=true) |
| double | getMinValue () const |
| double | getMaxValue () const |
Copy / assignment | |
| vpMatrix & | operator<< (double *) |
| void | diag (const vpColVector &A) |
Printing | |
| int | print (std::ostream &s, unsigned int length, char const *intro=0) |
| std::ostream & | matlabPrint (std::ostream &os) const |
| std::ostream & | maplePrint (std::ostream &os) const |
| std::ostream & | csvPrint (std::ostream &os) const |
| std::ostream & | cppPrint (std::ostream &os, const char *matrixName=NULL, bool octet=false) const |
| void | printSize () |
Access/modification operators | |
| double * | operator[] (unsigned int i) |
| double * | operator[] (unsigned int i) const |
Kronecker product | |
| void | kron (const vpMatrix &m1, vpMatrix &out) |
| vpMatrix | kron (const vpMatrix &m1) |
| void | stackColumns (vpColVector &out) |
| vpColVector | stackColumns () |
| void | stackRows (vpRowVector &out) |
| vpRowVector | stackRows () |
Matrix operations | |
| vpMatrix & | operator+= (const vpMatrix &B) |
| vpMatrix & | operator+= (const double x) |
| vpMatrix & | operator-= (const vpMatrix &B) |
| vpMatrix & | operator-= (const double x) |
| vpMatrix | operator* (const vpHomography &H) const |
| vpMatrix | operator* (const double x) const |
| vpMatrix | operator+ (const vpMatrix &B) const |
| vpMatrix | operator- (const vpMatrix &B) const |
| vpMatrix | operator- () const |
| vpMatrix & | operator*= (const double x) |
| vpMatrix & | operator/= (double x) |
| vpMatrix | operator/ (const double x) const |
| double | sum () const |
| double | sumSquare () const |
| double | det (vpDetMethod method=LU_DECOMPOSITION) const |
| vpMatrix | expm () |
Transpose, Identity | |
| vpMatrix | transpose () const |
| void | transpose (vpMatrix &C) const |
| vpMatrix | AAt () const |
| void | AAt (vpMatrix &B) const |
| vpMatrix | AtA () const |
| void | AtA (vpMatrix &B) const |
Matrix inversion | |
| vpMatrix | inverseByLU () const |
| vpMatrix | inverseByCholesky () const |
| vpMatrix | inverseByCholeskyLapack () const |
| vpMatrix | inverseByQR () const |
| vpMatrix | inverseByQRLapack () const |
| vpMatrix | pseudoInverse (double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold=1e-6) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &ImA, vpMatrix &ImAt) const |
| unsigned int | pseudoInverse (vpMatrix &Ap, vpColVector &sv, double svThreshold, vpMatrix &ImA, vpMatrix &ImAt, vpMatrix &kerA) const |
SVD decomposition | |
| void | svd (vpColVector &w, vpMatrix &v) |
| void | solveBySVD (const vpColVector &B, vpColVector &x) const |
| vpColVector | solveBySVD (const vpColVector &B) const |
| unsigned int | kernel (vpMatrix &KerA, double svThreshold=1e-6) |
| double | cond () |
Eigen values | |
| vpColVector | eigenValues () |
| void | eigenValues (vpColVector &evalue, vpMatrix &evector) |
Norms | |
| double | euclideanNorm () const |
| double | infinityNorm () const |
Deprecated functions | |
| vp_deprecated vpRowVector | row (const unsigned int i) |
| vp_deprecated vpColVector | column (const unsigned int j) |
Static Public Member Functions | |
| static void | add2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | add2WeightedMatrices (const vpMatrix &A, const double &wA, const vpMatrix &B, const double &wB, vpMatrix &C) |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b) |
| static vpMatrix | computeCovarianceMatrix (const vpMatrix &A, const vpColVector &x, const vpColVector &b, const vpMatrix &w) |
| static void | computeHLM (const vpMatrix &H, const double &alpha, vpMatrix &HLM) |
| static void | createDiagonalMatrix (const vpColVector &A, vpMatrix &DA) |
| static vpMatrix | insert (const vpMatrix &A, const vpMatrix &B, const unsigned int r, const unsigned int c) |
| static void | insert (const vpMatrix &A, const vpMatrix &B, vpMatrix &C, const unsigned int r, const unsigned int c) |
| static vpMatrix | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B) |
| static void | juxtaposeMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | kron (const vpMatrix &m1, const vpMatrix &m2, vpMatrix &out) |
| static vpMatrix | kron (const vpMatrix &m1, const vpMatrix &m2) |
| static bool | loadMatrix (std::string filename, vpMatrix &M, const bool binary=false, char *Header=NULL) |
| static bool | loadMatrix (const char *filename, vpMatrix &M, const bool binary=false, char *Header=NULL) |
| static void | mult2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | multMatrixVector (const vpMatrix &A, const vpColVector &b, vpColVector &c) |
| static void | negateMatrix (const vpMatrix &A, vpMatrix &C) |
| static bool | saveMatrix (std::string filename, const vpMatrix &M, const bool binary=false, const char *Header="") |
| static bool | saveMatrix (const char *filename, const vpMatrix &M, const bool binary=false, const char *Header="") |
| static bool | saveMatrixYAML (std::string filename, const vpMatrix &M, const char *header="") |
| static bool | saveMatrixYAML (const char *filename, const vpMatrix &M, const char *header="") |
| static bool | loadMatrixYAML (std::string filename, vpMatrix &M, char *header=NULL) |
| static bool | loadMatrixYAML (const char *filename, vpMatrix &M, char *header=NULL) |
| static vpMatrix | stackMatrices (const vpMatrix &A, const vpMatrix &B) |
| static void | stackMatrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
| static void | sub2Matrices (const vpMatrix &A, const vpMatrix &B, vpMatrix &C) |
Public Attributes | |
| double * | data |
Protected Attributes | |
| unsigned int | rowNum |
| unsigned int | colNum |
| double ** | rowPtrs |
| unsigned int | dsize |
| unsigned int | trsize |
Friends | |
| class | vpMatrix |
| class | vpHomogeneousMatrix |
| class | vpRxyzVector |
| class | vpRzyzVector |
| class | vpRzyxVector |
| class | vpThetaUVector |
| class | vpTranslationVector |
| class | vpPoseVector |
| VISP_EXPORT std::ostream & | operator<< (std::ostream &s, const vpRotationMatrix &m) |
Related Functions | |
(Note that these are not member functions.) | |
| enum | vpGEMMmethod |
| vpMatrix | operator* (const double &x, const vpMatrix &B) |
| void | vpGEMM (const vpMatrix &A, const vpMatrix &B, const double &alpha, const vpMatrix &C, const double &beta, vpMatrix &D, const unsigned int &ops=0) |
| void | skew (const vpTranslationVector &t, vpMatrix &M) |
The vpRotationMatrix considers the particular case of a rotation matrix.
It is derived from vpMatrix.
Definition at line 74 of file vpRotationMatrix.h.
|
inherited |
Method used to compute the determinant of a square matrix.
| Enumerator | |
|---|---|
| LU_DECOMPOSITION |
LU decomposition method. |
Definition at line 105 of file vpMatrix.h.
| vpRotationMatrix::vpRotationMatrix | ( | ) |
Default constructor.
initialize a rotation matrix as Identity
Definition at line 353 of file vpRotationMatrix.cpp.
References init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpRotationMatrix & | R | ) |
Copy constructor.
initialize a rotation matrix from another rotation matrix
Definition at line 362 of file vpRotationMatrix.cpp.
References init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpHomogeneousMatrix & | M | ) |
Copy constructor.
Initialize a rotation matrix from an homogenous matrix.
Definition at line 370 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpThetaUVector & | r | ) |
Construction from rotation (theta U parameterization)
Construction from rotation (Theta U parameterization)
Definition at line 377 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpPoseVector & | p | ) |
Construction from a pose vector.
Definition at line 383 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpRzyzVector & | r | ) |
Construction from rotation (Euler parameterization)
Construction from rotation (Euler parameterization, ie Rzyz parameterization)
Definition at line 391 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpRxyzVector & | r | ) |
Construction from rotation Rxyz.
Definition at line 400 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpRzyxVector & | r | ) |
Construction from rotation Rzyx.
Definition at line 407 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
| vpRotationMatrix::vpRotationMatrix | ( | const double | tux, |
| const double | tuy, | ||
| const double | tuz | ||
| ) |
Construction from rotation (theta U parameterization)
Construction from rotation (Theta U parameterization)
Definition at line 414 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
| vpRotationMatrix::vpRotationMatrix | ( | const vpQuaternionVector & | q | ) |
Construct from rotation in quaternion representation.
Definition at line 423 of file vpRotationMatrix.cpp.
References buildFrom(), and init().
|
inherited |
Computes the 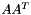 operation
operation 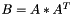
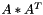
Definition at line 1368 of file vpMatrix.cpp.
|
inherited |
Compute the AAt operation such as 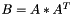 .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 1388 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
|
staticinherited |
Operation C = A + B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 602 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator+().
|
staticinherited |
Operation C = A*wA + B*wB
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 563 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Compute the AtA operation such as 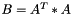
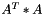
Definition at line 1479 of file vpMatrix.cpp.
Referenced by vpCalibration::calibrationTsai(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpTemplateTrackerWarpHomographySL3::findWarp(), and vpNurbs::globalCurveApprox().
|
inherited |
Compute the AtA operation such as 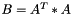 .
.
The result is placed in the parameter B and not returned.
A new matrix won't be allocated for every use of the function. This results in a speed gain if used many times with the same result matrix size.
Definition at line 1431 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrix::resize(), vpMatrix::rowNum, vpCERROR, and vpERROR_TRACE.
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const vpHomogeneousMatrix & | M | ) |
Build a rotation matrix from an homogeneous matrix.
Build a rotation matrix from an homogenous matrix.
Definition at line 593 of file vpRotationMatrix.cpp.
Referenced by vpVelocityTwistMatrix::buildFrom(), vpForceTwistMatrix::buildFrom(), buildFrom(), vpRzyzVector::buildFrom(), vpRzyxVector::buildFrom(), vpRxyzVector::buildFrom(), vpExponentialMap::direct(), vpRobotAfma6::setPosition(), and vpRotationMatrix().
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const vpThetaUVector & | v | ) |
Transform a vector vpThetaUVector into a rotation matrix.
Definition at line 510 of file vpRotationMatrix.cpp.
References vpMath::mcosc(), and vpMath::sinc().
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const vpPoseVector & | p | ) |
Transform a pose vector into a rotation matrix.
Definition at line 609 of file vpRotationMatrix.cpp.
References buildFrom().
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const vpRzyzVector & | v | ) |
Transform a vector reprensenting the euler (Rzyz) angle into a rotation matrix
Transform a vector representing the euler angle into a rotation matrix. Rzyz = Rot( 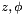 ) Rot(
) Rot( 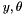 ) Rot(
) Rot( 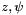 )
)
Definition at line 622 of file vpRotationMatrix.cpp.
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const vpRxyzVector & | v | ) |
Transform a vector reprensenting the Rxyz angle into a rotation matrix.
Transform a vector representing the Rxyz angle into a rotation matrix.
Rxyz( 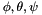 ) = Rot(
) = Rot( 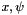 ) Rot(
) Rot( 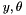 ) Rot(
) Rot( 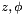 )
)
Definition at line 657 of file vpRotationMatrix.cpp.
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const vpRzyxVector & | v | ) |
Transform a vector reprensenting the Rzyx angle into a rotation matrix.
Transform a vector representing the Rzyx angle into a rotation matrix.
Rxyz( 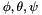 ) Rot(
) Rot( 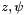 ) Rot(
) Rot( 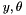 )Rot(
)Rot( 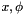 )
)
Definition at line 691 of file vpRotationMatrix.cpp.
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const double | tux, |
| const double | tuy, | ||
| const double | tuz | ||
| ) |
Construction from rotation (theta U parameterization)
Definition at line 721 of file vpRotationMatrix.cpp.
References buildFrom().
| vpRotationMatrix vpRotationMatrix::buildFrom | ( | const vpQuaternionVector & | q | ) |
Construction from rotation (as quaternion)
Definition at line 733 of file vpRotationMatrix.cpp.
References vpQuaternionVector::w(), vpQuaternionVector::x(), vpQuaternionVector::y(), and vpQuaternionVector::z().
|
inherited |
Return the j-th columns of the matrix.
| j | : Index of the column to extract. |
Definition at line 2362 of file vpMatrix.cpp.
References vpMatrix::getRows().
|
staticinherited |
Compute the covariance matrix of the parameters x from a least squares minimisation defined as: Ax = b
| A | : Matrix A from Ax = b. |
| x | : Vector x from Ax = b corresponding to the parameters to estimate. |
| b | : Vector b from Ax = b. |
Definition at line 61 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrix::pseudoInverse(), and vpMatrix::t().
Referenced by vpMbTracker::computeCovarianceMatrix(), vpPose::poseVirtualVS(), and vpPose::poseVirtualVSrobust().
|
staticinherited |
Compute the covariance matrix of the parameters x from a least squares minimisation defined as: WAx = Wb
| A | : Matrix A from WAx = Wb. |
| x | : Vector x from WAx = Wb corresponding to the parameters to estimate. |
| b | : Vector b from WAx = Wb. |
| W | : Diagonal weigths matrix from WAx = Wb. |
Definition at line 89 of file vpMatrix_covariance.cpp.
References vpException::divideByZeroError, vpMatrix::getCols(), and vpMatrix::t().
|
staticinherited |
Compute 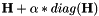
| H | : input Matrix 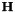 . This matrix should be square. . This matrix should be square. |
| alpha | : Scalar 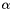 |
| HLM | : Resulting operation. |
Definition at line 4320 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), and vpTRACE.
Referenced by vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerSSDESM::initCompInverse(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), vpTemplateTrackerSSDESM::trackNoPyr(), and vpTemplateTrackerSSDForwardAdditional::trackNoPyr().
|
inherited |
Definition at line 4295 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::svd().
|
inherited |
Print to be used as part of a C++ code later.
Print under the following form: vpMatrix A(6,4); A[0][0] = 1.4; A[0][1] = 0.6; ...
| os | the stream to be printed in. |
| matrixName | name of the matrix, "A" by default, to be used for the line vpMatrix A(6,7) (see example). |
| octet | if false, print using double, if true, print byte per byte each bytes of the double array. |
Definition at line 3120 of file vpMatrix.cpp.
References vpMatrix::getRows().
|
staticinherited |
Create a diagonal matrix with the element of a vector 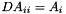 .
.
| A | : Vector which element will be put in the diagonal. |
| DA | : Diagonal matrix DA[i][i] = A[i] |
Definition at line 2869 of file vpMatrix.cpp.
References vpMatrix::getRows(), vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
|
inherited |
Print matrix in csv format.
Print as comma separated values so that this output can be imported into any program which has a csv data import option: 0.939846, 0.0300754, 0.340272 0.0300788, 0.984961, -0.170136 -0.340272, 0.170136, 0.924807
Definition at line 3087 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
|
inherited |
Compute the determinant of a n-by-n matrix.
| method | : Method used to compute the determinant. Default LU decomposition methos is faster than the method based on Gaussian elimination. |
Definition at line 3765 of file vpMatrix.cpp.
References vpMatrix::LU_DECOMPOSITION.
Referenced by vpTemplateTrackerTriangle::init().
|
inherited |
Create a diagonal matrix with the element of a vector.
| A | : Vector which element will be put in the diagonal. |
Definition at line 2841 of file vpMatrix.cpp.
References vpMatrix::getRows(), vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
Referenced by vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), and vpMbEdgeTracker::computeVVS().
|
inherited |
Compute the eigenvalues of a n-by-n real symmetric matrix.
| vpMatrixException::matrixError | If the matrix is not square or if the matrix is not symmetric. |
| vpMatrixException::notImplementedError | If the GSL library is not detected |
Here an example:
Definition at line 3348 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::matrixError, vpMatrixException::notImplementedError, vpMatrix::rowNum, vpMatrix::t(), and vpERROR_TRACE.
|
inherited |
Compute the eigenvalues of a n-by-n real symmetric matrix.
| evalue | : Eigenvalues of the matrix. |
| evector | : Eigenvector of the matrix. |
| vpMatrixException::matrixError | If the matrix is not square or if the matrix is not symmetric. |
| vpMatrixException::notImplementedError | If the GSL library is not detected |
Here an example:
Definition at line 3467 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrixException::matrixError, vpMatrixException::notImplementedError, vpColVector::resize(), vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::t(), and vpERROR_TRACE.
|
inherited |
Compute and return the Euclidean norm 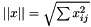 .
.
Definition at line 3168 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::dsize.
Referenced by vpSimulatorAfma6::setPosition().
|
inherited |
Compute the exponential matrix of a square matrix.
Definition at line 4137 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrixException::incorrectMatrixSizeError, vpMatrix::inverseByLU(), vpMatrix::rowNum, vpMatrix::setIdentity(), vpMatrix::sum(), and vpTRACE.
Referenced by vpTemplateTrackerWarpHomographySL3::computeCoeff().
| void vpRotationMatrix::eye | ( | ) |
Initialize the rotation matrix as identity.
Definition at line 110 of file vpRotationMatrix.cpp.
References init().
|
inherited |
Set an n-by-n matrix to identity.
eye(n) is an n-by-n matrix with ones on the diagonal and zeros else where.
Definition at line 1252 of file vpMatrix.cpp.
References vpCERROR, and vpERROR_TRACE.
Referenced by vpMbEdgeTracker::computeVVS(), and vpServo::setServo().
|
inherited |
Set an m-by-n matrix to identity.
eye(m,n) is an m-by-n matrix with ones on the diagonal and zeros else where.
Definition at line 1272 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpCERROR, and vpERROR_TRACE.
|
inherited |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If j=0, the first column is extracted. |
The following example shows how to use this function:
It produces the following output:
Definition at line 2463 of file vpMatrix.cpp.
References vpException::dimensionError, vpMatrix::getCols(), and vpMatrix::getRows().
Referenced by vpHomography::DLT(), vpPose::poseDementhonPlan(), and vpPose::poseFromRectangle().
|
inherited |
Extract a column vector from a matrix.
| j | : Index of the column to extract. If col=0, the first column is extracted. |
| i_begin | : Index of the row that gives the location of the first element of the column vector to extract. |
| column_size | : Size of the column vector to extract. |
The following example shows how to use this function:
It produces the following output:
Definition at line 2413 of file vpMatrix.cpp.
References vpException::dimensionError, vpMatrix::getCols(), and vpMatrix::getRows().
|
inlineinherited |
Return the number of columns of the matrix.
Definition at line 163 of file vpMatrix.h.
Referenced by vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpSubRowVector::checkParentStatus(), vpSubMatrix::checkParentStatus(), vpServo::computeControlLaw(), vpMatrix::computeCovarianceMatrix(), vpMatrix::computeHLM(), vpServo::computeInteractionMatrix(), vpMbTracker::computeJTR(), vpMatrix::cond(), vpMatrix::csvPrint(), vpMatrix::getCol(), vpImageSimulator::getImage(), vpMatrix::getRow(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpCameraParameters::initFromCalibrationMatrix(), vpMatrix::insert(), vpMatrix::inverseByCholeskyLapack(), vpMatrix::inverseByQRLapack(), vpMatrix::juxtaposeMatrices(), vpMatrix::kernel(), vpMatrix::kron(), vpMatrix::maplePrint(), vpRowVector::operator*(), operator*(), vpVelocityTwistMatrix::operator*(), vpForceTwistMatrix::operator*(), vpMatrix::operator*(), vpRowVector::operator+(), vpMatrix::operator+=(), vpRowVector::operator-(), vpMatrix::operator-=(), vpSubRowVector::operator=(), vpSubColVector::operator=(), vpSubMatrix::operator=(), vpRowVector::operator=(), vpColVector::operator=(), operator=(), vpHomography::operator=(), vpPose::poseDementhonPlan(), vpMatrix::print(), vpMatrix::pseudoInverse(), vpIoTools::readConfigVar(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::row(), vpMatrix::saveMatrix(), vpMatrix::saveMatrixYAML(), vpServo::secondaryTask(), vpRowVector::size(), vpMatrix::stackMatrices(), vpMatrix::sub2Matrices(), and vpMatrix::svd().
|
inherited |
Definition at line 4238 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::dsize.
|
inherited |
Definition at line 4224 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::dsize.
|
inherited |
Extract a row vector from a matrix.
| i | : Index of the row to extract. If i=0, the first row is extracted. |
The following example shows how to use this function:
It produces the following output:
Definition at line 2510 of file vpMatrix.cpp.
References vpException::dimensionError, vpMatrix::getCols(), and vpMatrix::getRows().
Referenced by vpMatrix::kernel(), and vpMatrix::pseudoInverse().
|
inherited |
Extract a row vector from a matrix.
| i | : Index of the row to extract. If i=0, the first row is extracted. |
| j_begin | : Index of the column that gives the location of the first element of the row vector to extract. |
| row_size | : Size of the row vector to extract. |
The following example shows how to use this function:
It produces the following output:
Definition at line 2559 of file vpMatrix.cpp.
References vpException::dimensionError, vpMatrix::getCols(), and vpMatrix::getRows().
|
inlineinherited |
Return the number of rows of the matrix.
Definition at line 161 of file vpMatrix.h.
Referenced by vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpLine::changeFrame(), vpSubColVector::checkParentStatus(), vpSubMatrix::checkParentStatus(), vpMatrix::column(), vpServo::computeControlLaw(), vpMatrix::computeCovarianceMatrix(), vpMbTracker::computeCovarianceMatrix(), vpServo::computeError(), vpMatrix::computeHLM(), vpServo::computeInteractionMatrix(), vpMbTracker::computeJTR(), vpPtu46::computeMGD(), vpPose::computeResidual(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpMatrix::cppPrint(), vpMatrix::createDiagonalMatrix(), vpColVector::crossProd(), vpMatrix::csvPrint(), vpDot2::defineDots(), vpMatrix::diag(), vpProjectionDisplay::display(), vpColVector::dotProd(), vpGenericFeature::error(), vpImageFilter::filter(), vpPtu46::get_eJe(), vpBiclops::get_eJe(), vpPtu46::get_fJe(), vpBiclops::get_fJe(), vpBiclops::get_fMe(), vpGenericFeature::get_s(), vpMatrix::getCol(), vpBasicFeature::getDimension(), vpImageSimulator::getImage(), vpAfma6::getInverseKinematics(), vpViper::getInverseKinematicsWrist(), vpMatrix::getRow(), vpSubColVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpCameraParameters::initFromCalibrationMatrix(), vpMatrix::insert(), vpFeatureLuminance::interaction(), vpGenericFeature::interaction(), vpMatrix::inverseByCholeskyLapack(), vpMatrix::inverseByLU(), vpMatrix::inverseByQRLapack(), vpColVector::invSort(), vpMatrix::juxtaposeMatrices(), vpMatrix::kernel(), vpScale::KernelDensity(), vpScale::KernelDensityGradient(), vpMatrix::kron(), vpMatrix::maplePrint(), vpMatrix::matlabPrint(), vpColVector::mean(), vpScale::MeanShift(), vpColVector::median(), vpRobust::MEstimator(), vpMatrix::multMatrixVector(), vpRowVector::operator*(), operator*(), vpVelocityTwistMatrix::operator*(), vpForceTwistMatrix::operator*(), vpMatrix::operator*(), vpColVector::operator+(), vpMatrix::operator+=(), vpColVector::operator-(), vpMatrix::operator-=(), vpSubColVector::operator=(), vpSubRowVector::operator=(), vpSubMatrix::operator=(), vpColVector::operator=(), operator=(), vpRGBa::operator=(), vpHomography::operator=(), vpPlot::plot(), vpPose::poseDementhonPlan(), vpPose::poseVirtualVSrobust(), vpKalmanFilter::prediction(), vpMatrix::print(), vpLine::projection(), vpMatrix::pseudoInverse(), vpIoTools::readConfigVar(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::saveMatrix(), vpMatrix::saveMatrixYAML(), vpGenericFeature::set_s(), vpGenericFeature::setError(), vpMbTracker::setEstimatedDoF(), vpGenericFeature::setInteractionMatrix(), vpSimulatorAfma6::setJointLimit(), vpSimulatorViper850::setJointLimit(), vpRobotBiclopsController::setPosition(), vpRobotAfma4::setPosition(), vpRobotBiclopsController::setVelocity(), vpRobotPtu46::setVelocity(), vpRobotBiclops::setVelocity(), vpSimulatorAfma6::setVelocity(), vpSimulatorViper850::setVelocity(), vpRobotAfma4::setVelocity(), vpLine::setWorldCoordinates(), vpRobust::simultMEstimator(), vpColVector::size(), vpColVector::skew(), vpColVector::sort(), vpColVector::stack(), vpMatrix::stackMatrices(), vpMatrix::sub2Matrices(), vpMatrix::svd(), and vpColVector::vpColVector().
|
inherited |
Compute and return the infinity norm 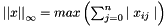 with
with 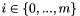 where
where 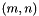 is the matrix size.
is the matrix size.
Definition at line 3192 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
| void vpRotationMatrix::init | ( | ) |
Basic initialisation (identity)
Initializes a 3x3 rotation matrix as identity
Definition at line 73 of file vpRotationMatrix.cpp.
References vpMatrix::resize(), and vpERROR_TRACE.
Referenced by eye(), setIdentity(), and vpRotationMatrix().
|
inherited |
Initialize the matrix from a part of an input matrix M.
| M | : Input matrix used for initialization. |
| r | : row index in matrix M. |
| c | : column index in matrix M. |
| nrows | : Number of rows of the matrix that should be initialized. |
| ncols | : Number of columns of the matrix that should be initialized. |
The sub-matrix starting from M[r][c] element and ending on M[r+nrows-1][c+ncols-1] element is used to initialize the matrix.
The following code shows how to use this function:
It produces the following output:
Definition at line 331 of file vpMatrix.cpp.
References vpException::dimensionError, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrix::resize(), and vpMatrix::rowPtrs.
|
inherited |
Insert matrix A at the given position in the current matrix.
| A | : The matrix to insert. |
| r | : The index of the row to begin to insert data. |
| c | : The index of the column to begin to insert data. |
Definition at line 3291 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, and vpMatrix::rowNum.
Referenced by vpNurbs::curveKnotIns(), vpMatrix::insert(), vpPioneerPan::set_mMp(), and vpPioneerPan::set_pMe().
|
staticinherited |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| r | : Index of the row where to add the matrix. |
| c | : Index of the column where to add the matrix. |
Definition at line 2666 of file vpMatrix.cpp.
References vpMatrix::insert(), and vpCERROR.
|
staticinherited |
Insert matrix B in matrix A at the given position.
| A | : Main matrix. |
| B | : Matrix to insert. |
| C | : Result matrix. |
| r | : Index of the row where to insert matrix B. |
| c | : Index of the column where to insert matrix B. |
Definition at line 2697 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
| vpRotationMatrix vpRotationMatrix::inverse | ( | ) | const |
invert the rotation matrix
inverse the rotation matrix
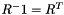
Definition at line 452 of file vpRotationMatrix.cpp.
References t().
Referenced by vpViper::get_eJe(), and inverse().
| void vpRotationMatrix::inverse | ( | vpRotationMatrix & | M | ) | const |
invert the rotation matrix
inverse the rotation matrix
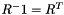
Definition at line 465 of file vpRotationMatrix.cpp.
References inverse().
|
inherited |
Compute the inverse of a n-by-n matrix using the Cholesky decomposition. The matrix must be real and symmetric. Only available if lapack is installed.
Here an example:
Definition at line 122 of file vpMatrix_cholesky.cpp.
References vpMatrix::colNum, vpMatrix::inverseByCholeskyLapack(), vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
|
inherited |
Definition at line 62 of file vpMatrix_cholesky.cpp.
References vpException::badValue, vpMatrix::data, vpMatrix::getCols(), and vpMatrix::getRows().
Referenced by vpMatrix::inverseByCholesky().
|
inherited |
Compute the inverse of a n-by-n matrix using the LU decomposition.
Here an example:
Definition at line 236 of file vpMatrix_lu.cpp.
References vpMatrix::colNum, vpMatrix::getRows(), vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
Referenced by vpMatrix::expm(), vpKalmanFilter::filtering(), vpTemplateTrackerWarpHomographySL3::findWarp(), vpTemplateTrackerWarpAffine::getParamInverse(), vpTemplateTrackerTriangle::init(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpTemplateTrackerZNCCForwardAdditional::initHessienDesired(), vpTemplateTrackerZNCCInverseCompositional::initHessienDesired(), vpTemplateTracker::setHDes(), vpTemplateTrackerSSDForwardCompositional::trackNoPyr(), and vpTemplateTrackerSSDForwardAdditional::trackNoPyr().
|
inherited |
Compute the inverse of a n-by-n matrix using the QR decomposition. Only available if lapack is installed.
Here an example:
Definition at line 228 of file vpMatrix_qr.cpp.
References vpMatrix::colNum, vpMatrix::inverseByQRLapack(), vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
|
inherited |
Definition at line 76 of file vpMatrix_qr.cpp.
References vpException::badValue, vpMatrix::data, vpMatrix::getCols(), and vpMatrix::getRows().
Referenced by vpMatrix::inverseByQR().
| bool vpRotationMatrix::isARotationMatrix | ( | ) | const |
test if the matrix is an rotation matrix
test if the 3x3 rotational part of the rotation matrix is really a rotation matrix
Definition at line 314 of file vpRotationMatrix.cpp.
References vpMath::sqr(), and t().
Referenced by vpHomogeneousMatrix::isAnHomogeneousMatrix(), and operator=().
Juxtapose to matrices C = [ A B ].
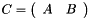
| A | : Left matrix. |
| B | : Right matrix. |
Definition at line 2740 of file vpMatrix.cpp.
References vpCERROR.
Juxtapose to matrices C = [ A B ].
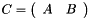
| A | : Left matrix. |
| B | : Right matrix. |
| C | : Juxtaposed matrix C = [ A B ] |
Definition at line 2769 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
|
inherited |
Function to compute the null space (the kernel) of the interaction matrix A which is not full rank. The null space ( the kernel ) of a matrix A is defined as Null(A) = Ker(M) ={KerA : A*KerA =0}.
| kerA | : The matrix to contain the null space (kernel) of A (A*KerA.t()=0) |
| svThreshold | : Specify the used threshold in the svd(...) function (a function to compute the singular value decomposition) |
Definition at line 3569 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRow(), vpMatrix::getRows(), vpMatrix::resize(), vpMatrix::sumSquare(), and vpMatrix::svd().
|
inherited |
Destruction of the matrix (Memory de-allocation)
Definition at line 355 of file vpMatrix.cpp.
References vpMatrix::data, and vpMatrix::rowPtrs.
Referenced by vpMatrix::~vpMatrix().
Compute Kronecker product matrix.
Definition at line 1563 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::rowNum, and vpERROR_TRACE.
Referenced by vpMatrix::kron().
Compute Kronecker product matrix.

Definition at line 1607 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
Compute Kronecker product matrix.
| m | : vpMatrix. |
| out | : If m1.kron(m2) out contains the kronecker product's result :  . . |
Definition at line 1597 of file vpMatrix.cpp.
References vpMatrix::kron().
Compute Kronecker product matrix.
| m | : vpMatrix; |

Definition at line 1638 of file vpMatrix.cpp.
References vpMatrix::kron().
|
inlinestaticinherited |
Load a matrix from a file.
| filename | : absolute file name |
| M | : matrix to be loaded |
| binary | :If true the matrix is loaded from a binary file, else from a text file. |
| Header | : Header of the file is loaded in this parameter |
Definition at line 264 of file vpMatrix.h.
Referenced by vpDot2::defineDots().
|
staticinherited |
Load a matrix from a file.
| filename | : Absolute file name. |
| M | : Matrix to be loaded. |
| binary | : If true the matrix is loaded from a binary file, else from a text file. |
| header | : header of the file loaded in this parameter. |
Definition at line 3963 of file vpMatrix.cpp.
References vpException::badValue, and vpMatrix::resize().
|
inlinestaticinherited |
Load a matrix from a YAML-formatted file.
| filename | : absolute file name. |
| M | : matrix to be loaded from the file. |
| header | : Header of the file is loaded in this parameter. |
Definition at line 317 of file vpMatrix.h.
|
staticinherited |
Load a matrix from a YAML-formatted file.
| filename | : absolute file name. |
| M | : matrix to be loaded from the file. |
| header | : header of the file is loaded in this parameter. |
Definition at line 4060 of file vpMatrix.cpp.
References vpMatrix::resize().
|
inherited |
Print using MAPLE matrix input format.
Print using the following way so that this output can be directly copied into MAPLE: ([ [0.939846, 0.0300754, 0.340272, ], [0.0300788, 0.984961, -0.170136, ], [-0.340272, 0.170136, 0.924807, ], ])
Definition at line 3061 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
|
inherited |
Print using matlab syntax, to be put in matlab later.
Print using the following form: [ a,b,c; d,e,f; g,h,i]
Definition at line 3032 of file vpMatrix.cpp.
References vpMatrix::getRows().
|
staticinherited |
Operation C = A * B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 480 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator*().
|
staticinherited |
Operation c = A * b (c and b are vectors).
The result is placed in the second parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 931 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpColVector::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by operator*(), and vpMatrix::operator*().
Operation C = -A.
The result is placed in the second parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 818 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator-().
| vpTranslationVector vpRotationMatrix::operator* | ( | const vpTranslationVector & | mat | ) | const |
operation c = A * b (A is unchanged)
Definition at line 292 of file vpRotationMatrix.cpp.
References vpMatrix::rowPtrs.
| vpRotationMatrix vpRotationMatrix::operator* | ( | const vpRotationMatrix & | B | ) | const |
operation C = A * B (A is unchanged)
Definition at line 170 of file vpRotationMatrix.cpp.
References vpMatrix::rowPtrs.
operation C = A * B (A is unchanged)
Operation C = A * B (A is unchanged). Allows for example to multiply a rotation matrix by a skew matrix.
| vpMatrixException::incorrectMatrixSizeError | : If B is not a 3 by 3 dimension matrix. |
Definition at line 199 of file vpRotationMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, and vpERROR_TRACE.
| vpColVector vpRotationMatrix::operator* | ( | const vpColVector & | v | ) | const |
Operator that allows to multiply a rotation matrix by a 3 dimension column vector.
| v | : Three dimension column vector. |
| vpMatrixException::incorrectMatrixSizeError | If the column vector v is not a 3 dimension vector. |
The code below shows how to use this operator.
Definition at line 249 of file vpRotationMatrix.cpp.
References vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::multMatrixVector(), and vpERROR_TRACE.
|
inherited |
Allows to multiply a matrix by an homography. Operation M = K * H (H is unchanged).
Definition at line 536 of file vpMatrix.cpp.
References vpMatrix::colNum, vpException::dimensionError, and vpMatrix::rowNum.
|
inherited |
Cij = Aij * x (A is unchanged)
Definition at line 1050 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Multiply all the element of the matrix by x : Aij = Aij * x.
Definition at line 1178 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
| vpRotationMatrix vpRotationMatrix::operator+ | ( | const vpRotationMatrix & | B | ) | const |
overload + operator (to say it forbidden operation, throw exception)
overload + operator (to say it forbidden operation, throw exception)
| Cannot | add two rotation matrices !!!!! vpMatrixException::forbiddenOperatorError |
Definition at line 269 of file vpRotationMatrix.cpp.
References vpMatrixException::forbiddenOperatorError, and vpERROR_TRACE.
Operation C = A + B (A is unchanged).
Definition at line 653 of file vpMatrix.cpp.
References vpMatrix::add2Matrices().
Operation A = A + B.
Definition at line 733 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Add x to all the element of the matrix : Aij = Aij + x.
Definition at line 1130 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
| vpRotationMatrix vpRotationMatrix::operator- | ( | const vpRotationMatrix & | B | ) | const |
overload - operator (to say it forbidden operation, throw exception)
overload - operator (to say it forbidden operation, throw exception)
| Cannot | substract two rotation matrices !!!!! vpMatrixException::forbiddenOperatorError |
Definition at line 283 of file vpRotationMatrix.cpp.
References vpMatrixException::forbiddenOperatorError, and vpERROR_TRACE.
Operation C = A - B (A is unchanged).
Definition at line 724 of file vpMatrix.cpp.
References vpMatrix::sub2Matrices().
|
inherited |
Operation C = -A (A is unchanged).
Definition at line 860 of file vpMatrix.cpp.
References vpMatrix::negateMatrix().
Operation A = A - B.
Definition at line 773 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
|
inherited |
Substract x to all the element of the matrix : Aij = Aij - x.
Definition at line 1154 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
|
inherited |
Cij = Aij / x (A is unchanged)
Definition at line 1085 of file vpMatrix.cpp.
References vpMatrix::colNum, vpException::divideByZeroError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
|
inherited |
Divide all the element of the matrix by x : Aij = Aij / x.
Definition at line 1193 of file vpMatrix.cpp.
References vpMatrix::colNum, vpException::divideByZeroError, vpMatrix::rowNum, and vpMatrix::rowPtrs.
|
inherited |
Assigment from an array of double.
Definition at line 455 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
| vpRotationMatrix & vpRotationMatrix::operator= | ( | const vpRotationMatrix & | m | ) |
copy operator from vpRotationMatrix
Return the 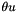 vector that corresponds to tha rotation matrix.
vector that corresponds to tha rotation matrix.
Affectation of two rotation matrix.
| m | : *this = m |
Definition at line 121 of file vpRotationMatrix.cpp.
References vpMatrix::rowPtrs.
| vpRotationMatrix & vpRotationMatrix::operator= | ( | const vpMatrix & | m | ) |
copy operator from vpMatrix (handle with care)
Affectation of two rotation matrix
| m | : *this = m |
Definition at line 140 of file vpRotationMatrix.cpp.
References vpMatrixException::forbiddenOperatorError, vpMatrix::getCols(), vpMatrix::getRows(), isARotationMatrix(), and vpERROR_TRACE.
|
inlineinherited |
write elements Aij (usage : A[i][j] = x )
Definition at line 220 of file vpMatrix.h.
|
inlineinherited |
read elements Aij (usage : x = A[i][j] )
Definition at line 222 of file vpMatrix.h.
|
inherited |
Pretty print a matrix. The data are tabulated. The common widths before and after the decimal point are set with respect to the parameter maxlen.
| s | Stream used for the printing. |
| length | The suggested width of each matrix element. The actual width grows in order to accomodate the whole integral part, and shrinks if the whole extent is not needed for all the numbers. |
| intro | The introduction which is printed before the matrix. Can be set to zero (or omitted), in which case the introduction is not printed. |
Definition at line 2937 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), and vpMath::maximum().
|
inlineinherited |
Definition at line 190 of file vpMatrix.h.
| void vpRotationMatrix::printVector | ( | ) |
Print the matrix as a vector [T thetaU].
Print the matrix as a vector [thetaU].
Definition at line 486 of file vpRotationMatrix.cpp.
|
inherited |
Compute the pseudo inverse of the matrix using the SVD.
Compute and return the pseudo inverse of a n-by-m matrix : 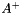 .
.
| svThreshold | : Threshold used to test the singular values. |
Here an example to compute the inverse of a n-by-n matrix. If the matrix is n-by-n it is also possible to use inverseByLU().
Definition at line 1932 of file vpMatrix.cpp.
Referenced by vpCalibration::calibrationTsai(), vpSimulatorAfma6::computeArticularVelocity(), vpSimulatorViper850::computeArticularVelocity(), vpServo::computeControlLaw(), vpMatrix::computeCovarianceMatrix(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpNurbs::globalCurveApprox(), vpNurbs::globalCurveInterp(), vpMeEllipse::initTracking(), vpHomography::inverse(), vpMeLine::leastSquare(), vpPose::poseDementhonNonPlan(), vpPose::poseFromRectangle(), vpPose::poseVirtualVS(), vpMatrix::pseudoInverse(), vpHomography::robust(), and vpMatrix::solveBySVD().
|
inherited |
Compute the pseudo inverse of the matrix 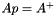 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank
| Ap | : The pseudo inverse 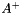 . . |
| svThreshold | : Threshold used to test the singular values. |
Definition at line 1892 of file vpMatrix.cpp.
References vpMatrix::pseudoInverse().
|
inherited |
Compute the pseudo inverse of the matrix 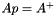 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank and the singular value
| Ap | : The pseudo inverse 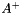 . . |
| sv | : Singular values. |
| svThreshold | : Threshold used to test the singular values. |
Definition at line 1948 of file vpMatrix.cpp.
References vpMatrix::pseudoInverse().
|
inherited |
Compute the pseudo inverse of the matrix 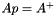 along with Ker A, Ker
along with Ker A, Ker 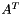 , Im A and Im
, Im A and Im 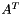 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank and the singular value, image
Pseudo inverse, kernel and image are computed using the SVD decomposition.
A is an m x n matrix, if m >=n the svd works on A other wise it works on 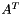 .
.
Therefore if m>=n we have
![\[ {\bf A}_{m\times n} = {\bf U}_{m\times m} {\bf S}_{m\times n} {\bf V^\top}_{n\times n} \]](form_223.png)
![\[ {\bf A}_{m\times n} = \left[\begin{array}{ccc}\mbox{Im} {\bf A} & | & \mbox{Ker} {\bf A^\top} \end{array} \right] {\bf S} \left[ \begin{array}{c} (\mbox{Im} {\bf A^\top})^\top \\ (\mbox{Ker}{\bf A})^\top \end{array}\right] \]](form_224.png)
where Im(A) is an m x r matrix (r is the rank of A) and Im(A^T) is an r x n matrix
| Ap | : The pseudo inverse 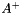 . . |
| sv | : Singular values. |
| svThreshold | : Threshold used to test the singular values. |
| imAt | : Image A^T |
| imA | Image A |
Definition at line 1987 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpColVector::resize(), vpMatrix::resize(), vpMatrix::svd(), and vpMatrix::t().
|
inherited |
Compute the pseudo inverse of the matrix 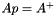 along with Ker A, Ker
along with Ker A, Ker 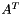 , Im A and Im
, Im A and Im 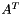 .
.
Compute the pseudo inverse of the matrix using the SVD. return the rank and the singular value, image, kernel.
Pseudo inverse, kernel and image are computed using the SVD decomposition.
A is an m x n matrix, if m >=n the svd works on A other wise it works on 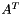 .
.
Therefore if m>=n we have
![\[ {\bf A}_{m\times n} = {\bf U}_{m\times m} {\bf S}_{m\times n} {\bf V^\top}_{n\times n} \]](form_223.png)
![\[ {\bf A}_{m\times n} = \left[\begin{array}{ccc}\mbox{Im} {\bf A} & | & \mbox{Ker} {\bf A^\top} \end{array} \right] {\bf S} \left[ \begin{array}{c} (\mbox{Im} {\bf A^\top})^\top \\ (\mbox{Ker}{\bf A})^\top \end{array}\right] \]](form_224.png)
where Im(A) is an m x r matrix (r is the rank of A) and Im(A^T) is an r x n matrix
| Ap | : The pseudo inverse 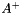 . . |
| sv | : Singular values. |
| svThreshold | : Threshold used to test the singular values. |
| imA | Image A |
| imAt | : Image A^T |
| kerA | : null space of A |
Definition at line 2165 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRow(), vpMatrix::getRows(), vpColVector::resize(), vpMatrix::resize(), vpMatrix::sumSquare(), vpMatrix::svd(), and vpMatrix::t().
|
inherited |
Set the size of the matrix and initialize all the values to zero.
| nrows | : number of rows |
| ncols | : number of column |
| flagNullify | : if true, then the matrix is re-initialized to 0 after resize. If false, the initial values from the common part of the matrix (common part between old and new version of the matrix) are kept. Default value is true. |
Definition at line 199 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrix::dsize, vpException::memoryAllocationError, vpMatrix::rowNum, vpMatrix::rowPtrs, vpMatrix::trsize, vpCDEBUG, vpDEBUG_TRACE, and vpERROR_TRACE.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::AtA(), vpServo::computeControlLaw(), vpMatrix::computeHLM(), vpMbTracker::computeJTR(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMatrix::createDiagonalMatrix(), vpMatrix::diag(), vpProjectionDisplay::display(), vpHomography::DLT(), vpMatrix::eigenValues(), vpMatrix::eye(), vpPtu46::get_eJe(), vpAfma4::get_eJe(), vpAfma6::get_eJe(), vpBiclops::get_eJe(), vpPtu46::get_fJe(), vpAfma4::get_fJe(), vpAfma6::get_fJe(), vpBiclops::get_fJe(), vpAfma4::get_fJe_inverse(), vpViper::get_fJw(), vpCameraParameters::get_K(), vpCameraParameters::get_K_inverse(), init(), vpProjectionDisplay::init(), vpVelocityTwistMatrix::init(), vpForceTwistMatrix::init(), vpKalmanFilter::init(), vpHomogeneousMatrix::init(), vpMatrix::init(), vpTemplateTrackerSSDInverseCompositional::initCompInverse(), vpMbtDistanceCircle::initInteractionMatrixError(), vpMbtDistanceCylinder::initInteractionMatrixError(), vpTemplateTracker::initTracking(), vpMatrix::insert(), vpFeatureEllipse::interaction(), vpFeatureVanishingPoint::interaction(), vpFeatureLuminance::interaction(), vpFeatureSegment::interaction(), vpGenericFeature::interaction(), vpFeatureDepth::interaction(), vpFeaturePoint::interaction(), vpFeatureLine::interaction(), vpFeaturePoint3D::interaction(), vpFeaturePointPolar::interaction(), vpFeatureThetaU::interaction(), vpFeatureTranslation::interaction(), vpMatrix::juxtaposeMatrices(), vpMatrix::kernel(), vpMatrix::loadMatrix(), vpMatrix::loadMatrixYAML(), vpMatrix::mult2Matrices(), vpMatrix::negateMatrix(), vpMatrix::operator*(), vpMatrix::operator/(), vpMatrix::operator=(), vpPose::poseDementhonPlan(), vpPose::poseVirtualVSrobust(), vpMatrix::pseudoInverse(), vpIoTools::readConfigVar(), vpRowVector::reshape(), vpColVector::reshape(), vpRowVector::resize(), vpColVector::resize(), vpServo::secondaryTask(), vpTemplateTrackerWarp::setNbParam(), vpColVector::skew(), vpMatrix::skew(), vpMatrix::stackMatrices(), vpMatrix::sub2Matrices(), vpMatrix::svd(), vpMatrix::t(), vpMatrix::transpose(), vpMatrix::vpMatrix(), vpTemplateTrackerSSD::vpTemplateTrackerSSD(), vpTemplateTrackerSSDESM::vpTemplateTrackerSSDESM(), vpTemplateTrackerSSDInverseCompositional::vpTemplateTrackerSSDInverseCompositional(), vpTemplateTrackerWarpAffine::vpTemplateTrackerWarpAffine(), vpTemplateTrackerWarpHomography::vpTemplateTrackerWarpHomography(), vpTemplateTrackerWarpHomographySL3::vpTemplateTrackerWarpHomographySL3(), vpTemplateTrackerWarpSRT::vpTemplateTrackerWarpSRT(), vpTemplateTrackerWarpTranslation::vpTemplateTrackerWarpTranslation(), and vpTemplateTrackerZNCC::vpTemplateTrackerZNCC().
|
inherited |
Return the i-th row of the matrix.
Definition at line 2346 of file vpMatrix.cpp.
References vpMatrix::getCols().
|
inlinestaticinherited |
Save a matrix to a file.
| filename | : absolute file name |
| M | : matrix to be saved |
| binary | :If true the matrix is save in a binary file, else a text file. |
| Header | : optional line that will be saved at the beginning of the file |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 285 of file vpMatrix.h.
Referenced by vpDot2::defineDots().
|
staticinherited |
Save a matrix to a file.
| filename | : Absolute file name. |
| M | : Matrix to be saved. |
| binary | : If true the matrix is saved in a binary file, else a text file. |
| header | : Optional line that will be saved at the beginning of the file. |
Warning : If you save the matrix as in a text file the precision is less than if you save it in a binary file.
Definition at line 3792 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
|
inlinestaticinherited |
Save a matrix in a YAML-formatted file.
| filename | : absolute file name. |
| M | : matrix to be saved in the file. |
| header | : optional lines that will be saved at the beginning of the file. Should be YAML-formatted and will adapt to the indentation if any. |
Definition at line 303 of file vpMatrix.h.
|
staticinherited |
Save a matrix in a YAML-formatted file.
| filename | : absolute file name. |
| M | : matrix to be saved in the file. |
| header | : optional lines that will be saved at the beginning of the file. Should be YAML-formatted and will adapt to the indentation if any. |
Here is an example of outputs.
Content of matrix.yml:
Content of matrixIndent.yml:
Definition at line 3892 of file vpMatrix.cpp.
References vpMatrix::getCols(), and vpMatrix::getRows().
| void vpRotationMatrix::setIdentity | ( | ) |
Basic initialisation (identity)
Initializes the rotation matrix as identity.
Definition at line 100 of file vpRotationMatrix.cpp.
References init().
Referenced by vpCalibration::calibrationTsai(), and vpHomography::computeDisplacement().
|
inherited |
By default set the matrix to identity. More generally set M[i][i] = val.
Definition at line 1230 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrixException::matrixError, vpMatrix::rowNum, and vpERROR_TRACE.
Referenced by vpServo::computeControlLaw(), vpMbTracker::computeCovarianceMatrix(), vpMatrix::expm(), vpTemplateTrackerWarpHomographySL3::getdW0(), vpTemplateTrackerWarpHomographySL3::getdWdp0(), vpFeatureThetaU::interaction(), vpMeLine::leastSquare(), vpPose::poseFromRectangle(), vpServo::secondaryTask(), and vpMbTracker::vpMbTracker().
|
inlineinherited |
Return the number of elements of the matrix.
Definition at line 165 of file vpMatrix.h.
|
inherited |
Solve a linear system 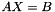 using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| b | : Vector 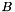 . . |
| x | : Vector 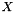 . . |
Here an example:
Definition at line 1693 of file vpMatrix.cpp.
References vpMatrix::pseudoInverse().
Referenced by vpMatrix::solveBySVD().
|
inherited |
Solve a linear system 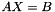 using Singular Value Decomposition (SVD).
using Singular Value Decomposition (SVD).
Non destructive wrt. A and B.
| B | : Vector 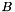 . . |
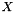 .
.Here an example:
Definition at line 1748 of file vpMatrix.cpp.
References vpMatrix::colNum, and vpMatrix::solveBySVD().
|
inherited |
Stacks columns of a matrix in a vector.
| out | : a vpColVector. |
Definition at line 1493 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpColVector::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
|
inherited |
Stacks columns of a matrix in a vector.
Definition at line 1517 of file vpMatrix.cpp.
References vpMatrix::colNum, and vpMatrix::rowNum.
|
inherited |
Stack A at the end of the current matrix, or copy if the matrix has no dimensions : this = [ this A ]^T
Here an example for a robot velocity log :
Definition at line 3272 of file vpMatrix.cpp.
References vpMatrix::rowNum.
Referenced by vpCalibration::calibrationTsai(), vpMbEdgeKltTracker::computeVVS(), vpFeatureSegment::error(), vpFeatureEllipse::error(), vpFeatureVanishingPoint::error(), vpFeatureMomentAlpha::error(), vpGenericFeature::error(), vpFeaturePoint::error(), vpFeatureLine::error(), vpFeaturePoint3D::error(), vpFeaturePointPolar::error(), vpFeatureThetaU::error(), vpFeatureTranslation::error(), vpBasicFeature::get_s(), vpFeatureEllipse::interaction(), vpFeatureVanishingPoint::interaction(), vpFeatureSegment::interaction(), vpGenericFeature::interaction(), vpFeatureMoment::interaction(), vpFeaturePoint::interaction(), vpFeatureLine::interaction(), vpFeaturePoint3D::interaction(), vpFeaturePointPolar::interaction(), vpFeatureThetaU::interaction(), vpFeatureTranslation::interaction(), and vpMatrix::stackMatrices().
Stack two Matrices C = [ A B ]^T.
Stack matrices. "Stack" two matrices C = [ A B ]^T.
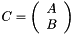
| A | : Upper matrix. |
| B | : Lower matrix. |
Definition at line 2581 of file vpMatrix.cpp.
References vpMatrix::stackMatrices(), and vpCERROR.
Stack two Matrices C = [ A B ]^T.
stackMatrices. "stack" two matrices C = [ A B ]^T
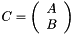
| A | : Upper matrix. |
| B | : Lower matrix. |
| C | : Stacked matrix C = [ A B ]^T |
Definition at line 2610 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpCERROR, and vpERROR_TRACE.
|
inherited |
Stacks rows of a matrix in a vector
| out | : a vpRowVector. |
Definition at line 1528 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::data, vpMatrix::dsize, vpRowVector::resize(), vpMatrix::rowNum, vpCERROR, and vpERROR_TRACE.
|
inherited |
Stacks rows of a matrix in a vector.
Definition at line 1550 of file vpMatrix.cpp.
References vpMatrix::colNum, and vpMatrix::rowNum.
|
staticinherited |
Operation C = A - B.
The result is placed in the third parameter C and not returned. A new matrix won't be allocated for every use of the function (Speed gain if used many times with the same result matrix size).
Definition at line 671 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::getCols(), vpMatrix::getRows(), vpMatrixException::incorrectMatrixSizeError, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, and vpERROR_TRACE.
Referenced by vpMatrix::operator-().
|
inherited |
Return the sum of all the 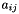 elements of the matrix.
elements of the matrix.
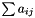
Definition at line 903 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
Referenced by vpMatrix::expm().
|
inherited |
Return the sum square of all the 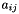 elements of the matrix.
elements of the matrix.
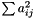
Definition at line 868 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::rowNum, and vpMatrix::rowPtrs.
Referenced by vpPose::calculArbreDementhon(), vpCalibration::calibrationTsai(), vpMbTracker::computeCovarianceMatrix(), vpPose::coplanar(), vpFeatureDepth::error(), vpFeatureThetaU::error(), vpFeatureTranslation::error(), vpMbTracker::extractCylinders(), vpFeatureThetaU::interaction(), vpMatrix::kernel(), vpRowVector::normalize(), vpColVector::normalize(), vpPose::poseDementhonNonPlan(), vpPose::poseDementhonPlan(), vpPose::poseFromRectangle(), vpPose::poseLagrangeNonPlan(), vpPose::poseLagrangePlan(), vpPose::poseVirtualVS(), vpPose::poseVirtualVSrobust(), vpMatrix::pseudoInverse(), vpServoData::save(), vpSimulatorAfma6::setPosition(), and vpSimulatorViper850::setPosition().
|
inherited |
Singular value decomposition (SVD).
![\[ M = U \Sigma V^{\top} \]](form_214.png)
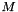 to decompose. You should make a COPY of that matrix if needed not to CHANGE.
to decompose. You should make a COPY of that matrix if needed not to CHANGE.| w | : Vector of singular values. 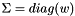 . . |
| v | : Matrix 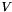 . . |
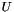 .
.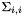 are ordered in decreasing fashion in w. This is not the case, if the GSL is not detected by ViSP.
are ordered in decreasing fashion in w. This is not the case, if the GSL is not detected by ViSP.Here an example of SVD decomposition of a non square Matrix M.
Definition at line 1822 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpColVector::resize(), and vpMatrix::resize().
Referenced by vpHomography::computeDisplacement(), vpMatrix::cond(), vpHomography::DLT(), vpMatrix::kernel(), vpPose::poseDementhonPlan(), and vpMatrix::pseudoInverse().
| vpRotationMatrix vpRotationMatrix::t | ( | ) | const |
transpose
transpose R^T
Definition at line 434 of file vpRotationMatrix.cpp.
Referenced by vpCalibration::calibrationTsai(), vpHomography::computeDisplacement(), vpVelocityTwistMatrix::extract(), vpVelocityTwistMatrix::inverse(), inverse(), vpHomogeneousMatrix::inverse(), isARotationMatrix(), and vpSimulatorAfma6::setPosition().
|
inherited |
Compute and return the transpose of the matrix.
Definition at line 1326 of file vpMatrix.cpp.
Referenced by vpTemplateTrackerWarpSRT::getParamInverse().
|
inherited |
Compute At the transpose of the matrix.
| At | : Resulting transpose matrix. |
Definition at line 1338 of file vpMatrix.cpp.
References vpMatrix::colNum, vpMatrix::resize(), vpMatrix::rowNum, vpMatrix::rowPtrs, vpCERROR, and vpERROR_TRACE.
Multiplication by a scalar Cij = x*Bij.
Definition at line 1006 of file vpMatrix.cpp.
References vpMatrix::getCols(), vpMatrix::getRows(), vpMatrix::resize(), and vpERROR_TRACE.
|
friend |
std::cout an rotation matrix [thetaU]
Definition at line 472 of file vpRotationMatrix.cpp.
|
related |
Compute the skew symmetric matrix 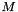 of translation vector
of translation vector 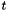 (matrice de pre-produit vectoriel).
(matrice de pre-produit vectoriel).
![\[ \mbox{if} \quad {\bf t} = \left( \begin{array}{c} t_x \\ t_y \\ t_z \end{array}\right), \quad \mbox{then} \qquad M = \left( \begin{array}{ccc} 0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0 \end{array}\right) \]](form_436.png)
| t | : Translation vector in input used to compute the skew symmetric matrix M. |
| M | : Skew symmetric matrix of translation vector 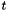 . . |
Definition at line 296 of file vpTranslationVector.cpp.
References vpMatrix::resize().
|
related |
This function performs generalized matrix multiplication: D = alpha*op(A)*op(B) + beta*op(C), where op(X) is X or X^T. Operation on A, B and C matrices is described by enumeration vpGEMMmethod.
For example, to compute alpha*A^T*B^T+beta*C we need to call :
If C is not used, vpGEMM must be called using an empty matrix null :
| vpMatrixException::incorrectMatrixSizeError | if the sizes of the matrices do not allow the operations. |
| A | : a Matrix |
| B | : a Matrix |
| alpha | : a scalar |
| C | : a Matrix |
| beta | : a scalar |
| D | : a Matrix |
| ops | : a scalar describing operation applied on the matrices |
Definition at line 331 of file vpGEMM.h.
References vpMatrixException::incorrectMatrixSizeError, and vpERROR_TRACE.
|
related |
Enumeration of the operations applied on matrices in vpGEMM function.
Operations are :
|
friend |
Definition at line 77 of file vpRotationMatrix.h.
|
friend |
Definition at line 76 of file vpRotationMatrix.h.
|
friend |
Definition at line 83 of file vpRotationMatrix.h.
|
friend |
Definition at line 78 of file vpRotationMatrix.h.
|
friend |
Definition at line 80 of file vpRotationMatrix.h.
|
friend |
Definition at line 79 of file vpRotationMatrix.h.
|
friend |
Definition at line 81 of file vpRotationMatrix.h.
|
friend |
Definition at line 82 of file vpRotationMatrix.h.
|
protectedinherited |
number of columns
Definition at line 114 of file vpMatrix.h.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::AtA(), vpMatrix::eigenValues(), vpMatrix::expm(), vpMatrix::eye(), vpMatrix::infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpMatrix::insert(), vpMatrix::inverseByCholesky(), vpMatrix::inverseByLU(), vpMatrix::inverseByQR(), vpMatrix::kron(), vpMatrix::mult2Matrices(), vpMatrix::multMatrixVector(), vpMatrix::negateMatrix(), vpRowVector::operator*(), vpMatrix::operator*(), vpMatrix::operator*=(), vpRowVector::operator+(), vpMatrix::operator+=(), vpRowVector::operator-(), vpMatrix::operator-=(), vpMatrix::operator/(), vpMatrix::operator/=(), vpColVector::operator<<(), vpMatrix::operator<<(), vpSubRowVector::operator=(), vpSubMatrix::operator=(), vpRowVector::operator=(), vpMatrix::operator=(), vpMatrix::resize(), vpMatrix::setIdentity(), vpMatrix::solveBySVD(), vpMatrix::stackColumns(), vpMatrix::stackRows(), vpMatrix::sub2Matrices(), vpMatrix::sum(), vpMatrix::sumSquare(), vpRowVector::t(), vpMatrix::t(), vpMatrix::transpose(), and vpMatrix::vpMatrix().
|
inherited |
address of the first element of the data array
Definition at line 118 of file vpMatrix.h.
Referenced by vpMatrix::AtA(), vpHomogeneousMatrix::buildFrom(), vpSubColVector::checkParentStatus(), vpSubRowVector::checkParentStatus(), vpSubMatrix::checkParentStatus(), vpPose::computeResidual(), vpPose::computeTransformation(), vpHomogeneousMatrix::convert(), vpColVector::dotProd(), vpMatrix::eigenValues(), vpMatrix::euclideanNorm(), vpMatrix::expm(), vpRobotViper650::getForceTorque(), vpRobotViper850::getForceTorque(), vpMatrix::getMaxValue(), vpMatrix::getMinValue(), vpRobotViper650::getPosition(), vpRobotViper850::getPosition(), vpRobotViper850::getVelocity(), vpRobotViper650::getVelocity(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpRobotViper650::init(), vpRobotViper850::init(), vpMatrix::inverseByCholeskyLapack(), vpMatrix::inverseByQRLapack(), vpColVector::invSort(), vpMatrix::kill(), vpColVector::mean(), vpColVector::median(), vpRowVector::operator*(), vpTranslationVector::operator*(), vpColVector::operator*(), vpTranslationVector::operator-(), vpColVector::operator-(), vpRowVector::operator-(), vpSubColVector::operator=(), vpSubRowVector::operator=(), vpRowVector::operator=(), vpColVector::operator=(), vpTranslationVector::operator=(), vpMatrix::operator=(), vpRowVector::operator[](), vpColVector::operator[](), vpPose::ransac(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::resize(), vpRobotAfma4::setPosition(), vpRobotViper650::setPosition(), vpRobotViper850::setPosition(), vpRobotAfma4::setVelocity(), vpRobotAfma6::setVelocity(), vpRobotViper650::setVelocity(), vpRobotViper850::setVelocity(), vpColVector::sort(), vpMatrix::stackColumns(), vpMatrix::stackRows(), vpRowVector::t(), vpColVector::t(), vpColVector::vpColVector(), vpMatrix::vpMatrix(), vpSubColVector::~vpSubColVector(), vpSubMatrix::~vpSubMatrix(), and vpSubRowVector::~vpSubRowVector().
|
protectedinherited |
Current size (rowNum * colNum)
Definition at line 124 of file vpMatrix.h.
Referenced by vpMatrix::euclideanNorm(), vpMatrix::getMaxValue(), vpMatrix::getMinValue(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpTranslationVector::operator*(), vpTranslationVector::operator-(), vpMatrix::operator=(), vpRowVector::reshape(), vpColVector::reshape(), vpMatrix::resize(), and vpMatrix::stackRows().
|
protectedinherited |
number of rows
Definition at line 112 of file vpMatrix.h.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::AtA(), vpColVector::deg2rad(), vpMatrix::eigenValues(), vpMatrix::expm(), vpMatrix::eye(), vpMatrix::infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpMatrix::insert(), vpMatrix::inverseByCholesky(), vpMatrix::inverseByLU(), vpMatrix::inverseByQR(), vpMatrix::kron(), vpMatrix::mult2Matrices(), vpMatrix::multMatrixVector(), vpMatrix::negateMatrix(), vpColVector::operator*(), vpHomogeneousMatrix::operator*(), vpMatrix::operator*(), vpMatrix::operator*=(), vpColVector::operator+(), vpMatrix::operator+=(), vpColVector::operator-(), vpMatrix::operator-=(), vpMatrix::operator/(), vpMatrix::operator/=(), vpColVector::operator<<(), vpMatrix::operator<<(), vpSubColVector::operator=(), vpSubRowVector::operator=(), vpSubMatrix::operator=(), vpRowVector::operator=(), vpColVector::operator=(), vpTranslationVector::operator=(), vpMatrix::operator=(), vpColVector::rad2deg(), vpMatrix::resize(), vpMatrix::setIdentity(), vpColVector::stack(), vpMatrix::stackColumns(), vpMatrix::stackMatrices(), vpMatrix::stackRows(), vpMatrix::sub2Matrices(), vpMatrix::sum(), vpMatrix::sumSquare(), vpColVector::t(), vpMatrix::t(), vpMatrix::transpose(), and vpMatrix::vpMatrix().
|
protectedinherited |
address of the first element of each rows
Definition at line 121 of file vpMatrix.h.
Referenced by vpMatrix::AAt(), vpMatrix::add2Matrices(), vpMatrix::add2WeightedMatrices(), vpMatrix::infinityNorm(), vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), vpMatrix::kill(), vpMatrix::mult2Matrices(), vpMatrix::multMatrixVector(), vpMatrix::negateMatrix(), operator*(), vpVelocityTwistMatrix::operator*(), vpForceTwistMatrix::operator*(), vpHomogeneousMatrix::operator*(), vpMatrix::operator*(), vpMatrix::operator*=(), vpMatrix::operator+=(), vpMatrix::operator-=(), vpMatrix::operator/(), vpMatrix::operator/=(), vpColVector::operator<<(), vpMatrix::operator<<(), vpSubMatrix::operator=(), vpRowVector::operator=(), operator=(), vpVelocityTwistMatrix::operator=(), vpForceTwistMatrix::operator=(), vpHomogeneousMatrix::operator=(), vpMatrix::operator=(), vpMatrix::resize(), vpMatrix::stackColumns(), vpMatrix::sub2Matrices(), vpMatrix::sum(), vpMatrix::sumSquare(), and vpMatrix::transpose().
|
protectedinherited |
Total row space.
Definition at line 126 of file vpMatrix.h.
Referenced by vpSubColVector::init(), vpSubRowVector::init(), vpSubMatrix::init(), vpMatrix::init(), and vpMatrix::resize().