 |
Visual Servoing Platform
version 3.6.1 under development (2025-02-28)
|
 |
Visual Servoing Platform
version 3.6.1 under development (2025-02-28)
|
#include <visp3/core/vpBSpline.h>
 Inheritance diagram for vpBSpline:
Inheritance diagram for vpBSpline:Public Member Functions | |
| vpBSpline () | |
| vpBSpline (const vpBSpline &bspline) | |
| virtual | ~vpBSpline () |
| unsigned int | get_p () const |
| void | get_controlPoints (std::list< vpImagePoint > &list) const |
| void | get_knots (std::list< double > &list) const |
| void | get_crossingPoints (std::list< vpImagePoint > &list) const |
| void | set_p (unsigned int degree) |
| void | set_controlPoints (const std::list< vpImagePoint > &list) |
| void | set_knots (const std::list< double > &list) |
| void | set_crossingPoints (const std::list< vpImagePoint > &list) |
| unsigned int | findSpan (double u) const |
| vpBasisFunction * | computeBasisFuns (double u) const |
| vpBasisFunction ** | computeDersBasisFuns (double u, unsigned int der) const |
| vpImagePoint | computeCurvePoint (double u) const |
| vpImagePoint * | computeCurveDers (double u, unsigned int der) const |
Static Public Member Functions | |
| static unsigned int | findSpan (double l_u, unsigned int l_p, const std::vector< double > &l_knots) |
| static vpBasisFunction * | computeBasisFuns (double l_u, unsigned int l_i, unsigned int l_p, const std::vector< double > &l_knots) |
| static vpBasisFunction ** | computeDersBasisFuns (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, const std::vector< double > &l_knots) |
| static vpImagePoint | computeCurvePoint (double l_u, unsigned int l_i, unsigned int l_p, const std::vector< double > &l_knots, const std::vector< vpImagePoint > &l_controlPoints) |
| static vpImagePoint * | computeCurveDers (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, const std::vector< double > &l_knots, const std::vector< vpImagePoint > &l_controlPoints) |
Class that provides tools to compute and manipulate a B-Spline curve.
The different parameters are :
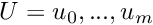 where the knots
where the knots 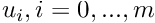 are real number such as
are real number such as 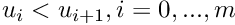 . To define a curve, the knot vector is such as :
. To define a curve, the knot vector is such as : 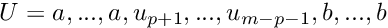 where
where 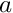 and
and 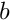 are real numbers and p is the degree of the B-Spline basis functions.
are real numbers and p is the degree of the B-Spline basis functions.The B-Spline basis functions 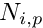 defined as :
defined as :
![\[ N_{i,0}(u) = \left\{\begin{array}{cc} 1 & \mbox{if } u_i \leq u \leq u_{i+1} \\ 0 & else \end{array}\right.\]](form_10.png)
![\[ N_{i,p}(u) = \frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)\]](form_11.png)
where 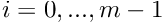 and p is the degree of the B-Spline basis functions.
and p is the degree of the B-Spline basis functions.
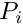 which are defined by the coordinates
which are defined by the coordinates  of a point in an image.
of a point in an image.It is possible to compute the coordinates of a point corresponding to the knots 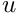 (
( ![$ u \in [u_0,u_m]$](form_16.png) ) thanks to the formula :
) thanks to the formula :
![\[ C(u) = \sum_{i=0}^n (N_{i,p}(u)P_i)\]](form_17.png)
You can find much more information about the B-Splines and the implementation of all the methods in the Nurbs Book.
Definition at line 107 of file vpBSpline.h.
| BEGIN_VISP_NAMESPACE vpBSpline::vpBSpline | ( | ) |
Basic constructor.
The degree ![]() of the B-Spline basis functions is set to 3 to compute cubic B-Spline.
of the B-Spline basis functions is set to 3 to compute cubic B-Spline.
Definition at line 46 of file vpBSpline.cpp.
| vpBSpline::vpBSpline | ( | const vpBSpline & | bspline | ) |
Copy constructor.
Definition at line 55 of file vpBSpline.cpp.
|
virtual |
Basic destructor.
Definition at line 62 of file vpBSpline.cpp.
|
static |
Compute the nonvanishing basis functions at ![]() which is in the
which is in the ![]() th knot interval. All the basis functions are stored in an array such as :
th knot interval. All the basis functions are stored in an array such as :
N = ![]() ,
, ![]() ,
, ![]() , ... ,
, ... , ![]() , ...,
, ..., ![]() , ... ,
, ... , ![]() , ... ,
, ... , ![]()
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
Definition at line 143 of file vpBSpline.cpp.
Referenced by computeBasisFuns(), computeCurvePoint(), vpNurbs::computeCurvePoint(), vpNurbs::globalCurveApprox(), and vpNurbs::globalCurveInterp().
| vpBasisFunction * vpBSpline::computeBasisFuns | ( | double | u | ) | const |
Compute the nonvanishing basis functions at 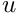 . All the basis functions are stored in an array such as :
. All the basis functions are stored in an array such as :
N = ![]() ,
, ![]() ,
, ![]() , ... ,
, ... , ![]() , ...,
, ..., ![]() , ... ,
, ... , ![]() , ... ,
, ... , ![]()
where i the number of the knot interval in which 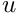 lies.
lies.
| u | : A real number which is between the extremities of the knot vector |
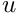 . The size of the array is
. The size of the array is Definition at line 194 of file vpBSpline.cpp.
References computeBasisFuns(), and findSpan().
|
static |
Compute the kth derivatives of ![]() for
for ![]() .
.
The formula used is the following :
![]()
where 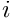 is the knot interval number in which
is the knot interval number in which 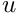 lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
Definition at line 446 of file vpBSpline.cpp.
References computeDersBasisFuns(), vpImagePoint::set_i(), vpImagePoint::set_ij(), and vpImagePoint::set_j().
| vpImagePoint * vpBSpline::computeCurveDers | ( | double | u, |
| unsigned int | der | ||
| ) | const |
Compute the kth derivatives of ![]() for
for ![]() .
.
The formula used is the following :
![]()
where 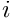 is the knot interval number in which
is the knot interval number in which 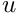 lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| u | : A real number which is between the extremities of the knot vector |
| der | : The last derivative to be computed. |
Definition at line 493 of file vpBSpline.cpp.
References computeDersBasisFuns(), vpImagePoint::set_i(), vpImagePoint::set_ij(), and vpImagePoint::set_j().
|
static |
Compute the coordinates of a point ![]() corresponding to the knot
corresponding to the knot 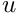 .
.
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
return the coordinates of a point corresponding to the knot 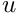 .
.
Definition at line 376 of file vpBSpline.cpp.
References computeBasisFuns(), vpImagePoint::set_i(), and vpImagePoint::set_j().
| vpImagePoint vpBSpline::computeCurvePoint | ( | double | u | ) | const |
Compute the coordinates of a point ![]() corresponding to the knot
corresponding to the knot 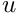 .
.
| u | : A real number which is between the extremities of the knot vector |
return the coordinates of a point corresponding to the knot 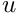 .
.
Definition at line 405 of file vpBSpline.cpp.
References computeBasisFuns(), vpImagePoint::set_i(), and vpImagePoint::set_j().
|
static |
Compute the nonzero basis functions and their derivatives until the ![]() th derivative. All the functions are computed at l_u.
th derivative. All the functions are computed at l_u.
The result is given as an array of size l_der+1 x l_p+1. The kth line corresponds to the kth basis functions derivatives.
The formula to compute the kth derivative at 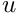 is :
is :
![]()
where 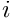 is the knot interval number in which
is the knot interval number in which 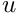 lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector |
Example : return[0] is the list of the 0th derivatives ie the basis functions. return[k] is the list of the kth derivatives.
Definition at line 229 of file vpBSpline.cpp.
Referenced by computeCurveDers(), vpNurbs::computeCurveDers(), and computeDersBasisFuns().
| vpBasisFunction ** vpBSpline::computeDersBasisFuns | ( | double | u, |
| unsigned int | der | ||
| ) | const |
Compute the nonzero basis functions and their derivatives until the ![]() th derivative. All the functions are computed at u.
th derivative. All the functions are computed at u.
The result is given as an array of size der+1 x p+1. The kth line corresponds to the kth basis functions derivatives.
The formula to compute the kth derivative at 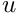 is :
is :
![]()
where 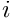 is the knot interval number in which
is the knot interval number in which 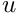 lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| u | : A real number which is between the extremities of the knot vector |
| der | : The last derivative to be computed. |
Example : return[0] is the list of the 0th derivatives ie the basis functions. return[k] is the list of the kth derivatives.
Definition at line 359 of file vpBSpline.cpp.
References computeDersBasisFuns(), and findSpan().
|
static |
Find the knot interval in which the parameter ![]() lies. Indeed
lies. Indeed ![]()
Example : The knot vector is the following ![]() with
with ![]() is equal to 1.
is equal to 1.
| l_u | : The knot whose knot interval is seeked. |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
Definition at line 80 of file vpBSpline.cpp.
References vpMath::maximum(), and vpMath::round().
Referenced by computeBasisFuns(), vpNurbs::computeCurveDersPoint(), computeDersBasisFuns(), vpNurbs::curveKnotIns(), findSpan(), vpNurbs::globalCurveApprox(), vpNurbs::globalCurveInterp(), and vpNurbs::refineKnotVectCurve().
| unsigned int vpBSpline::findSpan | ( | double | u | ) | const |
Find the knot interval in which the parameter 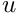 lies. Indeed
lies. Indeed ![]()
Example : The knot vector is the following ![]() with
with ![]() is equal to 1.
is equal to 1.
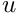 equal to 0.5 the method will return 1.
equal to 0.5 the method will return 1.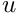 equal to 2.5 the method will return 3.
equal to 2.5 the method will return 3.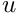 equal to 3 the method will return 3.
equal to 3 the method will return 3.| u | : The knot whose knot interval is seeked. |
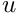 lies.
lies. Definition at line 124 of file vpBSpline.cpp.
References findSpan().
|
inline |
Gets all the control points.
| list | : A std::list containing the coordinates of the control points. |
Definition at line 137 of file vpBSpline.h.
|
inline |
Gets all the crossing points (used in the interpolation method)
| list | : A std::list containing the coordinates of the crossing points. |
Definition at line 164 of file vpBSpline.h.
|
inline |
Gets all the knots.
| list | : A std::list containing the value of the knots. |
Definition at line 150 of file vpBSpline.h.
|
inline |
Gets the degree of the B-Spline.
Definition at line 129 of file vpBSpline.h.
|
inline |
Sets all the control points.
| list | : A std::list containing the coordinates of the control points |
Definition at line 184 of file vpBSpline.h.
|
inline |
Sets all the crossing points (used in the interpolation method)
| list | : A std::list containing the coordinates of the crossing points |
Definition at line 211 of file vpBSpline.h.
|
inline |
Sets all the knots.
| list | : A std::list containing the value of the knots. |
Definition at line 197 of file vpBSpline.h.
|
inline |
Sets the degree of the B-Spline.
| degree | : the degree of the B-Spline. |
Definition at line 177 of file vpBSpline.h.