Visual Servoing Platform  version 3.4.0
Tutorial: Template tracking

Table of Contents

Introduction

With ViSP it is possible to track a template using image registration algorithms [10] [11]. Contrary to common approaches based on visual features, this method allows to be much more robust to scene variations.

In the following sections, we consider the tracking of a pattern. To simplify the source code, the tracking is performed on a single image. The extension to a sequence of images or to images acquired from a camera is easy. To this end see Tutorial: Image frame grabbing.

Note that all the material (source code and video) described in this tutorial is part of ViSP source code and could be downloaded using the following command:

$ svn export https://github.com/lagadic/visp.git/trunk/tutorial/tracking/template-tracker

Track the painting

The following example that comes from tutorial-template-tracker.cpp allows to track a template using vpTemplateTrackerSSDInverseCompositional class. Let us denote that "SSDInverseCompositional" refers to the similarity function used for the image registration. In ViSP, we have implemented, for now, three different similarity functions: the "Sum of Square Differences" (vpTemplateTrackerSSD classes [1]), the "Zero-mean Normalized Cross Correlation" (vpTemplateTrackerZNCC classes [19]) and the "Mutual Information" (vpTemplateTrackerMI classes [10]). All the methods can be used in different ways: Inverse Compositional, Forward Compositional, Forward Additional, or ESM.

As detailed in Warping classes section, the tracker is able to track a reference template (in our case a painting) and to estimate the transformation between the reference template and its current position. The estimated transformationn could be modeled as:

#include <visp3/gui/vpDisplayGDI.h>
#include <visp3/gui/vpDisplayOpenCV.h>
#include <visp3/gui/vpDisplayX.h>
#include <visp3/io/vpVideoReader.h>
#include <visp3/tt/vpTemplateTrackerSSDInverseCompositional.h>
#include <visp3/tt/vpTemplateTrackerWarpHomography.h>
int main(int argc, char **argv)
{
#if defined(VISP_HAVE_OPENCV) && (VISP_HAVE_OPENCV_VERSION >= 0x020100)
std::string opt_videoname = "bruegel.mp4";
unsigned int opt_subsample = 1;
for (int i = 0; i < argc; i++) {
if (std::string(argv[i]) == "--videoname")
opt_videoname = std::string(argv[i + 1]);
else if (std::string(argv[i]) == "--subsample")
opt_subsample = static_cast<unsigned int>(std::atoi(argv[i + 1]));
else if (std::string(argv[i]) == "--help" || std::string(argv[i]) == "-h") {
std::cout << "\nUsage: " << argv[0] << " [--videoname <video name>] [--subsample <scale factor>] [--help] [-h]\n" << std::endl;
return 0;
}
}
std::cout << "Video name: " << opt_videoname << std::endl;
vpImage<unsigned char> I, Iacq;
vpVideoReader g;
g.setFileName(opt_videoname);
g.open(Iacq);
Iacq.subsample(opt_subsample, opt_subsample, I);
#if defined(VISP_HAVE_X11)
vpDisplayX display;
#elif defined(VISP_HAVE_GDI)
vpDisplayGDI display;
#elif defined(VISP_HAVE_OPENCV)
vpDisplayOpenCV display;
#else
std::cout << "No image viewer is available..." << std::endl;
#endif
display.setDownScalingFactor(vpDisplay::SCALE_AUTO);
display.init(I, 100, 100, "Template tracker");
vpDisplay::display(I);
vpDisplay::flush(I);
vpTemplateTrackerWarpHomography warp;
vpTemplateTrackerSSDInverseCompositional tracker(&warp);
tracker.setSampling(2, 2);
tracker.setLambda(0.001);
tracker.setIterationMax(200);
tracker.setPyramidal(2, 1);
tracker.initClick(I);
while (1) {
double t = vpTime::measureTimeMs();
g.acquire(Iacq);
Iacq.subsample(opt_subsample, opt_subsample, I);
vpDisplay::display(I);
tracker.track(I);
vpColVector p = tracker.getp();
vpHomography H = warp.getHomography(p);
std::cout << "Homography: \n" << H << std::endl;
tracker.display(I, vpColor::red);
vpDisplay::displayText(I, 10*vpDisplay::getDownScalingFactor(I), 10*vpDisplay::getDownScalingFactor(I),
"Click to quit", vpColor::red);
if (vpDisplay::getClick(I, false))
break;
vpDisplay::flush(I);
if (! g.isVideoFormat()) {
vpTime::wait(t, 40);
}
}
#else
(void)argc;
(void)argv;
#endif
}

The video below shows the result of the template tracking.

Hereafter is the description of the new lines introduced in this example.

#include <visp3/tt/vpTemplateTrackerSSDInverseCompositional.h>
#include <visp3/tt/vpTemplateTrackerWarpHomography.h>

Here we include the header of the vpTemplateTrackerSSDInverseCompositional class that allows to track the template. Actually, the tracker estimates the displacement of the template in the current image according to its initial pose. The computed displacement can be represented by multiple transformations, also called warps (vpTemplateTrackerWarp classes). In this example, we include the header vpTemplateTrackerWarpHomography class to define the possible transformation of the template as an homography.

vpTemplateTrackerWarpHomography warp;
vpTemplateTrackerSSDInverseCompositional tracker(&warp);

Once the tracker is created with the desired warp function, parameters can be tuned to be more consistent with the expected behavior. Depending on these parameters the perfomances of the tracker in terms of processing time and estimation could be affected. Since here we deal with 640 by 480 pixel wide images, the images are significantly subsampled in order to reduce the time of the image processing to be compatible with real-time.

tracker.setSampling(2, 2); // Will consider only one pixel from two along rows and columns
// to create the reference template
tracker.setLambda(0.001); // Gain used in the optimization loop
tracker.setIterationMax(200); // Maximum number of iterations for the optimization loop
tracker.setPyramidal(2, 1); // First and last level of the pyramid. Full resolution image is at level 0.

The last step of the initialization is to select the template that will be tracked during the sequence.

tracker.initClick(I);

The vpTemplateTracker classes proposed in ViSP offer you the possibility to defined your template as multiple planar triangles. When calling the previous line, you will have to specify the triangles that define the template.

img-initClickTemplateTracker.png
Initialization of the template without Delaunay triangulation.

Let us denote that those triangles don't have to be spatially tied up. However, if you want to track a simple image as in this example, you should initialize the template as on the figure above. Left clicks on point number zero, one and two create the green triangle. Left clicks on point three and four and then right click on point number five create the red triangle and ends the initialization. If ViSP is build with OpenCV, we also provide an initialization with automatic triangulation using Delaunay. To use it, you just have to call vpTemplateTracker::initClick(I, true). Then by left clicking on points number zero, one, two, four and right clicking on point number five initializes the tracker as on the image above.

Next, in the infinite while loop, after displaying the next image, we track the object on a new image I.

tracker.track(I);

If you need to get the parameters of the current transformation of the template, it can be done by calling:

vpColVector p = tracker.getp();
vpHomography H = warp.getHomography(p);
std::cout << "Homography: \n" << H << std::endl;

For further information about the warping parameters, see the following Warping classes section.

Then according to the computed transformation obtained from the last call to track() function, next line is used to display the template using red lines.

tracker.display(I, vpColor::red);

Warping classes

In the example presented above, we focused on the vpTemplateTrackerWarpHomography warping class which is the most generic transformation available in ViSP for the template trackers. However, if you know that the template you want to track is constrained, other warps might be more suitable.

vpTemplateTrackerWarpTranslation

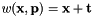$w({\bf x},{\bf p}) = {\bf x} + {\bf t}$ with the following estimated parameters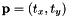 $ {\bf p} = (t_x, t_y)$

This class is the most simple transformation available for the template trackers. It only considers translation on two-axis (x-axis and y-axis).

vpTemplateTrackerWarpSRT

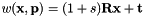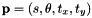
$w({\bf x},{\bf p}) = (1+s){\bf Rx} + {\bf t}$ with ${\bf p} = (s, \theta, t_x, t_y)$

The SRT warp considers a scale factor, a rotation on z-axis and a 2D translation as in vpTemplateTrackerWarpTranslation.

vpTemplateTrackerWarpAffine

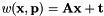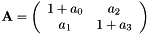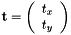$ w({\bf x},{\bf p}) = {\bf Ax} + {\bf t}$ with ${\bf A} = \left( \begin{array}{cc} 1+a_0 & a_2 \\ a_1 & 1+a_3 \end{array} \right)$, ${\bf t} = \left( \begin{array}{c} t_x \\ t_y \end{array} \right)$ and the estimated parameters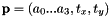 ${\bf p} = (a_0 ... a_3, t_x, t_y)$

The template transformation can also be defined as an affine transformation. This warping function preserves points, straight lines, and planes.

vpTemplateTrackerWarpHomography

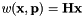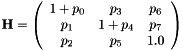$w({\bf x},{\bf p}) = {\bf Hx}$ with $ {\bf H}=\left( \begin{array}{ccc} 1 + p_0 & p_3 & p_6 \\ p_1 & 1+p_4 & p_7 \\ p_2 & p_5 & 1.0 \end{array} \right) $ and the estimated parameters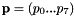 ${\bf p} = (p_0 ... p_7)$

As remind, the vpTemplateTrackerWarpHomography estimates the eight parameters of the homography matrix 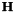$ {\bf H}$.

vpTemplateTrackerWarpHomographySL3

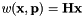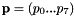
$w({\bf x},{\bf p}) = {\bf Hx}$ with ${\bf p} = (p_0 ... p_7)$

The vpTemplateTrackerWarpHomographySL3 warp works exactly the same as the vpTemplateTrackerWarpHomography warp. The only difference is that here, the parameters of the homography are estimated in the SL3 reference frame.

How to tune the tracker

When you want to obtain a perfect pose estimation, it is often time-consuming. However, by tuning the tracker, you can find a good compromise between speed and efficiency. Basically, what will make the difference is the size of the reference template. The more pixels it contains, the more time-consuming it will be. Fortunately, the solutions to avoid this problem are multiple. First of all lets come back on the vpTemplateTracker::setSampling() function.

tracker.setSampling(4, 4); // Will consider only one pixel from four along rows and columns
// to create the reference template.

In the example above, we decided to consider only one pixel from 16 (4 by 4) to create the reference template. Obviously, by increasing those values it will consider much less pixels, which unfortunately decrease the efficiency, but the tracking phase will be much faster.

The tracking phase relies on an iterative algorithm minimizing a cost function. What does it mean? It means this algorithm has, at some point, to stop! Once again, you have the possibility to reduce the number of iterations of the algorithm by taking the risk to fall in a local minimum.

tracker.setIterationMax(50); // Maximum number of iterations for the optimization loop.

If this is still not enough for you, let's remember that all of our trackers can be used in a pyramidal way. By reducing the number of levels considered by the algorithm, you will consider, once again, much less pixels and be faster.

tracker.setPyramidal(3, 2); // First and last level of the pyramid

Note here that when vpTemplateTracker::setPyramidal() function is not used, the pyramidal approach to speed up the algorithm is not used.

Let us denote that if you're using vpTemplateTrackerSSDInverseCompositional or vpTemplateTrackerZNCCInverseCompositional, you also have another interesting option to speed up your tracking phase.

tracker.setUseTemplateSelect(true);

This function will force the tracker to only consider, in the reference template, the pixels that have an high gradient value. This is another solution to limit the number of considered pixels.

As well as vpTemplateTrackerSSDInverseCompositional::setUseTemplateSelect() or vpTemplateTrackerMIInverseCompositional::setUseTemplateSelect(), another function, only available in vpTemplateTrackerSSDInverseCompositional and vpTemplateTrackerZNCCInverseCompositional is:

tracker.setThresholdRMS(1e-6);

By increasing this root mean square threshold value, the algorithm will reduce its number of iterations which should also speed up the tracking phase. This function should be used wisely with the vpTemplateTracker::setIterationMax() function.

Example tuning MI tracker

In tutorial-template-tracker.cpp we use vpTemplateTrackerSSDInverseCompositional class that implements the "Sum of Square Differences" as similarity function. To use Mutual Information that is more robust to occlusion and lighting changes, the code needs to be modified, first introducing vpTemplateTrackerMIInverseCompositional header, then instanciating the tracker, and finally setting the paramaters to speed up the MI tracker that is slower than the SSD one:

How to get the points of the template

The previous code provided in tutorial-template-tracker.cpp can be modified to get the coordinates of the corners of the triangles that define the zone to track. To this end, as shown in the next lines, before the while loop we first define a reference zone and the corresponding warped zone. Then in the loop, we update the warped zone using the parameters of the warping model that is estimated by the tracker. From the warped zone, we extract all the triangles, and then for each triangles, we get the corners coordinates.

// Instantiate and get the reference zone
vpTemplateTrackerZone zone_ref = tracker.getZoneRef();
// Instantiate a warped zone
vpTemplateTrackerZone zone_warped;
while(!g.end()){
g.acquire(I);
vpDisplay::display(I);
tracker.track(I);
tracker.display(I, vpColor::red);
// Get the estimated parameters
vpColVector p = tracker.getp();
// Update the warped zone given the tracker estimated parameters
warp.warpZone(zone_ref, p, zone_warped);
// Parse all the triangles that describe the zone
for (int i=0; i < zone_warped.getNbTriangle(); i++) {
vpTemplateTrackerTriangle triangle;
// Get a triangle
zone_warped.getTriangle(i, triangle);
std::vector<vpImagePoint> corners;
// Get the 3 triangle corners
triangle.getCorners( corners );
// From here, each corner triangle is available in
// corners[0], corners[1] and corners[2]
// Display a green cross over each corner
for(unsigned int j=0; j<corners.size(); j++)
vpDisplay::displayCross(I, corners[j], 15, vpColor::green, 2);
}
vpDisplay::displayRectangle(I, zone_warped.getBoundingBox(), vpColor::orange);

With the last line, we also sho how to get and display an orange rectangle that corresponds to the bounding box of all the triangles that define the zone.

The resulting drawings introduced previously are shown in the next image. Here we initialize the tracker with 2 triangles that are not connex.

img-template-tracker.jpg

More examples

The templateTracker.cpp source code provided in the example/tracking folder allows to test all the template tracker classes that derive from vpTemplateTracker as well as all the warping classes that derive from vpTemplateTrackerWarp.

Once build, in a terminal just run:

./templateTracker -h

to see which are the command lines options.