 |
Visual Servoing Platform
version 3.1.0
|
 |
Visual Servoing Platform
version 3.1.0
|
#include <visp3/core/vpBSpline.h>
 Inheritance diagram for vpBSpline:
Inheritance diagram for vpBSpline:Public Member Functions | |
| vpBSpline () | |
| vpBSpline (const vpBSpline &bspline) | |
| virtual | ~vpBSpline () |
| unsigned int | get_p () const |
| void | get_controlPoints (std::list< vpImagePoint > &list) const |
| void | get_knots (std::list< double > &list) const |
| void | get_crossingPoints (std::list< vpImagePoint > &list) const |
| void | set_p (unsigned int degree) |
| void | set_controlPoints (const std::list< vpImagePoint > &list) |
| void | set_knots (const std::list< double > &list) |
| void | set_crossingPoints (const std::list< vpImagePoint > &list) |
| unsigned int | findSpan (double u) |
| vpBasisFunction * | computeBasisFuns (double u) |
| vpBasisFunction ** | computeDersBasisFuns (double u, unsigned int der) |
| vpImagePoint | computeCurvePoint (double u) |
| vpImagePoint * | computeCurveDers (double u, unsigned int der) |
Static Public Member Functions | |
| static unsigned int | findSpan (double l_u, unsigned int l_p, std::vector< double > &l_knots) |
| static vpBasisFunction * | computeBasisFuns (double l_u, unsigned int l_i, unsigned int l_p, std::vector< double > &l_knots) |
| static vpBasisFunction ** | computeDersBasisFuns (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, std::vector< double > &l_knots) |
| static vpImagePoint | computeCurvePoint (double l_u, unsigned int l_i, unsigned int l_p, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints) |
| static vpImagePoint * | computeCurveDers (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints) |
Class that provides tools to compute and manipulate a B-Spline curve.
The different parameters are :
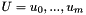 where the knots
where the knots 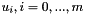 are real number such as
are real number such as 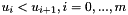 . To define a curve, the knot vector is such as :
. To define a curve, the knot vector is such as : 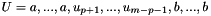 where
where 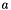 and
and 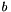 are real numbers and p is the degree of the B-Spline basis functions.
are real numbers and p is the degree of the B-Spline basis functions.The B-Spline basis functions 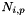 defined as :
defined as :
![\[ N_{i,0}(u) = \left\{\begin{array}{cc} 1 & \mbox{if } u_i \leq u \leq u_{i+1} \\ 0 & else \end{array}\right.\]](form_10.png)
![\[ N_{i,p}(u) = \frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)\]](form_11.png)
where 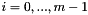 and p is the degree of the B-Spline basis functions.
and p is the degree of the B-Spline basis functions.
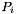 which are defined by the coordinates
which are defined by the coordinates 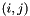 of a point in an image.
of a point in an image.It is possible to compute the coordinates of a point corresponding to the knots 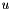 (
( ![$ u \in [u_0,u_m]$](form_16.png) ) thanks to the formula :
) thanks to the formula :
![\[ C(u) = \sum_{i=0}^n (N_{i,p}(u)P_i)\]](form_17.png)
You can find much more information about the B-Splines and the implementation of all the methods in the Nurbs Book.
Definition at line 110 of file vpBSpline.h.
| vpBSpline::vpBSpline | ( | ) |
Basic constructor.
The degree 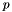 of the B-Spline basis functions is set to 3 to compute cubic B-Spline.
of the B-Spline basis functions is set to 3 to compute cubic B-Spline.
Definition at line 48 of file vpBSpline.cpp.
| vpBSpline::vpBSpline | ( | const vpBSpline & | bspline | ) |
Copy constructor.
Definition at line 58 of file vpBSpline.cpp.
|
virtual |
Basic destructor.
Definition at line 66 of file vpBSpline.cpp.
|
static |
Compute the nonvanishing basis functions at 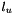 which is in the
which is in the 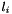 th knot interval. All the basis functions are stored in an array such as :
th knot interval. All the basis functions are stored in an array such as :
N = 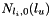 ,
, 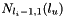 ,
, 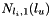 , ... ,
, ... , 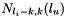 , ...,
, ..., 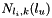 , ... ,
, ... , 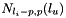 , ... ,
, ... , 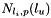
| l_u | : A real number which is between the extrimities of the knot vector |
| l_i | : the number of the knot interval in which 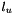 lies lies |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
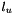 . The size of the array is
. The size of the array is 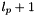 .
. Definition at line 148 of file vpBSpline.cpp.
Referenced by computeBasisFuns(), vpNurbs::computeCurvePoint(), computeCurvePoint(), vpNurbs::globalCurveApprox(), and vpNurbs::globalCurveInterp().
| vpBasisFunction * vpBSpline::computeBasisFuns | ( | double | u | ) |
Compute the nonvanishing basis functions at 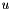 . All the basis functions are stored in an array such as :
. All the basis functions are stored in an array such as :
N = 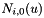 ,
, 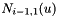 ,
, 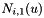 , ... ,
, ... , 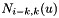 , ...,
, ..., 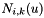 , ... ,
, ... , 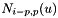 , ... ,
, ... , 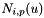
where i the number of the knot interval in which 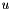 lies.
lies.
| u | : A real number which is between the extrimities of the knot vector |
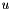 . The size of the array is
. The size of the array is 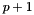 .
. Definition at line 199 of file vpBSpline.cpp.
References computeBasisFuns(), and findSpan().
|
static |
Compute the kth derivatives of 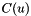 for
for 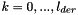 .
.
The formula used is the following :
![\[ C^{(k)}(u) = \sum_{i=0}^n (N_{i,p}^{(k)}(u)P_i) \]](form_469.png)
where 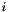 is the knot interval number in which
is the knot interval number in which 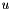 lies and
lies and 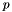 is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| l_u | : A real number which is between the extrimities of the knot vector |
| l_i | : the number of the knot interval in which 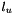 lies lies |
| l_p | : Degree of the B-Spline basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
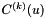 for
for 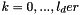 . The kth derivative is in the kth cell of the array.
. The kth derivative is in the kth cell of the array. Definition at line 451 of file vpBSpline.cpp.
References computeDersBasisFuns(), vpImagePoint::set_i(), vpImagePoint::set_ij(), vpImagePoint::set_j(), and vpTRACE.
| vpImagePoint * vpBSpline::computeCurveDers | ( | double | u, |
| unsigned int | der | ||
| ) |
Compute the kth derivatives of 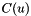 for
for 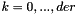 .
.
The formula used is the following :
![\[ C^{(k)}(u) = \sum_{i=0}^n (N_{i,p}^{(k)}(u)P_i) \]](form_469.png)
where 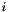 is the knot interval number in which
is the knot interval number in which 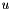 lies and
lies and 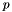 is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| u | : A real number which is between the extrimities of the knot vector |
| der | : The last derivative to be computed. |
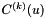 for
for 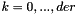 . The kth derivative is in the kth cell of the array.
. The kth derivative is in the kth cell of the array. Definition at line 497 of file vpBSpline.cpp.
References computeDersBasisFuns(), vpImagePoint::set_i(), vpImagePoint::set_ij(), vpImagePoint::set_j(), and vpTRACE.
|
static |
Compute the coordinates of a point 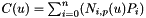 corresponding to the knot
corresponding to the knot 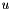 .
.
| l_u | : A real number which is between the extrimities of the knot vector |
| l_i | : the number of the knot interval in which 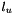 lies lies |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
return the coordinates of a point corresponding to the knot 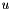 .
.
Definition at line 381 of file vpBSpline.cpp.
References computeBasisFuns(), vpImagePoint::set_i(), and vpImagePoint::set_j().
Referenced by vpNurbs::set_weights().
| vpImagePoint vpBSpline::computeCurvePoint | ( | double | u | ) |
Compute the coordinates of a point 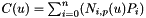 corresponding to the knot
corresponding to the knot 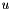 .
.
| u | : A real number which is between the extrimities of the knot vector |
return the coordinates of a point corresponding to the knot 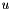 .
.
Definition at line 410 of file vpBSpline.cpp.
References computeBasisFuns(), vpImagePoint::set_i(), and vpImagePoint::set_j().
|
static |
Compute the nonzero basis functions and their derivatives until the 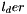 th derivative. All the functions are computed at l_u.
th derivative. All the functions are computed at l_u.
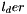 must be under or equal
must be under or equal 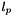 .
.The result is given as an array of size l_der+1 x l_p+1. The kth line corresponds to the kth basis functions derivatives.
The formula to compute the kth derivative at 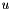 is :
is :
![\[ N_{i,p}^{(k)}(u) =p \left( \frac{N_{i,p-1}^{(k-1)}}{u_{i+p}-u_i} - \frac{N_{i+1,p-1}^{(k-1)}}{u_{i+p+1}-u_{i+1}} \right) \]](form_464.png)
where 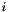 is the knot interval number in which
is the knot interval number in which 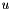 lies and
lies and 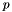 is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| l_u | : A real number which is between the extrimities of the knot vector |
| l_i | : the number of the knot interval in which 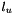 lies lies |
| l_p | : Degree of the B-Spline basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector |
Example : return[0] is the list of the 0th derivatives ie the basis functions. return[k] is the list of the kth derivatives.
Definition at line 234 of file vpBSpline.cpp.
References vpTRACE.
Referenced by vpNurbs::computeCurveDers(), computeCurveDers(), and computeDersBasisFuns().
| vpBasisFunction ** vpBSpline::computeDersBasisFuns | ( | double | u, |
| unsigned int | der | ||
| ) |
Compute the nonzero basis functions and their derivatives until the 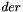 th derivative. All the functions are computed at u.
th derivative. All the functions are computed at u.
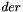 must be under or equal
must be under or equal 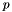 .
.The result is given as an array of size der+1 x p+1. The kth line corresponds to the kth basis functions derivatives.
The formula to compute the kth derivative at 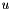 is :
is :
![\[ N_{i,p}^{(k)}(u) =p \left( \frac{N_{i,p-1}^{(k-1)}}{u_{i+p}-u_i} - \frac{N_{i+1,p-1}^{(k-1)}}{u_{i+p+1}-u_{i+1}} \right) \]](form_464.png)
where 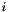 is the knot interval number in which
is the knot interval number in which 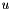 lies and
lies and 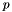 is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| u | : A real number which is between the extrimities of the knot vector |
| der | : The last derivative to be computed. |
Example : return[0] is the list of the 0th derivatives ie the basis functions. return[k] is the list of the kth derivatives.
Definition at line 364 of file vpBSpline.cpp.
References computeDersBasisFuns(), and findSpan().
|
static |
Find the knot interval in which the parameter 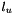 lies. Indeed
lies. Indeed 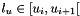
Example : The knot vector is the following 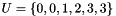 with
with 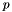 is equal to 1.
is equal to 1.
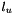 equal to 0.5 the method will retun 1.
equal to 0.5 the method will retun 1.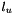 equal to 2.5 the method will retun 3.
equal to 2.5 the method will retun 3.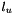 equal to 3 the method will retun 3.
equal to 3 the method will retun 3.| l_u | : The knot whose knot interval is seeked. |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
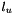 lies.
lies. Definition at line 84 of file vpBSpline.cpp.
References vpMath::maximum(), and vpMath::round().
Referenced by computeBasisFuns(), vpNurbs::computeCurveDersPoint(), computeDersBasisFuns(), vpNurbs::curveKnotIns(), findSpan(), vpNurbs::globalCurveApprox(), vpNurbs::globalCurveInterp(), and vpNurbs::refineKnotVectCurve().
| unsigned int vpBSpline::findSpan | ( | double | u | ) |
Find the knot interval in which the parameter 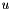 lies. Indeed
lies. Indeed 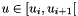
Example : The knot vector is the following 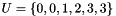 with
with 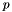 is equal to 1.
is equal to 1.
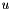 equal to 0.5 the method will retun 1.
equal to 0.5 the method will retun 1.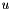 equal to 2.5 the method will retun 3.
equal to 2.5 the method will retun 3.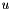 equal to 3 the method will retun 3.
equal to 3 the method will retun 3.| u | : The knot whose knot interval is seeked. |
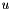 lies.
lies. Definition at line 129 of file vpBSpline.cpp.
References findSpan().
|
inline |
Gets all the control points.
| list | : A std::list containing the coordinates of the control points. |
Definition at line 140 of file vpBSpline.h.
|
inline |
Gets all the crossing points (used in the interpolation method)
| list | : A std::list containing the coordinates of the crossing points. |
Definition at line 165 of file vpBSpline.h.
|
inline |
Gets all the knots.
| list | : A std::list containing the value of the knots. |
Definition at line 152 of file vpBSpline.h.
|
inline |
Gets the degree of the B-Spline.
Definition at line 132 of file vpBSpline.h.
|
inline |
Sets all the control points.
| list | : A std::list containing the coordinates of the control points |
Definition at line 184 of file vpBSpline.h.
|
inline |
Sets all the crossing points (used in the interpolation method)
| list | : A std::list containing the coordinates of the crossing points |
Definition at line 211 of file vpBSpline.h.
|
inline |
Sets all the knots.
| list | : A std::list containing the value of the knots. |
Definition at line 197 of file vpBSpline.h.
|
inline |
Sets the degree of the B-Spline.
| degree | : the degree of the B-Spline. |
Definition at line 177 of file vpBSpline.h.