 |
Visual Servoing Platform
version 3.4.0
|
 |
Visual Servoing Platform
version 3.4.0
|
This tutorial gives some hints to boost your visual servo control law in order to speed up the time to convergence.
Note that all the material (source code and image) described in this tutorial is part of ViSP source code and could be downloaded using the following command:
To illustrate this tutorial let us consider the example tutorial-ibvs-4pts-plotter.cpp introduced in Tutorial: Image-based visual servo. This example consider an image based visual servoing using four points as visual features.
In the general case, considering 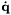 as the input velocities to the robot controller, the control laws provided in vpServo class lead to the following control law
as the input velocities to the robot controller, the control laws provided in vpServo class lead to the following control law 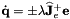 where the sign is negative for an eye in hand servo and positive for an eye to hand servo,
where the sign is negative for an eye in hand servo and positive for an eye to hand servo, 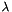 is a constant gain,
is a constant gain, 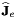 is the task Jacobian and
is the task Jacobian and 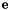 is the error to regulate to zero. As described in [2], this control law ensure an exponential decoupled decrease of the error
is the error to regulate to zero. As described in [2], this control law ensure an exponential decoupled decrease of the error 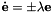 .
.
This behavior is illustrated with the next figure, where we see the exponential decrease of the eight visual features (x and y for each point) and the corresponding six velocities that are applied to the robot controller. As a consequence, velocities are high when the error is important, and very low when the error is small near the convergence. At the beginning, we can also notice velocity discontinuities with velocities varying from zero to high values in one iteration.
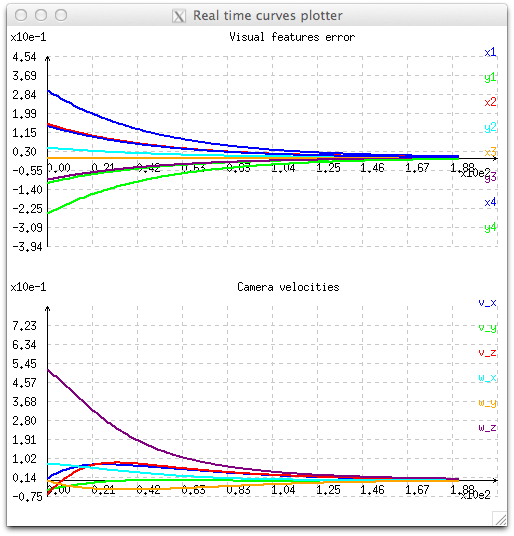
This behavior can be reproduced running tutorial-ibvs-4pts-plotter.cpp example. Here after we recall the important lines of code used to compute the control law:
As implemented in tutorial-ibvs-4pts-plotter-gain-adaptive.cpp it is possible to adapt the gain 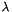 in order to depend on the infinity norm of the task Jacobian. The usage of an adaptive gain rather than a constant gain allows to reduce the convergence time. In that case the gain becomes:
in order to depend on the infinity norm of the task Jacobian. The usage of an adaptive gain rather than a constant gain allows to reduce the convergence time. In that case the gain becomes:
![\[ \lambda (x) = (\lambda_0 - \lambda_\infty) e^{ -\frac{ \lambda'_0}{\lambda_0 - \lambda_\infty}x} + \lambda_\infty \]](form_1312.png)
where:
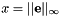 is the infinity norm of the task Jacobian to consider.
is the infinity norm of the task Jacobian to consider.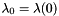 is the gain in 0, that is for very small values of
is the gain in 0, that is for very small values of 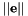
 is the gain to infinity, that is for very high values of
is the gain to infinity, that is for very high values of 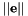
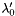 is the slope of
is the slope of 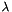 at
at 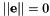
The impact of the adaptive gain is illustrated in the next figure. During the servo, velocities applied to the controller are higher, especially when the visual error 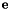 is small. But as in the previous section, using an adaptive gain doesn't insure continuous velocities especially at the first iteration.
is small. But as in the previous section, using an adaptive gain doesn't insure continuous velocities especially at the first iteration.
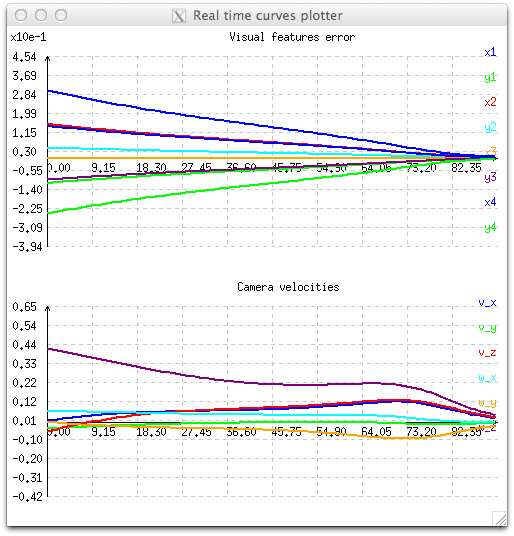
This behavior can be reproduced running tutorial-ibvs-4pts-plotter-gain-adaptive.cpp example. Compared to the previous code given in Introduction and available in tutorial-ibvs-4pts-plotter.cpp, here after we give the new lines of code that were introduced to use an adaptive gain:
To adjust the adaptative gain to your current servoing task, you need to proceed step-by-step :
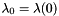 , which corresponds to the gain when the error is close to zero, place the robot close to the final desired position of the servoing task. Then, gradually increase lambda (start with lambda = 1.0) until you observe robot oscillations. A good value for
, which corresponds to the gain when the error is close to zero, place the robot close to the final desired position of the servoing task. Then, gradually increase lambda (start with lambda = 1.0) until you observe robot oscillations. A good value for  should be slightly inferior to the lambda for which oscillations start to occur.
should be slightly inferior to the lambda for which oscillations start to occur.  , which corresponds to the gain when the error is very high, move the robot further away from the target in order to get a large visual servoing error. Set lambda to a small value, like 0.1, and increase it gradually until vision is no longer able to track your features, or when the robot becomes dangerous with a velocity too high.
, which corresponds to the gain when the error is very high, move the robot further away from the target in order to get a large visual servoing error. Set lambda to a small value, like 0.1, and increase it gradually until vision is no longer able to track your features, or when the robot becomes dangerous with a velocity too high.  , is the slope of the curve
, is the slope of the curve 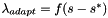 where
where 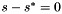 . You can keep it at 30.
. You can keep it at 30.As implemented in tutorial-ibvs-4pts-plotter-continuous-gain-adaptive.cpp it is also possible to ensure continuous sequencing to avoid velocity discontinuities. This behavior is achieved by introducing an additional term to the general form of the control law. This additional term comes from the task sequencing approach described in [27] equation (17). It allows to compute continuous velocities by avoiding abrupt changes in the command.
The form of the control law considered here is the following:
![\[ {\bf \dot q} = \pm \lambda {{\bf \widehat J}_e}^+ {\bf e} \mp \lambda {{\bf \widehat J}_{e(0)}}^+ {{\bf e}(0)} \exp(-\mu t) \]](form_1329.png)
where :
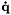 is the resulting continuous velocity command to apply to the robot controller.
is the resulting continuous velocity command to apply to the robot controller.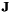 is the Jacobian of the task.
is the Jacobian of the task.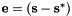 is the error to regulate.
is the error to regulate.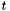 is the time.
is the time.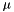 is a gain. We recommend to set this value to 4.
is a gain. We recommend to set this value to 4.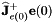 is the value of
is the value of 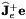 when
when 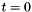 .
.The effect of continuous sequencing is illustrated in the next figure where during the first iterations velocities are starting from zero.
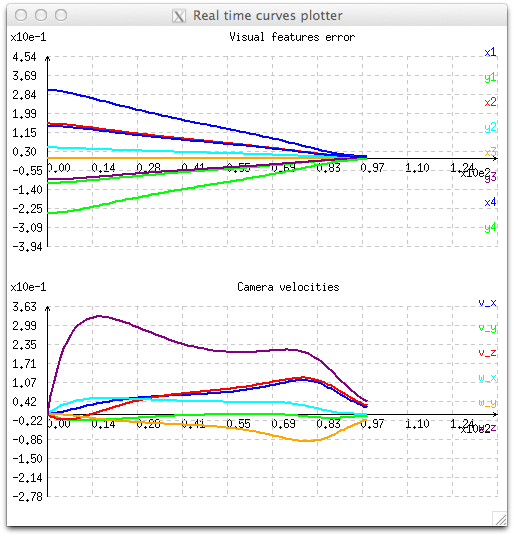
This behavior can be reproduced running tutorial-ibvs-4pts-plotter-continuous-gain-adaptive.cpp example. Compared to the previous code given in Using an adaptive gain and available in tutorial-ibvs-4pts-plotter-gain-adaptive.cpp, here after we give the new line of code that were introduced to ensure continuous sequencing:
You are now ready to see the Tutorial: PBVS with Panda 7-dof robot from Franka Emika that will show how to use adaptive gain and task sequencing on a real robot.