 |
Visual Servoing Platform
version 3.3.0 under development (2020-02-17)
|
 |
Visual Servoing Platform
version 3.3.0 under development (2020-02-17)
|
#include <visp3/core/vpExponentialMap.h>
Static Public Member Functions | |
| static vpHomogeneousMatrix | direct (const vpColVector &v) |
| static vpHomogeneousMatrix | direct (const vpColVector &v, const double &delta_t) |
| static vpColVector | inverse (const vpHomogeneousMatrix &M) |
| static vpColVector | inverse (const vpHomogeneousMatrix &M, const double &delta_t) |
Direct or inverse exponential map computation.
The exponential map gives the relationship between the velocity of a moving body and its displacement:
![\[ \exp({^c}{\bf v}_c) = {^{c(t)}}{\bf M}_{c(t+\Delta t)} \]](form_62.png)
where 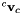 is the velocity skew vector applied during
is the velocity skew vector applied during 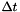 seconds at point
seconds at point 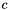 in frame
in frame 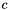 , while
, while 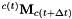 is the corresponding displacement.
is the corresponding displacement.
This class allows to compute the direct or the inverse exponential map.
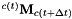 using
using 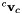 as input:
as input:
![\[ {^{o}}{\bf M}_{c(t+\Delta t)} = {^{o}}{\bf M}_{c(t)} \exp({^c}{\bf v}_c) \]](form_69.png)
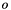 is a reference frame. With direct(), the velocity skew vector
is a reference frame. With direct(), the velocity skew vector 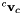 is applied during 1 second considering
is applied during 1 second considering 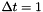 . With direct(const vpColVector &, const double &) the sampling time can be set to an other value where the second argument is
. With direct(const vpColVector &, const double &) the sampling time can be set to an other value where the second argument is 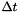 .
.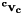 from the displacement
from the displacement 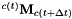 measured during a time interval
measured during a time interval 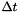 . With inverse() the time interval also called sampling time is set to 1 second. With inverse(const vpHomogeneousMatrix &, const double &) the sampling time can be set to an other value where the second argument is
. With inverse() the time interval also called sampling time is set to 1 second. With inverse(const vpHomogeneousMatrix &, const double &) the sampling time can be set to an other value where the second argument is 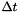 .
.A displacement 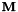 is represented as an homogeneous matrix implemented in vpHomogeneousMatrix. A velocities
is represented as an homogeneous matrix implemented in vpHomogeneousMatrix. A velocities 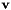 is represented as a 6 dimension velocity skew vector
is represented as a 6 dimension velocity skew vector ![$ [v, \omega] $](form_78.png) , where
, where 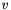 is a velocity translation vector with values in m/s and
is a velocity translation vector with values in m/s and 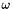 a velocity rotation vector with values expressed in rad/s.
a velocity rotation vector with values expressed in rad/s.
Definition at line 93 of file vpExponentialMap.h.
|
static |
Compute the exponential map. The inverse function is inverse(). The sampling time is here set to 1 second. To use an other value you should use direct(const vpColVector &, const double &).
| v | : Instantaneous velocity skew represented by a 6 dimension vector ![$ {\bf v} = [v, \omega] $](form_516.png) where where 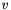 is a translation velocity vector and is a translation velocity vector and 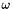 is a rotation velocity vector. is a rotation velocity vector. |
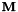 computed from an instantaneous velocity
computed from an instantaneous velocity 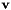 , where
, where 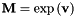 is the displacement of the object when the velocity
is the displacement of the object when the velocity 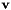 is applied during 1 second.
is applied during 1 second.Definition at line 59 of file vpExponentialMap.cpp.
Referenced by vpPoseFeatures::computePose(), vpMbDepthDenseTracker::computeVVS(), vpMbDepthNormalTracker::computeVVS(), vpMbEdgeKltTracker::computeVVS(), vpMbKltMultiTracker::computeVVS(), vpMbEdgeKltMultiTracker::computeVVS(), vpMbEdgeMultiTracker::computeVVS(), vpMbGenericTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpMbEdgeMultiTracker::computeVVSFirstPhasePoseEstimation(), vpMbEdgeTracker::computeVVSFirstPhasePoseEstimation(), vpPose::poseVirtualVS(), vpPose::poseVirtualVSrobust(), vpRobotBebop2::setVelocity(), vpSimulatorCamera::setVelocity(), vpRobotCamera::setVelocity(), and vpMbGenericTracker::track().
|
static |
Compute the exponential map. The inverse function is inverse().
| v | : Instantaneous velocity skew represented by a 6 dimension vector ![$ {\bf v} = [v, \omega] $](form_516.png) where where 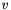 is a translation velocity vector and is a translation velocity vector and 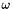 is a rotation velocity vector. is a rotation velocity vector. |
| delta_t | : Sampling time 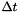 . Time during which the velocity . Time during which the velocity 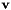 is applied. is applied. |
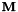 computed from an instantaneous velocity
computed from an instantaneous velocity 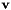 , where
, where 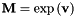 is the displacement of the object when the velocity
is the displacement of the object when the velocity 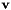 is applied during
is applied during 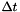 seconds.
seconds.Definition at line 79 of file vpExponentialMap.cpp.
References vpRotationMatrix::buildFrom(), vpException::dimensionError, vpHomogeneousMatrix::insert(), vpMath::mcosc(), vpMath::msinc(), vpMath::sinc(), and vpArray2D< Type >::size().
|
static |
Computes an instantaneous velocity skew from an homogeneous matrix. The inverse function is the exponential map, see direct().
| M | : An homogeneous matrix corresponding to the displacement of an object during 1 second. |
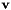 represented by a 6 dimension vector
represented by a 6 dimension vector ![$ [v, \omega] $](form_78.png) where
where 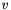 is a translation velocity vector and
is a translation velocity vector and 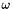 is a rotation velocity vector.
is a rotation velocity vector.Definition at line 202 of file vpExponentialMap.cpp.
Referenced by vpRobotBiclops::getDisplacement(), vpRobotAfma4::getVelocity(), vpRobotAfma6::getVelocity(), vpRobotViper650::getVelocity(), and vpRobotViper850::getVelocity().
|
static |
Compute an instantaneous velocity from an homogeneous matrix. The inverse function is the exponential map, see direct().
| M | : An homogeneous matrix corresponding to the displacement of an object during 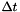 seconds. seconds. |
| delta_t | : Sampling time 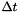 . Time during which the displacement is applied. . Time during which the displacement is applied. |
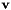 represented by a 6 dimension vector
represented by a 6 dimension vector ![$ [v, \omega] $](form_78.png) where
where 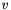 is a translation velocity vector and
is a translation velocity vector and 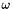 is a rotation velocity vector.
is a rotation velocity vector.Definition at line 221 of file vpExponentialMap.cpp.
References vpThetaUVector::buildFrom(), vpHomogeneousMatrix::extract(), vpMath::mcosc(), vpMath::msinc(), and vpMath::sinc().