Visual Servoing Platform  version 3.1.0
Public Types | Public Member Functions | Static Public Member Functions | List of all members
vpHinkley Class Reference
core: Core module » Mathematics » Other tools

#include <visp3/core/vpHinkley.h>

Public Types

enum  vpHinkleyJumpType { noJump, downwardJump, upwardJump }
 

Public Member Functions

 vpHinkley ()
 
 ~vpHinkley ()
 
 vpHinkley (double alpha, double delta)
 
void init ()
 
void init (double alpha, double delta)
 
void setDelta (double delta)
 
void setAlpha (double alpha)
 
vpHinkleyJumpType testDownwardJump (double signal)
 
vpHinkleyJumpType testUpwardJump (double signal)
 
vpHinkleyJumpType testDownUpwardJump (double signal)
 
double getMean ()
 
double getSk ()
 
double getMk ()
 
double getTk ()
 
double getNk ()
 

Static Public Member Functions

static void print (vpHinkleyJumpType jump)
 

Detailed Description

This class implements the Hinkley's cumulative sum test.

Author
Fabien Spindler (Fabie.nosp@m.n.Sp.nosp@m.indle.nosp@m.r@ir.nosp@m.isa.f.nosp@m.r), Irisa / Inria Rennes

The Hinkley's cumulative sum test is designed to detect jump in mean of an observed signal 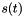$ s(t) $. It is known to be robust (by taking into account all the past of the observed quantity), efficient, and inducing a very low computational load. The other attractive features of this test are two-fold. First, it can straightforwardly and accurately provide the jump instant. Secondly, due to its formulation (cumulative sum test), it can simultaneously handle both very abrupt and important changes, and gradual smaller ones without adapting the involved thresholds.

Two tests are performed in parallel to look for downwards or upwards jumps in 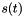$ s(t) $, respectively defined by:

\[ S_k = \sum_{t=0}^{k} (s(t) - m_0 + \frac{\delta}{2}) \]

\[ M_k = \max_{0 \leq i \leq k} S_i\]

\[ T_k = \sum_{t=0}^{k} (s(t) - m_0 - \frac{\delta}{2}) \]

\[ N_k = \max_{0 \leq i \leq k} T_i\]

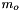In which $m_o$ is computed on-line and corresponds to the mean of the signal 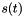$ s(t) $ we want to detect a jump. 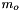$m_o$ is re-initialized at zero after each jump detection. 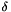$\delta$ denotes the jump minimal magnitude that we want to detect and 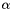$\alpha$ is a predefined threshold. These values are set by default to 0.2 in the default constructor vpHinkley(). To modify the default values use setAlpha() and setDelta() or the vpHinkley(double alpha, double delta) constructor.

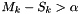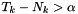A downward jump is detected if $ M_k - S_k > \alpha $. A upward jump is detected if $ T_k - N_k > \alpha $.

To detect only downward jumps in 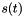$ s(t) $ use testDownwardJump().To detect only upward jumps in 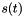$ s(t) $ use testUpwardJump(). To detect both, downard and upward jumps use testDownUpwardJump().

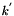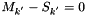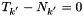If a jump is detected, the jump location is given by the last instant $k^{'}$ when $ M_{k^{'}} - S_{k^{'}} = 0 $, or $ T_{k^{'}} - N_{k^{'}} = 0 $.

Definition at line 96 of file vpHinkley.h.

Member Enumeration Documentation

◆ vpHinkleyJumpType

enum vpHinkley::vpHinkleyJumpType

Indicates if a jump is detected by the Hinkley test.

Enumerator
noJump 

No jump is detected by the Hinkley test.

downwardJump 

A downward jump is detected by the Hinkley test.

upwardJump 

An upward jump is detected by the Hinkley test.

Definition at line 102 of file vpHinkley.h.

Constructor & Destructor Documentation

◆ vpHinkley() [1/2]

vpHinkley::vpHinkley ( )

Constructor.

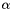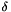Call init() to initialise the Hinkley's test and set $\alpha$ and $\delta$ to default values.

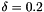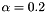By default $ \delta = 0.2 $ and $ \alpha = 0.2$. Use setDelta() and setAlpha() to modify these values.

Definition at line 76 of file vpHinkley.cpp.

◆ ~vpHinkley()

vpHinkley::~vpHinkley ( )

Destructor.

Definition at line 125 of file vpHinkley.cpp.

◆ vpHinkley() [2/2]

vpHinkley::vpHinkley ( double  alpha_val,
double  delta_val 
)

Constructor.

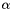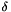Call init() to initialise the Hinkley's test and set $\alpha$ and $\delta$ thresholds.

Parameters
alpha_val: 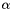$\alpha$ is a predefined threshold.
delta_val: 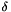$\delta$ denotes the jump minimal magnitude that we want to detect.
See also
setAlpha(), setDelta()

Definition at line 94 of file vpHinkley.cpp.

Member Function Documentation

◆ getMean()

double vpHinkley::getMean ( )
inline
Returns
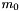The mean value $m_0$ of the signal $ s(t) $.

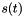Definition at line 128 of file vpHinkley.h.

◆ getMk()

double vpHinkley::getMk ( )
inline
Returns
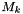The value of $M_k$, the maximum value of $S_k$.

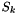Definition at line 139 of file vpHinkley.h.

◆ getNk()

double vpHinkley::getNk ( )
inline
Returns
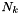The value of $N_k$, the maximum value of $T_k$.

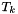Definition at line 151 of file vpHinkley.h.

◆ getSk()

double vpHinkley::getSk ( )
inline
Returns
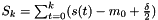
The value of $S_k = \sum_{t=0}^{k} (s(t) - m_0 + \frac{\delta}{2})$

Definition at line 134 of file vpHinkley.h.

◆ getTk()

double vpHinkley::getTk ( )
inline
Returns
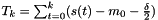
The value of $T_k = \sum_{t=0}^{k} (s(t) - m_0 - \frac{\delta}{2})$

Definition at line 146 of file vpHinkley.h.

◆ init() [1/2]

void vpHinkley::init ( )

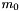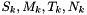Initialise the Hinkley's test by setting the mean signal value $m_0$ to zero as well as $S_k, M_k, T_k, N_k$.

Definition at line 133 of file vpHinkley.cpp.

◆ init() [2/2]

void vpHinkley::init ( double  alpha_val,
double  delta_val 
)

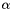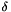Call init() to initialise the Hinkley's test and set $\alpha$ and $\delta$ thresholds.

Parameters
alpha_val: 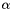$\alpha$ is a predefined threshold.
delta_val: 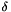$\delta$ denotes the jump minimal magnitude that we want to detect.
See also
setAlpha(), setDelta()

Definition at line 112 of file vpHinkley.cpp.

References init(), setAlpha(), and setDelta().

Referenced by init().

◆ print()

void vpHinkley::print ( vpHinkley::vpHinkleyJumpType  jump)
static

Definition at line 422 of file vpHinkley.cpp.

References downwardJump, noJump, and upwardJump.

◆ setAlpha()

void vpHinkley::setAlpha ( double  alpha_val)

Set the value of 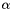$\alpha$, a predefined threshold.

See also
setDelta()

Definition at line 162 of file vpHinkley.cpp.

Referenced by init().

◆ setDelta()

void vpHinkley::setDelta ( double  delta)

Set the value of 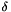$\delta$, the jump minimal magnetude that we want to detect.

See also
setAlpha()

Definition at line 153 of file vpHinkley.cpp.

Referenced by init().

◆ testDownUpwardJump()

vpHinkley::vpHinkleyJumpType vpHinkley::testDownUpwardJump ( double  signal)

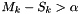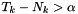Perform the Hinkley test. A downward jump is detected if $ M_k - S_k > \alpha $. An upward jump is detected if $ T_k - N_k > \alpha $.

Parameters
signal: Observed signal 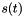$ s(t) $.
See also
setDelta(), setAlpha(), testDownwardJump(), testUpwardJump()

Definition at line 293 of file vpHinkley.cpp.

References downwardJump, vpMath::maximum(), noJump, upwardJump, and vpCDEBUG.

◆ testDownwardJump()

vpHinkley::vpHinkleyJumpType vpHinkley::testDownwardJump ( double  signal)

Perform the Hinkley test. A downward jump is detected if 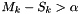$ M_k - S_k > \alpha $.

Parameters
signal: Observed signal 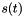$ s(t) $.
See also
setDelta(), setAlpha(), testUpwardJump()

Definition at line 174 of file vpHinkley.cpp.

References downwardJump, noJump, upwardJump, and vpCDEBUG.

◆ testUpwardJump()

vpHinkley::vpHinkleyJumpType vpHinkley::testUpwardJump ( double  signal)

Perform the Hinkley test. An upward jump is detected if 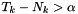$ T_k - N_k > \alpha $.

Parameters
signal: Observed signal 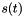$ s(t) $.
See also
setDelta(), setAlpha(), testDownwardJump()

Definition at line 234 of file vpHinkley.cpp.

References downwardJump, noJump, upwardJump, and vpCDEBUG.