 |
ViSP
2.9.0
|
 |
ViSP
2.9.0
|
#include <vpHomography.h>
Static Public Member Functions | |
| static void | DLT (const std::vector< double > &xb, const std::vector< double > &yb, const std::vector< double > &xa, const std::vector< double > &ya, vpHomography &aHb, bool normalization=true) |
| static void | HLM (const std::vector< double > &xb, const std::vector< double > &yb, const std::vector< double > &xa, const std::vector< double > &ya, bool isplanar, vpHomography &aHb) |
| static bool | ransac (const std::vector< double > &xb, const std::vector< double > &yb, const std::vector< double > &xa, const std::vector< double > &ya, vpHomography &aHb, std::vector< bool > &inliers, double &residual, unsigned int nbInliersConsensus, double threshold, bool normalization=true) |
| static vpImagePoint | project (const vpCameraParameters &cam, const vpHomography &bHa, const vpImagePoint &iPa) |
| static vpPoint | project (const vpHomography &bHa, const vpPoint &Pa) |
| static void | robust (const std::vector< double > &xb, const std::vector< double > &yb, const std::vector< double > &xa, const std::vector< double > &ya, vpHomography &aHb, std::vector< bool > &inlier, double &residual, double weights_threshold=0.4, unsigned int niter=4, bool normalization=true) |
Public Attributes | |
| double * | data |
Friends | |
| VISP_EXPORT std::ostream & | operator<< (std::ostream &s, const vpHomography &H) |
Deprecated functions | |
| vp_deprecated void | print () |
| static vp_deprecated void | computeDisplacement (const vpMatrix H, const double x, const double y, vpList< vpRotationMatrix > &vR, vpList< vpTranslationVector > &vT, vpList< vpColVector > &vN) |
| static void | DLT (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb) |
| static vp_deprecated void | HartleyDLT (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb) |
| static void | HLM (unsigned int n, double *xb, double *yb, double *xa, double *ya, bool isplan, vpHomography &aHb) |
| static vp_deprecated bool | ransac (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb, int consensus=1000, double threshold=1e-6) |
| static vp_deprecated bool | ransac (unsigned int n, double *xb, double *yb, double *xa, double *ya, vpHomography &aHb, vpColVector &inliers, double residual=0.1, int consensus=1000, double threshold=1e-6, double areaThreshold=0.0) |
This class aims to compute the homography wrt.two images.
These two images are both described by a set of points. The 2 sets (one per image) are sets of corresponding points : for a point in a image, there is the corresponding point (image of the same 3D point) in the other image points set. These 2 sets are the only data needed to compute the homography. One method used is the one introduced by Ezio Malis during his PhD [17]. A normalization is carried out on this points in order to improve the conditioning of the problem, what leads to improve the stability of the result.
Store and compute the homography such that
![\[ ^a{\bf p} = ^a{\bf H}_b\; ^b{\bf p} \]](form_54.png)
with
![\[ ^a{\bf H}_b = ^a{\bf R}_b + \frac{^a{\bf t}_b}{^bd} { ^b{\bf n}^T} \]](form_38.png)
The Tutorial: Homography estimation from points explains how to use this class.
The example below shows also how to manipulate this class to first compute a ground truth homography from camera poses, project pixel coordinates points using an homography and lastly estimate an homography from a subset of 4 matched points in frame a and frame b respectively.
Definition at line 178 of file vpHomography.h.
| vpHomography::vpHomography | ( | ) |
initialize an homography as Identity
Definition at line 64 of file vpHomography.cpp.
References data, and setIdentity().
| vpHomography::vpHomography | ( | const vpHomography & | H | ) |
initialize an homography from another homography
Definition at line 75 of file vpHomography.cpp.
References data.
| vpHomography::vpHomography | ( | const vpHomogeneousMatrix & | aMb, |
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
initialize an homography from another homography
Definition at line 85 of file vpHomography.cpp.
References buildFrom(), and data.
| vpHomography::vpHomography | ( | const vpRotationMatrix & | aRb, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 99 of file vpHomography.cpp.
References buildFrom(), and data.
| vpHomography::vpHomography | ( | const vpThetaUVector & | tu, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 91 of file vpHomography.cpp.
References buildFrom(), and data.
| vpHomography::vpHomography | ( | const vpPoseVector & | arb, |
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 107 of file vpHomography.cpp.
References buildFrom(), and data.
|
virtual |
Definition at line 113 of file vpHomography.cpp.
References data.
| void vpHomography::buildFrom | ( | const vpRotationMatrix & | aRb, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 141 of file vpHomography.cpp.
Referenced by vpHomography().
| void vpHomography::buildFrom | ( | const vpThetaUVector & | tu, |
| const vpTranslationVector & | atb, | ||
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 130 of file vpHomography.cpp.
| void vpHomography::buildFrom | ( | const vpPoseVector & | arb, |
| const vpPlane & | bP | ||
| ) |
Construction from Translation and rotation and a plane.
Definition at line 152 of file vpHomography.cpp.
References vpHomogeneousMatrix::buildFrom().
| void vpHomography::buildFrom | ( | const vpHomogeneousMatrix & | aMb, |
| const vpPlane & | bP | ||
| ) |
Construction from homogeneous matrix and a plane.
Definition at line 121 of file vpHomography.cpp.
| void vpHomography::computeDisplacement | ( | vpRotationMatrix & | aRb, |
| vpTranslationVector & | atb, | ||
| vpColVector & | n | ||
| ) |
Compute the camera displacement between two images from the homography 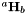 which is here an implicit parameter (*this).
which is here an implicit parameter (*this).
| aRb | : Rotation matrix as an output 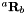 . . |
| atb | : Translation vector as an output 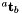 . . |
| n | : Normal vector to the plane as an output. |
Definition at line 64 of file vpHomographyExtract.cpp.
Referenced by computeDisplacement().
| void vpHomography::computeDisplacement | ( | const vpColVector & | nd, |
| vpRotationMatrix & | aRb, | ||
| vpTranslationVector & | atb, | ||
| vpColVector & | n | ||
| ) |
Compute the camera displacement between two images from the homography 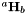 which is here an implicit parameter (*this).
which is here an implicit parameter (*this).
Camera displacement between 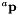 and
and 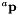 is represented as a rotation matrix
is represented as a rotation matrix 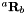 and a translation vector
and a translation vector 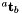 from which an homogenous matrix can be build (vpHomogeneousMatrix).
from which an homogenous matrix can be build (vpHomogeneousMatrix).
| nd | : Input normal vector to the plane used to compar with the normal vector n extracted from the homography. |
| aRb | : Rotation matrix as an output 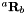 . . |
| atb | : Translation vector as an output 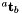 . . |
| n | : Normal vector to the plane as an output. |
Definition at line 97 of file vpHomographyExtract.cpp.
References computeDisplacement().
|
static |
Definition at line 1342 of file vpHomographyExtract.cpp.
References vpList< type >::addRight(), vpList< type >::kill(), vpRotationMatrix::setIdentity(), vpMath::sqr(), vpMatrix::svd(), and vpRotationMatrix::t().
|
static |
From couples of matched points 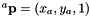 in image a and
in image a and 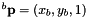 in image b with homogeneous coordinates, computes the homography matrix by resolving
in image b with homogeneous coordinates, computes the homography matrix by resolving 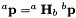 using the DLT (Direct Linear Transform) algorithm.
using the DLT (Direct Linear Transform) algorithm.
At least 4 couples of points are needed.
To do so, we use the DLT algorithm on the data, ie we resolve the linear system by SDV : 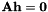 where
where 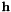 is the vector with the terms of
is the vector with the terms of 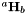 and
and 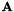 depends on the points coordinates.
depends on the points coordinates.
For each point, in homogeneous coordinates we have:
![\[ ^a{\bf p} = ^a{\bf H}_b\; ^b{\bf p} \]](form_54.png)
which is equivalent to:
![\[ ^a{\bf p} \times {^a{\bf H}_b \; ^b{\bf p}} =0 \]](form_71.png)
If we note 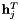 the
the 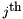 line of
line of 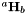 , we can write:
, we can write:
![\[ ^a{\bf H}_b \; ^b{\bf p} = \left( \begin{array}{c}\mathbf{h}_1^T \;^b{\bf p} \\\mathbf{h}_2^T \; ^b{\bf p} \\\mathbf{h}_3^T \;^b{\bf p} \end{array}\right) \]](form_72.png)
Setting 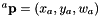 , the cross product can be rewritten by:
, the cross product can be rewritten by:
![\[ ^a{\bf p} \times ^a{\bf H}_b \; ^b{\bf p} =\left( \begin{array}{c}y_{a}\mathbf{h}_3^T \; ^b{\bf p}-w_{a}\mathbf{h}_2^T \; ^b{\bf p} \\w_{a}\mathbf{h}_1^T \; ^b{\bf p} -x_{a}\mathbf{h}_3^T \; ^b{\bf p} \\x_{a}\mathbf{h}_2^T \; ^b{\bf p}- y_{a}\mathbf{h}_1^T \; ^b{\bf p}\end{array}\right) \]](form_74.png)
![\[ \underbrace{\left( \begin{array}{ccc}\mathbf{0}^T & -w_{a} \; ^b{\bf p}^T & y_{a} \; ^b{\bf p}^T \\ w_{a} \; ^b{\bf p}^T&\mathbf{0}^T & -x_{a} \; ^b{\bf p}^T \\ -y_{a} \; ^b{\bf p}^T & x_{a} \; ^b{\bf p}^T & \mathbf{0}^T\end{array}\right)}_{\mathbf{A}_i (3\times 9)} \underbrace{\left( \begin{array}{c}\mathbf{h}_{1}^{T} \\ \mathbf{h}_{2}^{T}\\\mathbf{h}_{3}^{T}\end{array}\right)}_{\mathbf{h} (9\times 1)}=0 \]](form_75.png)
leading to an homogeneous system to be solved: 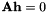 with
with 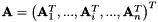 .
.
It can be solved using an SVD decomposition:
![\[\bf A = UDV^T \]](form_69.png)
h is the column of V associated with the smalest singular value of A
| xb,yb | : Coordinates vector of matched points in image b. These coordinates are expressed in meters. |
| xa,ya | : Coordinates vector of matched points in image a. These coordinates are expressed in meters. |
| aHb | : Estimated homography that relies the transformation from image a to image b. |
| normalization | : When set to true, the coordinates of the points are normalized. The normalization carried out is the one preconized by Hartley. |
| vpMatrixException::rankDeficient | : When the rank of the matrix that should be 8 is deficient. |
Definition at line 503 of file vpHomographyDLT.cpp.
References vpMatrix::column(), vpException::dimensionError, vpException::fatalError, vpMatrixException::rankDeficient, vpMatrix::resize(), vpMatrix::svd(), vpERROR_TRACE, and vpTRACE.
Referenced by HartleyDLT(), and ransac().
|
static |
Computes the homography matrix wrt. the data using the DLT (Direct Linear Transform) algorithm.
Computes H such as
![\[ ^a{\bf p} = ^a{\bf H}_b\; ^b{\bf p} \]](form_54.png)
To do so, we use the DLT algorithm on the data, ie we resolve the linear system by SDV : 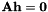 .
. 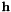 is the vector with the terms of
is the vector with the terms of 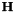 ,
,
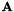 depends on the points coordinates.
depends on the points coordinates.
At least 4 correspondant points couples are needed.
For each point, in homogeneous coordinates we have:
![\[ \mathbf{p}_{a}= \mathbf{H}\mathbf{p}_{b} \]](form_59.png)
which is equivalent to:
![\[ \mathbf{p}_{a} \times \mathbf{H}\mathbf{p}_{b} =0 \]](form_60.png)
If we note 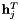 the
the 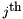 line of
line of 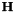 , we can write:
, we can write:
![\[ \mathbf{H}\mathbf{p}_{b} = \left( \begin{array}{c}\mathbf{h}_1^T\mathbf{p}_{b} \\\mathbf{h}_2^T\mathbf{p}_{b} \\\mathbf{h}_3^T \mathbf{p}_{b} \end{array}\right) \]](form_63.png)
Setting 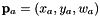 , the cross product can be rewritten by:
, the cross product can be rewritten by:
![\[ \mathbf{p}_{a} \times \mathbf{H}\mathbf{p}_{b} =\left( \begin{array}{c}y_{a}\mathbf{h}_3^T\mathbf{p}_{b}-w_{a}\mathbf{h}_2^T\mathbf{p}_{b} \\w_{a}\mathbf{h}_1^T\mathbf{p}_{b} -x_{a}\mathbf{h}_3^T \mathbf{p}_{b} \\x_{a}\mathbf{h}_2^T \mathbf{p}_{b}- y_{a}\mathbf{h}_1^T\mathbf{p}_{b}\end{array}\right) \]](form_65.png)
![\[ \underbrace{\left( \begin{array}{ccc}\mathbf{0}^T & -w_{a} \mathbf{p}_{b}^T & y_{a} \mathbf{p}_{b}^T \\ w_{a} \mathbf{p}_{b}^T&\mathbf{0}^T & -x_{a} \mathbf{p}_{b}^T \\ -y_{a} \mathbf{p}_{b}^T & x_{a} \mathbf{p}_{b}^T & \mathbf{0}^T\end{array}\right)}_{\mathbf{A}_i (3\times 9)} \underbrace{\left( \begin{array}{c}\mathbf{h}_{1}^{T} \\ \mathbf{h}_{2}^{T}\\\mathbf{h}_{3}^{T}\end{array}\right)}_{\mathbf{h} (9\times 1)}=0 \]](form_66.png)
leading to an homogeneous system to be solve: 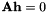 with
with 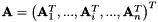 .
.
It can be solved using an SVD decomposition:
![\[\bf A = UDV^T \]](form_69.png)
h is the column of V associated with the smalest singular value of A
| vpMatrixException::rankDeficient | : When the rank of the matrix that should be 8 is deficient. |
Definition at line 338 of file vpHomographyDLT.cpp.
References vpMatrix::column(), vpMatrixException::rankDeficient, vpMatrix::resize(), vpMatrix::svd(), vpERROR_TRACE, and vpTRACE.
|
inline |
Return the number of columns of the homography matrix.
Definition at line 259 of file vpHomography.h.
|
inline |
Return the number of rows of the homography matrix.
Definition at line 257 of file vpHomography.h.
|
static |
Computes the homography matrix using the DLT (Direct Linear Transform) algorithm on normalized data.
Normalizes data, computes H wrt. these normalized data and denormalizes the result. The normalization carried out is the one preconized by Hartley . At least 4 correspondant points couples are needed.
| vpMatrixException::rankDeficient | : When the rank of the matrix that should be 8 is deficient. |
Definition at line 225 of file vpHomographyDLT.cpp.
|
static |
From couples of matched points 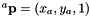 in image a and
in image a and 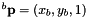 in image b with homogeneous coordinates, computes the homography matrix by resolving
in image b with homogeneous coordinates, computes the homography matrix by resolving 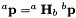 using Ezio Malis linear method (HLM) [16].
using Ezio Malis linear method (HLM) [16].
This method can consider points that are planar or non planar. The algorithm for planar scene implemented in this file is described in Ezio Malis PhD thesis [17].
| xb,yb | : Coordinates vector of matched points in image b. These coordinates are expressed in meters. |
| xa,ya | : Coordinates vector of matched points in image a. These coordinates are expressed in meters. |
| isplanar | : If true the points are assumed to be in a plane, otherwise there are assumed to be non planar. |
| aHb | : Estimated homography that relies the transformation from image a to image b. |
If the boolean isplanar is true the points are assumed to be in a plane otherwise there are assumed to be non planar.
Definition at line 828 of file vpHomographyMalis.cpp.
References vpException::dimensionError, and vpException::fatalError.
Referenced by HLM(), and vpPose::poseFromRectangle().
|
static |
Computes the homography matrix from planar [17] or non planar points using Ezio Malis linear method (HLM) [16].
Computes H such as
![\[ ^a{\bf p} = ^a{\bf H}_b\; ^b{\bf p} \]](form_54.png)
The algorithm for 2D scene implemented in this file is described in Ezio Malis PhD thesis.
If the boolean isplanar is true the point is assumed to be in a plane otherwise there are assumed to be planar.
The reference planar is the plane build from the 3 first points.
Definition at line 783 of file vpHomographyMalis.cpp.
References HLM().
| vpHomography vpHomography::inverse | ( | ) | const |
invert the homography
Invert the homography.
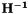
Definition at line 222 of file vpHomography.cpp.
References vpMatrix::pseudoInverse().
Referenced by vpTemplateTrackerWarpHomography::getParamInverse(), and inverse().
| void vpHomography::inverse | ( | vpHomography & | bHa | ) | const |
invert the homography
Invert the homography.
| bHa | : 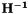 with H = *this. with H = *this. |
Definition at line 243 of file vpHomography.cpp.
References inverse().
| void vpHomography::load | ( | std::ifstream & | f | ) |
Load an homography from a file.
Read an homography in a file, verify if it is really an homogeneous matrix.
| f | : the file. |
Definition at line 420 of file vpHomography.cpp.
References vpException::ioError.
| vpHomography vpHomography::operator* | ( | const vpHomography & | H | ) | const |
Multiplication by an homography.
| H | : Homography to multiply with. |
Definition at line 275 of file vpHomography.cpp.
| vpHomography vpHomography::operator* | ( | const double & | v | ) | const |
Multiply an homography by a scalar.
| v | : Value of the scalar. |
Definition at line 325 of file vpHomography.cpp.
References data.
| vpColVector vpHomography::operator* | ( | const vpColVector & | b | ) | const |
Operation a = aHb * b.
| b | : 3 dimension vector. |
Definition at line 296 of file vpHomography.cpp.
References vpException::dimensionError, and vpColVector::size().
| vpHomography vpHomography::operator/ | ( | const double & | v | ) | const |
Divide an homography by a scalar.
| v | : Value of the scalar. |
Definition at line 349 of file vpHomography.cpp.
References data, and vpException::divideByZeroError.
| vpHomography & vpHomography::operator/= | ( | double | v | ) |
Divide all the element of the homography matrix by v : Hij = Hij / v.
Definition at line 365 of file vpHomography.cpp.
References data, and vpException::divideByZeroError.
| vpHomography & vpHomography::operator= | ( | const vpHomography & | H | ) |
Copy operator. Allow operation such as aHb = H
| H | : Homography matrix to be copied. |
Definition at line 386 of file vpHomography.cpp.
| vpHomography & vpHomography::operator= | ( | const vpMatrix & | H | ) |
Copy operator. Allow operation such as aHb = H
| H | : Matrix to be copied. |
Definition at line 401 of file vpHomography.cpp.
References vpException::dimensionError, vpMatrix::getCols(), and vpMatrix::getRows().
|
inline |
Write elements Hij (usage : H[i][j] = x )
Definition at line 270 of file vpHomography.h.
|
inline |
Read elements Hij (usage : x = H[i][j] )
Definition at line 272 of file vpHomography.h.
| void vpHomography::print | ( | ) |
Print the matrix.
Print the homography as a matrix.
Definition at line 440 of file vpHomography.cpp.
|
static |
Given iPa a point with coordinates 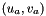 expressed in pixel in image a, and the homography
expressed in pixel in image a, and the homography bHa that links image a and b, computes the coordinates of the point 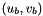 in the image b using the camera parameters matrix
in the image b using the camera parameters matrix 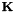 .
.
Compute 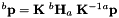 with
with 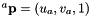 and
and 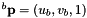
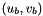 .
. Definition at line 537 of file vpHomography.cpp.
References vpCameraParameters::get_K(), vpCameraParameters::get_K_inverse(), vpImagePoint::get_u(), and vpImagePoint::get_v().
|
static |
Given Pa a point with normalized coordinates 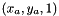 in the image plane a, and the homography
in the image plane a, and the homography bHa that links image a and b, computes the normalized coordinates of the point 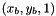 in the image plane b.
in the image plane b.
Compute 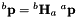 with
with 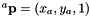 and
and 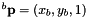
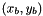 .
. Definition at line 559 of file vpHomography.cpp.
References vpPoint::get_x(), vpPoint::get_y(), vpPoint::set_x(), and vpPoint::set_y().
|
static |
From couples of matched points 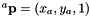 in image a and
in image a and 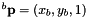 in image b with homogeneous coordinates, computes the homography matrix by resolving
in image b with homogeneous coordinates, computes the homography matrix by resolving 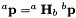 using Ransac algorithm.
using Ransac algorithm.
| xb,yb | : Coordinates vector of matched points in image b. These coordinates are expressed in meters. |
| xa,ya | : Coordinates vector of matched points in image a. These coordinates are expressed in meters. |
| aHb | : Estimated homography that relies the transformation from image a to image b. |
| inliers | : Vector that indicates if a matched point is an inlier (true) or an outlier (false). |
| residual | : Global residual computed as 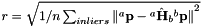 with with 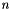 the number of inliers. the number of inliers. |
| nbInliersConsensus | : Minimal number of points requested to fit the estimated homography. |
| threshold | : Threshold for outlier removing. A point is considered as an outlier if the reprojection error 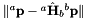 is greater than this threshold. is greater than this threshold. |
| normalization | : When set to true, the coordinates of the points are normalized. The normalization carried out is the one preconized by Hartley. |
Definition at line 435 of file vpHomographyRansac.cpp.
References vpException::dimensionError, DLT(), vpException::fatalError, and vpERROR_TRACE.
|
static |
Definition at line 319 of file vpHomographyRansac.cpp.
References data, and vpRansac< vpTransformation >::ransac().
|
static |
Computes homography matrix 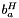 such as
such as 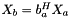 with
with 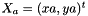 and
and 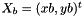 .
.
| n | : Number of points. |
| xb,yb | : Coordinates of the points in 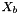 vector. vector. |
| xa,ya | : Coordinates of the points in 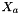 vector. vector. |
| bHa | : Homography matrix computed from 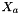 and and 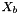 vectors. vectors. |
| inliers | : n dimention vector indicating if a point is an inlier (value 1.0) or an outlier (value 0). Matches are stocked in inliers vector column. |
| residual | : Residual. Not used. |
| consensus | : Minimal number of points (less than n) fitting the model. |
| threshold | : Threshold for outlier removing. |
| areaThreshold | : Ensure that the area formed by every 3 points within the 4 points used to compute the homography is greater than this threshold. If the area is smaller, we are in a degenerate case. |
Definition at line 379 of file vpHomographyRansac.cpp.
References data, and vpRansac< vpTransformation >::ransac().
|
static |
From couples of matched points 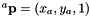 in image a and
in image a and 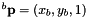 in image b with homogeneous coordinates, computes the homography matrix by resolving
in image b with homogeneous coordinates, computes the homography matrix by resolving 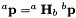 using a robust estimation scheme.
using a robust estimation scheme.
This method is to compare to DLT() except that here a robust estimator is used to reject couples of points that are considered as outliers.
At least 4 couples of points are needed.
| xb,yb | : Coordinates vector of matched points in image b. These coordinates are expressed in meters. |
| xa,ya | : Coordinates vector of matched points in image a. These coordinates are expressed in meters. |
| aHb | : Estimated homography that relies the transformation from image a to image b. |
| inliers | : Vector that indicates if a matched point is an inlier (true) or an outlier (false). |
| residual | : Global residual computed as 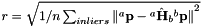 with with  the number of inliers. the number of inliers. |
| weights_threshold | : Threshold applied on the weights updated during the robust estimation and used to consider if a point is an outlier or an inlier. Values should be in [0:1]. A couple of matched points that have a weight lower than this threshold is considered as an outlier. A value equal to zero indicates that all the points are inliers. |
| niter | : Number of iterations of the estimation process. |
| normalization | : When set to true, the coordinates of the points are normalized. The normalization carried out is the one preconized by Hartley. |
Definition at line 603 of file vpHomography.cpp.
References data, vpException::dimensionError, vpException::fatalError, vpRobust::MEstimator(), vpMatrix::pseudoInverse(), vpRobust::setIteration(), and vpRobust::TUKEY.
| void vpHomography::save | ( | std::ofstream & | f | ) | const |
Save an homography in a file.
Definition at line 250 of file vpHomography.cpp.
References vpException::ioError.
| void vpHomography::setIdentity | ( | ) |
Set the homography as identity transformation.
Definition at line 517 of file vpHomography.cpp.
Referenced by vpHomography().
|
friend |
std::cout a matrix
Definition at line 751 of file vpHomography.cpp.
| double* vpHomography::data |
Data array.
Definition at line 182 of file vpHomography.h.
Referenced by operator*(), operator/(), operator/=(), ransac(), robust(), vpHomography(), and ~vpHomography().