 |
ViSP
2.8.0
|
 |
ViSP
2.8.0
|
#include <vpExponentialMap.h>
Static Public Member Functions | |
| static vpHomogeneousMatrix | direct (const vpColVector &v) |
| static vpHomogeneousMatrix | direct (const vpColVector &v, const double &delta_t) |
| static vpColVector | inverse (const vpHomogeneousMatrix &M) |
| static vpColVector | inverse (const vpHomogeneousMatrix &M, const double &delta_t) |
Direct or inverse exponential map computation.
The displacement is represented as an homogeneous matrix (vpHomogeneousMatrix). Velocities are represented as a ![$ [{\bf t}, {\bf \theta u} ]^t $](form_326.png) 6 dimension vector where
6 dimension vector where 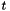 is a translation vector (see vpTranslationVector) and
is a translation vector (see vpTranslationVector) and 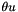 a rotation vector (see vpThetaUVector).
a rotation vector (see vpThetaUVector).
Definition at line 81 of file vpExponentialMap.h.
|
static |
Compute the exponential map. The inverse function is inverse(). The sampling time is here set to 1 second. To use an other value you should use direct(const vpColVector &, const float &).
| v | : Instantaneous velocity represented by a 6 dimension vector ![$ [{\bf t}, {\bf \theta u}]^t $](form_317.png) where where 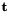 is a translation vector and is a translation vector and 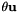 is a rotation vector (see vpThetaUVector). is a rotation vector (see vpThetaUVector). ![$ {\bf v} = [t_x, t_y, t_z, {\theta u}_x, {\theta u}_y, {\theta u}_z] $](form_320.png) (see vpTranslationVector and vpThetaUVector). (see vpTranslationVector and vpThetaUVector). |
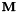 computed from an instantaneous velocity
computed from an instantaneous velocity 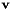 . If
. If 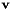 is expressed in frame c,
is expressed in frame c, 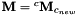 .
.Definition at line 65 of file vpExponentialMap.cpp.
Referenced by vpHomography::computeDisplacement(), vpMbEdgeKltTracker::computeVVS(), vpMbKltTracker::computeVVS(), vpMbEdgeTracker::computeVVS(), vpPose::poseVirtualVS(), vpPose::poseVirtualVSrobust(), vpRobotCamera::setVelocity(), and vpSimulatorCamera::setVelocity().
|
static |
Compute the exponential map. The inverse function is inverse().
| v | : Instantaneous velocity represented by a 6 dimension vector ![$ [{\bf t}, {\bf \theta u}]^t $](form_317.png) where where 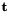 is a translation vector and is a translation vector and 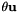 is a rotation vector (see vpThetaUVector). is a rotation vector (see vpThetaUVector). ![$ {\bf v} = [t_x, t_y, t_z, {\theta u}_x, {\theta u}_y, {\theta u}_z] $](form_320.png) (see vpTranslationVector and vpThetaUVector). (see vpTranslationVector and vpThetaUVector). |
| delta_t | : Sampling time 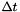 . Time during which the velocity v is applied. . Time during which the velocity v is applied. |
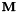 computed from an instantaneous velocity
computed from an instantaneous velocity 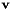 . If
. If 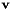 is expressed in frame c,
is expressed in frame c, 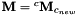 .
.Definition at line 90 of file vpExponentialMap.cpp.
References vpRotationMatrix::buildFrom(), vpHomogeneousMatrix::insert(), vpMath::mcosc(), vpMath::msinc(), and vpMath::sinc().
|
static |
Compute an instantaneous velocity from an homogeneous matrix. The inverse function is the exponential map, see direct().
| M | : An homogeneous matrix corresponding to a displacement. |
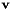 represented by a 6 dimension vector
represented by a 6 dimension vector ![$ [{\bf t}, {\bf \theta u}]^t $](form_317.png) where
where 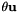 is a rotation vector (see vpThetaUVector) and
is a rotation vector (see vpThetaUVector) and 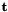 is a translation vector:
is a translation vector: ![$ {\bf v} = [t_x, t_y, t_z, {\theta u}_x, {\theta u}_y, {\theta u}_z] $](form_320.png) (see vpTranslationVector and vpThetaUVector).
(see vpTranslationVector and vpThetaUVector).Definition at line 218 of file vpExponentialMap.cpp.
Referenced by vpRobotBiclops::getDisplacement(), vpRobotAfma4::getVelocity(), vpRobotAfma6::getVelocity(), vpRobotViper850::getVelocity(), and vpRobotViper650::getVelocity().
|
static |
Compute an instantaneous velocity from an homogeneous matrix. The inverse function is the exponential map, see direct().
| M | : An homogeneous matrix corresponding to a displacement. |
| delta_t | : Sampling time 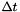 . Time during which the displacement is applied. . Time during which the displacement is applied. |
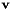 represented by a 6 dimension vector
represented by a 6 dimension vector ![$ [{\bf t}, {\bf \theta u}]^t $](form_317.png) where
where 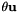 is a rotation vector (see vpThetaUVector) and
is a rotation vector (see vpThetaUVector) and 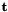 is a translation vector:
is a translation vector: ![$ {\bf v} = [t_x, t_y, t_z, {\theta u}_x, {\theta u}_y, {\theta u}_z] $](form_320.png) (see vpTranslationVector and vpThetaUVector).
(see vpTranslationVector and vpThetaUVector).Definition at line 242 of file vpExponentialMap.cpp.
References vpThetaUVector::buildFrom(), vpHomogeneousMatrix::extract(), vpMath::mcosc(), vpMath::msinc(), and vpMath::sinc().