Introduction
The "gold-standard" solution to the PnP consists in estimating the six parameters of the transformation cTw by minimizing the forward projection error using a Gauss-Newton approach. A complete derivation of this problem is given in [2].
Source code
The following source code that uses OpenCV is also available in pose-gauss-newton-opencv.cpp file. It allows to compute the pose of the camera from points.
#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/calib3d/calib3d.hpp>
void exponential_map(const cv::Mat &v, cv::Mat &dt, cv::Mat &dR)
{
double vx = v.at<double>(0,0);
double vy = v.at<double>(1,0);
double vz = v.at<double>(2,0);
double vtux = v.at<double>(3,0);
double vtuy = v.at<double>(4,0);
double vtuz = v.at<double>(5,0);
cv::Mat tu = (cv::Mat_<double>(3,1) << vtux, vtuy, vtuz);
cv::Rodrigues(tu, dR);
double theta = sqrt(tu.dot(tu));
double sinc = (fabs(theta) < 1.0e-8) ? 1.0 : sin(theta) / theta;
double mcosc = (fabs(theta) < 2.5e-4) ? 0.5 : (1.-cos(theta)) / theta / theta;
double msinc = (fabs(theta) < 2.5e-4) ? (1./6.) : (1.-sin(theta)/theta) / theta / theta;
dt.at<double>(0,0) = vx*(sinc + vtux*vtux*msinc)
+ vy*(vtux*vtuy*msinc - vtuz*mcosc)
+ vz*(vtux*vtuz*msinc + vtuy*mcosc);
dt.at<double>(1,0) = vx*(vtux*vtuy*msinc + vtuz*mcosc)
+ vy*(sinc + vtuy*vtuy*msinc)
+ vz*(vtuy*vtuz*msinc - vtux*mcosc);
dt.at<double>(2,0) = vx*(vtux*vtuz*msinc - vtuy*mcosc)
+ vy*(vtuy*vtuz*msinc + vtux*mcosc)
+ vz*(sinc + vtuz*vtuz*msinc);
}
void pose_gauss_newton(const std::vector< cv::Point3d > &wX,
const std::vector< cv::Point2d > &x,
cv::Mat &ctw, cv::Mat &cRw)
{
int npoints = (int)wX.size();
cv::Mat J(2*npoints, 6, CV_64FC1);
cv::Mat cX;
double lambda = 0.25;
cv::Mat err, sd(2*npoints, 1, CV_64FC1), s(2*npoints, 1, CV_64FC1);
cv::Mat xq(npoints*2, 1, CV_64FC1);
cv::Mat xn(npoints*2, 1, CV_64FC1);
double residual=0, residual_prev;
cv::Mat Jp;
for (int i = 0; i < x.size(); i ++) {
xn.at<double>(i*2,0) = x[i].x;
xn.at<double>(i*2+1,0) = x[i].y;
}
do {
for (int i = 0; i < npoints; i++) {
cX = cRw * cv::Mat(wX[i]) + ctw;
double Xi = cX.at<double>(0,0);
double Yi = cX.at<double>(1,0);
double Zi = cX.at<double>(2,0);
double xi = Xi / Zi;
double yi = Yi / Zi;
xq.at<double>(i*2,0) = xi;
xq.at<double>(i*2+1,0) = yi;
J.at<double>(i*2,0) = -1 / Zi;
J.at<double>(i*2,1) = 0;
J.at<double>(i*2,2) = xi / Zi;
J.at<double>(i*2,3) = xi * yi;
J.at<double>(i*2,4) = -(1 + xi * xi);
J.at<double>(i*2,5) = yi;
J.at<double>(i*2+1,0) = 0;
J.at<double>(i*2+1,1) = -1 / Zi;
J.at<double>(i*2+1,2) = yi / Zi;
J.at<double>(i*2+1,3) = 1 + yi * yi;
J.at<double>(i*2+1,4) = -xi * yi;
J.at<double>(i*2+1,5) = -xi;
}
cv::Mat e_q = xq - xn;
cv::Mat Jp = J.inv(cv::DECOMP_SVD);
cv::Mat dq = -lambda * Jp * e_q;
cv::Mat dctw(3,1,CV_64FC1), dcRw(3,3,CV_64FC1);
exponential_map(dq, dctw, dcRw);
cRw = dcRw.t() * cRw;
ctw = dcRw.t() * (ctw - dctw);
residual_prev = residual;
residual = e_q.dot(e_q);
} while (fabs(residual - residual_prev) > 0);
}
int main()
{
std::vector< cv::Point3d > wX;
std::vector< cv::Point2d > x;
cv::Mat ctw_truth = (cv::Mat_<double>(3,1) << -0.1, 0.1, 0.5);
cv::Mat crw_truth = (cv::Mat_<double>(3,1) << CV_PI/180*(5), CV_PI/180*(0), CV_PI/180*(45));
cv::Mat cRw_truth(3,3,CV_64FC1);
cv::Rodrigues(crw_truth, cRw_truth);
double L = 0.2;
wX.push_back( cv::Point3d( -L, -L, 0) );
wX.push_back( cv::Point3d( 2*L, -L, 0) );
wX.push_back( cv::Point3d( L, L, 0) );
wX.push_back( cv::Point3d( -L, L, 0) );
for(int i = 0; i < wX.size(); i++) {
cv::Mat cX = cRw_truth*cv::Mat(wX[i]) + ctw_truth;
x.push_back( cv::Point2d( cX.at<double>(0, 0)/cX.at<double>(2, 0),
cX.at<double>(1, 0)/cX.at<double>(2, 0) ) );
}
cv::Mat ctw = (cv::Mat_<double>(3,1) << -0.05, 0.05, 0.45);
cv::Mat crw = (cv::Mat_<double>(3,1) << CV_PI/180*(1), CV_PI/180*(0), CV_PI/180*(35));
cv::Mat cRw = cv::Mat::eye(3, 3, CV_64FC1);
cv::Rodrigues(crw, cRw);
pose_gauss_newton(wX, x, ctw, cRw);
std::cout << "ctw (ground truth):\n" << ctw_truth << std::endl;
std::cout << "ctw (from non linear method):\n" << ctw << std::endl;
std::cout << "cRw (ground truth):\n" << cRw_truth << std::endl;
std::cout << "cRw (from non linear method):\n" << cRw << std::endl;
return 0;
}
Source code explained
First of all we include OpenCV headers that are requested to manipulate vectors and matrices and also to compute the exponential map.
#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/calib3d/calib3d.hpp>
Then we introduce the function that does the pose estimation. It takes as input parameters 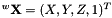 the 3D coordinates of the points in the world frame and
the 3D coordinates of the points in the world frame and 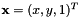 their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.
their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.
void pose_gauss_newton(const std::vector< cv::Point3d > &wX,
const std::vector< cv::Point2d > &x,
cv::Mat &ctw, cv::Mat &cRw)
The implementation of the iterative Gauss-Newton minimization process is done next. First, we create the variables used by the algorithm. Since the algorithm needs an initialization, we set an initial value in cTw not to far from the solution. Such an initialization could be done using Pose from Direct Linear Transform method of Pose from Dementhon's POSIT method approaches. Finally, the estimation is iterated.
int npoints = (int)wX.size();
cv::Mat J(2*npoints, 6, CV_64FC1);
cv::Mat cX;
double lambda = 0.25;
cv::Mat err, sd(2*npoints, 1, CV_64FC1), s(2*npoints, 1, CV_64FC1);
cv::Mat xq(npoints*2, 1, CV_64FC1);
cv::Mat xn(npoints*2, 1, CV_64FC1);
double residual=0, residual_prev;
cv::Mat Jp;
for (int i = 0; i < x.size(); i ++) {
xn.at<double>(i*2,0) = x[i].x;
xn.at<double>(i*2+1,0) = x[i].y;
}
do {
for (int i = 0; i < npoints; i++) {
cX = cRw * cv::Mat(wX[i]) + ctw;
double Xi = cX.at<double>(0,0);
double Yi = cX.at<double>(1,0);
double Zi = cX.at<double>(2,0);
double xi = Xi / Zi;
double yi = Yi / Zi;
xq.at<double>(i*2,0) = xi;
xq.at<double>(i*2+1,0) = yi;
J.at<double>(i*2,0) = -1 / Zi;
J.at<double>(i*2,1) = 0;
J.at<double>(i*2,2) = xi / Zi;
J.at<double>(i*2,3) = xi * yi;
J.at<double>(i*2,4) = -(1 + xi * xi);
J.at<double>(i*2,5) = yi;
J.at<double>(i*2+1,0) = 0;
J.at<double>(i*2+1,1) = -1 / Zi;
J.at<double>(i*2+1,2) = yi / Zi;
J.at<double>(i*2+1,3) = 1 + yi * yi;
J.at<double>(i*2+1,4) = -xi * yi;
J.at<double>(i*2+1,5) = -xi;
}
cv::Mat e_q = xq - xn;
cv::Mat Jp = J.inv(cv::DECOMP_SVD);
cv::Mat dq = -lambda * Jp * e_q;
cv::Mat dctw(3,1,CV_64FC1), dcRw(3,3,CV_64FC1);
exponential_map(dq, dctw, dcRw);
cRw = dcRw.t() * cRw;
ctw = dcRw.t() * (ctw - dctw);
residual_prev = residual;
residual = e_q.dot(e_q);
} while (fabs(residual - residual_prev) > 0);
When the residual obtained between two successive iterations can be neglected, we can exit the while loop and return.
Finally we define the main function in which we will initialize the input data before calling the previous function and computing the pose using non linear Gauss-Newton approach.
First in the main we create the data structures that will contain the 3D points coordinates wX in the world frame, their coordinates in the camera frame cX and their coordinates in the image plane x obtained after prerspective projection. Note here that at least 4 non coplanar points are requested to estimate the pose.
std::vector< cv::Point3d > wX;
std::vector< cv::Point2d > x;
For our simulation we then initialize the input data from a ground truth pose with the translation in ctw_truth and the rotation matrix in cRw_truth. For each point we set in wX[i] the 3D coordinates in the world frame (wX, wY, wZ, 1) and compute in cX their 3D coordinates (cX, cY, cZ, 1) in the camera frame. Then in x[i] we update their coordinates (x, y) in the image plane, obtained by perspective projection.
cv::Mat ctw_truth = (cv::Mat_<double>(3,1) << -0.1, 0.1, 0.5);
cv::Mat crw_truth = (cv::Mat_<double>(3,1) << CV_PI/180*(5), CV_PI/180*(0), CV_PI/180*(45));
cv::Mat cRw_truth(3,3,CV_64FC1);
cv::Rodrigues(crw_truth, cRw_truth);
double L = 0.2;
wX.push_back( cv::Point3d( -L, -L, 0) );
wX.push_back( cv::Point3d( 2*L, -L, 0) );
wX.push_back( cv::Point3d( L, L, 0) );
wX.push_back( cv::Point3d( -L, L, 0) );
for(int i = 0; i < wX.size(); i++) {
cv::Mat cX = cRw_truth*cv::Mat(wX[i]) + ctw_truth;
x.push_back( cv::Point2d( cX.at<double>(0, 0)/cX.at<double>(2, 0),
cX.at<double>(1, 0)/cX.at<double>(2, 0) ) );
}
From here we have initialized 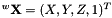 and
and 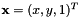 . Since the non-linear minimization method requires a initial value of the pose to estimate we initialize
. Since the non-linear minimization method requires a initial value of the pose to estimate we initialize 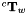 not so far from the solution, in ctw for the translation vector and in cRw for the rotation vector.
not so far from the solution, in ctw for the translation vector and in cRw for the rotation vector.
cv::Mat ctw = (cv::Mat_<double>(3,1) << -0.05, 0.05, 0.45);
cv::Mat crw = (cv::Mat_<double>(3,1) << CV_PI/180*(1), CV_PI/180*(0), CV_PI/180*(35));
cv::Mat cRw = cv::Mat::eye(3, 3, CV_64FC1);
cv::Rodrigues(crw, cRw);
- Note
- In a real application this initialization has to be done using:
We are now ready to call the function that does the pose estimation.
pose_gauss_newton(wX, x, ctw, cRw);
Resulting pose estimation
If you run the previous code, it we produce the following result that shows that the estimated pose is equal to the ground truth one used to generate the input data:
ctw (ground truth):
[-0.1;
0.1;
0.5]
ctw (from non linear method):
[-0.09999999999999963;
0.1000000000000001;
0.5000000000000006]
cRw (ground truth):
[0.7072945483755065, -0.7061704379962989, 0.03252282795827704;
0.7061704379962989, 0.7036809008245869, -0.07846338199958876;
0.03252282795827704, 0.07846338199958876, 0.9963863524490802]
cRw (from non linear method):
[0.7072945483755072, -0.7061704379962995, 0.03252282795827719;
0.7061704379962994, 0.7036809008245862, -0.07846338199958869;
0.03252282795827711, 0.07846338199958879, 0.9963863524490796]
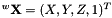 the 3D coordinates of the points in the world frame and
the 3D coordinates of the points in the world frame and 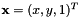 their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.
their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.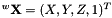 and
and 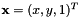 . Since the non-linear minimization method requires a initial value of the pose to estimate we initialize
. Since the non-linear minimization method requires a initial value of the pose to estimate we initialize 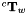 not so far from the solution, in ctw for the translation vector and in cRw for the rotation vector.
not so far from the solution, in ctw for the translation vector and in cRw for the rotation vector. 1.8.14
1.8.14