Introduction
Although PnP is intrinsically a non-linear problem, a simple solution known as Direct Linear Transform (DLT) [4] [7] based on the resolution of a linear system can be considered.
Source code
The following source code that uses ViSP is also available in pose-dlt-visp.cpp file. It allows to compute the pose of the camera from points.
#include <visp/vpColVector.h>
#include <visp/vpHomogeneousMatrix.h>
#include <visp/vpMatrix.h>
vpHomogeneousMatrix pose_dlt(const std::vector< vpColVector > &wX, const std::vector< vpColVector > &x)
{
int npoints = (int)wX.size();
vpMatrix A(2*npoints, 12, 0.);
for(int i = 0; i < npoints; i++) {
A[2*i][0] = wX[i][0];
A[2*i][1] = wX[i][1];
A[2*i][2] = wX[i][2];
A[2*i][3] = 1;
A[2*i+1][4] = wX[i][0];
A[2*i+1][5] = wX[i][1];
A[2*i+1][6] = wX[i][2];
A[2*i+1][7] = 1;
A[2*i][8] = -x[i][0] * wX[i][0];
A[2*i][9] = -x[i][0] * wX[i][1];
A[2*i][10] = -x[i][0] * wX[i][2];
A[2*i][11] = -x[i][0];
A[2*i+1][8] = -x[i][1] * wX[i][0];
A[2*i+1][9] = -x[i][1] * wX[i][1];
A[2*i+1][10] = -x[i][1] * wX[i][2];
A[2*i+1][11] = -x[i][1];
}
vpColVector D;
vpMatrix V;
A.svd(D, V);
double smallestSv = D[0];
unsigned int indexSmallestSv = 0 ;
for (unsigned int i = 1; i < D.size(); i++) {
if ((D[i] < smallestSv) ) {
smallestSv = D[i];
indexSmallestSv = i;
}
}
#if VISP_VERSION_INT >= VP_VERSION_INT(2, 10, 0)
vpColVector h = V.getCol(indexSmallestSv);
#else
vpColVector h = V.column(indexSmallestSv + 1);
#endif
if (h[11] < 0)
h *=-1;
double norm = sqrt(vpMath::sqr(h[8]) + vpMath::sqr(h[9]) + vpMath::sqr(h[10]));
h /= norm;
vpHomogeneousMatrix cTw;
for (int i = 0 ; i < 3 ; i++)
for (int j = 0 ; j < 4 ; j++)
cTw[i][j] = h[4*i+j];
return cTw;
}
int main()
{
int npoints = 6;
std::vector< vpColVector > wX(npoints);
std::vector< vpColVector > x(npoints);
for (int i = 0; i < npoints; i++) {
wX[i].resize(4);
x[i].resize(3);
}
vpHomogeneousMatrix cTw_truth(-0.1, 0.1, 1.2, vpMath::rad(5), vpMath::rad(0), vpMath::rad(45));
double L = 0.2;
wX[0][0] = -L; wX[0][1] = -L; wX[0][2] = 0; wX[0][3] = 1;
wX[1][0] = 2*L; wX[1][1] = -L; wX[1][2] = 0.2; wX[1][3] = 1;
wX[2][0] = L; wX[2][1] = L; wX[2][2] = 0.2; wX[2][3] = 1;
wX[3][0] = -L; wX[3][1] = L; wX[3][2] = 0; wX[3][3] = 1;
wX[4][0] = -2*L; wX[4][1] = L; wX[4][2] = 0; wX[4][3] = 1;
wX[5][0] = 0; wX[5][1] = 0; wX[5][2] = 0.5; wX[5][3] = 1;
for(int i = 0; i < npoints; i++) {
vpColVector cX = cTw_truth * wX[i];
x[i][0] = cX[0] / cX[2];
x[i][1] = cX[1] / cX[2];
x[i][2] = 1;
}
vpHomogeneousMatrix cTw = pose_dlt(wX, x);
std::cout << "cTw (ground truth):\n" << cTw_truth << std::endl;
std::cout << "cTw (computed with DLT):\n" << cTw << std::endl;
return 0;
}
Source code explained
First of all we include the header of the files that are requested to manipulate ViSP vectors and matrices.
#include <visp/vpColVector.h>
#include <visp/vpHomogeneousMatrix.h>
#include <visp/vpMatrix.h>
Then we introduce the function that does the pose estimation. It takes as input parameters 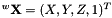 the 3D coordinates of the points in the world frame and
the 3D coordinates of the points in the world frame and 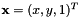 their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.
their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.
vpHomogeneousMatrix pose_dlt(const std::vector< vpColVector > &wX, const std::vector< vpColVector > &x)
The implementation of the Direct Linear Transform algorithm is done next. First, for each point we update the values of matrix A using equation (5). Then we solve the system Ah=0 using a Singular Value Decomposition of A. Finaly, we determine the smallest eigen value that allows to identify the eigen vector that corresponds to the solution.
int npoints = (int)wX.size();
vpMatrix A(2*npoints, 12, 0.);
for(int i = 0; i < npoints; i++) {
A[2*i][0] = wX[i][0];
A[2*i][1] = wX[i][1];
A[2*i][2] = wX[i][2];
A[2*i][3] = 1;
A[2*i+1][4] = wX[i][0];
A[2*i+1][5] = wX[i][1];
A[2*i+1][6] = wX[i][2];
A[2*i+1][7] = 1;
A[2*i][8] = -x[i][0] * wX[i][0];
A[2*i][9] = -x[i][0] * wX[i][1];
A[2*i][10] = -x[i][0] * wX[i][2];
A[2*i][11] = -x[i][0];
A[2*i+1][8] = -x[i][1] * wX[i][0];
A[2*i+1][9] = -x[i][1] * wX[i][1];
A[2*i+1][10] = -x[i][1] * wX[i][2];
A[2*i+1][11] = -x[i][1];
}
vpColVector D;
vpMatrix V;
A.svd(D, V);
double smallestSv = D[0];
unsigned int indexSmallestSv = 0 ;
for (unsigned int i = 1; i < D.size(); i++) {
if ((D[i] < smallestSv) ) {
smallestSv = D[i];
indexSmallestSv = i;
}
}
#if VISP_VERSION_INT >= VP_VERSION_INT(2, 10, 0)
vpColVector h = V.getCol(indexSmallestSv);
#else
vpColVector h = V.column(indexSmallestSv + 1);
#endif
if (h[11] < 0)
h *=-1;
double norm = sqrt(vpMath::sqr(h[8]) + vpMath::sqr(h[9]) + vpMath::sqr(h[10]));
h /= norm;
From now the resulting eigen vector h that corresponds to the minimal eigen value of matrix A is used to update the homogenous transformation cTw:
vpHomogeneousMatrix cTw;
for (int i = 0 ; i < 3 ; i++)
for (int j = 0 ; j < 4 ; j++)
cTw[i][j] = h[4*i+j];
Finally we define the main function in which we will initialize the input data before calling the previous function and computing the pose using DLT algorithm.
First in the main we create the data structures that will contain the 3D points coordinates wX in the world frame, their coordinates in the image plane x obtained after prerspective projection. Note here that at least 4 non coplanar points are requested to estimate the pose.
int npoints = 6;
std::vector< vpColVector > wX(npoints);
std::vector< vpColVector > x(npoints);
for (int i = 0; i < npoints; i++) {
wX[i].resize(4);
x[i].resize(3);
}
For our simulation we then initialize the input data from a ground truth pose cTw_truth. For each point we set in wX[i] the 3D coordinates in the world frame (wX, wY, wZ, 1) and compute in cX their 3D coordinates (cX, cY, cZ, 1) in the camera frame. Then in x[i] we update their coordinates (x, y) in the image plane, obtained by perspective projection.
vpHomogeneousMatrix cTw_truth(-0.1, 0.1, 1.2, vpMath::rad(5), vpMath::rad(0), vpMath::rad(45));
double L = 0.2;
wX[0][0] = -L; wX[0][1] = -L; wX[0][2] = 0; wX[0][3] = 1;
wX[1][0] = 2*L; wX[1][1] = -L; wX[1][2] = 0.2; wX[1][3] = 1;
wX[2][0] = L; wX[2][1] = L; wX[2][2] = 0.2; wX[2][3] = 1;
wX[3][0] = -L; wX[3][1] = L; wX[3][2] = 0; wX[3][3] = 1;
wX[4][0] = -2*L; wX[4][1] = L; wX[4][2] = 0; wX[4][3] = 1;
wX[5][0] = 0; wX[5][1] = 0; wX[5][2] = 0.5; wX[5][3] = 1;
for(int i = 0; i < npoints; i++) {
vpColVector cX = cTw_truth * wX[i];
x[i][0] = cX[0] / cX[2];
x[i][1] = cX[1] / cX[2];
x[i][2] = 1;
}
From here we have initialized 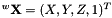 and
and 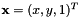 . We are now ready to call the function that does the pose estimation.
. We are now ready to call the function that does the pose estimation.
vpHomogeneousMatrix cTw = pose_dlt(wX, x);
Resulting pose estimation
If you run the previous code, it we produce the following result that shows that the estimated pose is equal to the ground truth one used to generate the input data:
cTw (ground truth):
0.7072945484 -0.706170438 0.03252282796 0.1
0.706170438 0.7036809008 -0.078463382 0.1
0.03252282796 0.078463382 0.9963863524 1.2
0 0 0 1
cTw (computed with DLT):
0.7072945484 -0.706170438 0.03252282796 0.1
0.706170438 0.7036809008 -0.078463382 0.1
0.03252282796 0.078463382 0.9963863524 1.2
0 0 0 1
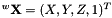 the 3D coordinates of the points in the world frame and
the 3D coordinates of the points in the world frame and 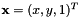 their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.
their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.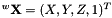 and
and 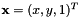 . We are now ready to call the function that does the pose estimation.
. We are now ready to call the function that does the pose estimation. 1.8.14
1.8.14