 |
Visual Servoing Platform
version 3.6.1 under development (2024-04-25)
|
 |
Visual Servoing Platform
version 3.6.1 under development (2024-04-25)
|
#include <visp3/me/vpNurbs.h>
 Inheritance diagram for vpNurbs:
Inheritance diagram for vpNurbs:Public Member Functions | |
| vpNurbs () | |
| vpNurbs (const vpNurbs &nurbs) | |
| void | get_weights (std::list< double > &list) const |
| void | set_weights (const std::list< double > &list) |
| vpImagePoint | computeCurvePoint (double u) |
| vpImagePoint * | computeCurveDersPoint (double u, unsigned int der) |
| void | curveKnotIns (double u, unsigned int s=0, unsigned int r=1) |
| void | refineKnotVectCurve (double *x, unsigned int r) |
| unsigned int | removeCurveKnot (double l_u, unsigned int l_r, unsigned int l_num, double l_TOL) |
| void | globalCurveInterp (vpList< vpMeSite > &l_crossingPoints) |
| void | globalCurveInterp (const std::list< vpImagePoint > &l_crossingPoints) |
| void | globalCurveInterp (const std::list< vpMeSite > &l_crossingPoints) |
| void | globalCurveInterp () |
| void | globalCurveApprox (vpList< vpMeSite > &l_crossingPoints, unsigned int n) |
| void | globalCurveApprox (const std::list< vpImagePoint > &l_crossingPoints, unsigned int n) |
| void | globalCurveApprox (const std::list< vpMeSite > &l_crossingPoints, unsigned int n) |
| void | globalCurveApprox (unsigned int n) |
| unsigned int | get_p () const |
| void | get_controlPoints (std::list< vpImagePoint > &list) const |
| void | get_knots (std::list< double > &list) const |
| void | get_crossingPoints (std::list< vpImagePoint > &list) const |
| void | set_p (unsigned int degree) |
| void | set_controlPoints (const std::list< vpImagePoint > &list) |
| void | set_knots (const std::list< double > &list) |
| void | set_crossingPoints (const std::list< vpImagePoint > &list) |
| unsigned int | findSpan (double u) const |
| vpBasisFunction * | computeBasisFuns (double u) const |
| vpBasisFunction ** | computeDersBasisFuns (double u, unsigned int der) const |
| vpImagePoint | computeCurvePoint (double u) const |
| vpImagePoint * | computeCurveDers (double u, unsigned int der) const |
Static Public Member Functions | |
| static vpImagePoint | computeCurvePoint (double l_u, unsigned int l_i, unsigned int l_p, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
| static vpImagePoint * | computeCurveDersPoint (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
| static void | curveKnotIns (double l_u, unsigned int l_k, unsigned int l_s, unsigned int l_r, unsigned int l_p, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
| static void | refineKnotVectCurve (double *l_x, unsigned int l_r, unsigned int l_p, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
| static unsigned int | removeCurveKnot (double l_u, unsigned int l_r, unsigned int l_num, double l_TOL, unsigned int l_s, unsigned int l_p, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
| static void | globalCurveInterp (std::vector< vpImagePoint > &l_crossingPoints, unsigned int l_p, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
| static void | globalCurveApprox (std::vector< vpImagePoint > &l_crossingPoints, unsigned int l_p, unsigned int l_n, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
| static unsigned int | findSpan (double l_u, unsigned int l_p, const std::vector< double > &l_knots) |
| static vpBasisFunction * | computeBasisFuns (double l_u, unsigned int l_i, unsigned int l_p, const std::vector< double > &l_knots) |
| static vpBasisFunction ** | computeDersBasisFuns (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, const std::vector< double > &l_knots) |
| static vpImagePoint | computeCurvePoint (double l_u, unsigned int l_i, unsigned int l_p, const std::vector< double > &l_knots, const std::vector< vpImagePoint > &l_controlPoints) |
| static vpImagePoint * | computeCurveDers (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, const std::vector< double > &l_knots, const std::vector< vpImagePoint > &l_controlPoints) |
Protected Member Functions | |
| vpMatrix | computeCurveDers (double u, unsigned int der) |
Static Protected Member Functions | |
| static vpMatrix | computeCurveDers (double l_u, unsigned int l_i, unsigned int l_p, unsigned int l_der, std::vector< double > &l_knots, std::vector< vpImagePoint > &l_controlPoints, std::vector< double > &l_weights) |
Protected Attributes | |
| std::vector< double > | weights |
Class that provides tools to compute and manipulate a Non Uniform Rational B-Spline curve.
The different parameters are :
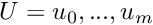 where the knots
where the knots 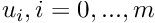 are real number such as
are real number such as 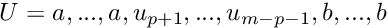 where
where 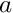 and
and 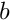 are real numbers and p is the degree of the B-Spline basis functions.
are real numbers and p is the degree of the B-Spline basis functions.The B-Spline basis functions 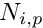 defined as :
defined as :
![]()
![\[ N_{i,p}(u) = \frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)\]](form_11.png)
where 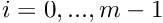 and p is the degree of the B-Spline basis functions.
and p is the degree of the B-Spline basis functions.
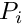 which are defined by the coordinates
which are defined by the coordinates 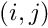 of a point in an image.
of a point in an image.It is possible to compute the coordinates of a point corresponding to the knots  (
( ![$ u \in [u_0,u_m]$](form_16.png) ) thanks to the formula :
) thanks to the formula :
![]()
You can find much more information about the B-Splines and the implementation of all the methods in the Nurbs Book.
| vpNurbs::vpNurbs | ( | ) |
Basic constructor.
The degree ![]() of the NURBS basis functions is set to 3 to compute cubic NURBS.
of the NURBS basis functions is set to 3 to compute cubic NURBS.
Definition at line 49 of file vpNurbs.cpp.
| vpNurbs::vpNurbs | ( | const vpNurbs & | nurbs | ) |
Copy constructor.
Definition at line 51 of file vpNurbs.cpp.
|
staticinherited |
Compute the nonvanishing basis functions at ![]() which is in the
which is in the ![]() th knot interval. All the basis functions are stored in an array such as :
th knot interval. All the basis functions are stored in an array such as :
N = ![]() ,
, ![]() ,
, ![]() , ... ,
, ... , ![]() , ...,
, ..., ![]() , ... ,
, ... , ![]() , ... ,
, ... , ![]()
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
Definition at line 142 of file vpBSpline.cpp.
Referenced by vpBSpline::computeBasisFuns(), vpBSpline::computeCurvePoint(), computeCurvePoint(), globalCurveApprox(), and globalCurveInterp().
|
inherited |
Compute the nonvanishing basis functions at  . All the basis functions are stored in an array such as :
. All the basis functions are stored in an array such as :
N = ![]() ,
, ![]() ,
, ![]() , ... ,
, ... , ![]() , ...,
, ..., ![]() , ... ,
, ... , ![]() , ... ,
, ... , ![]()
where i the number of the knot interval in which  lies.
lies.
| u | : A real number which is between the extremities of the knot vector |
 . The size of the array is
. The size of the array is Definition at line 193 of file vpBSpline.cpp.
References vpBSpline::computeBasisFuns(), and vpBSpline::findSpan().
|
staticinherited |
Compute the kth derivatives of ![]() for
for ![]() .
.
The formula used is the following :
![]()
where 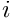 is the knot interval number in which
is the knot interval number in which  lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
Definition at line 445 of file vpBSpline.cpp.
References vpBSpline::computeDersBasisFuns(), vpImagePoint::set_i(), vpImagePoint::set_ij(), vpImagePoint::set_j(), and vpTRACE.
|
staticprotected |
This function is used in the computeCurveDersPoint method.
Compute the kth derivatives of ![]() for
for ![]() .
.
The formula used is the following :
![]()
where 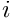 is the knot interval number in which
is the knot interval number in which  lies,
lies, ![]() is the degree of the NURBS basis function and
is the degree of the NURBS basis function and ![]() contains the control points and the associated weights.
contains the control points and the associated weights.
| l_u | : A real number which is between the extremities of the knot vector. |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the NURBS basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector. |
| l_controlPoints | : the list of control points. |
| l_weights | : the list of weights. |
Definition at line 102 of file vpNurbs.cpp.
References vpBSpline::computeDersBasisFuns().
Referenced by computeCurveDersPoint().
|
protected |
This function is used in the computeCurveDersPoint method.
Compute the kth derivatives of ![]() for
for ![]() .
.
The formula used is the following :
![]()
where 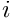 is the knot interval number in which
is the knot interval number in which  lies,
lies, ![]() is the degree of the NURBS basis function and
is the degree of the NURBS basis function and ![]() contains the control points and the associated weights.
contains the control points and the associated weights.
| u | : A real number which is between the extremities of the knot vector |
| der | : The last derivative to be computed. |
Definition at line 130 of file vpNurbs.cpp.
References vpBSpline::computeDersBasisFuns(), and weights.
|
inherited |
Compute the kth derivatives of ![]() for
for ![]() .
.
The formula used is the following :
![]()
where 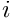 is the knot interval number in which
is the knot interval number in which  lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| u | : A real number which is between the extremities of the knot vector |
| der | : The last derivative to be computed. |
Definition at line 492 of file vpBSpline.cpp.
References vpBSpline::computeDersBasisFuns(), vpImagePoint::set_i(), vpImagePoint::set_ij(), vpImagePoint::set_j(), and vpTRACE.
|
static |
Compute the kth derivatives of ![]() for
for ![]() .
.
To see how the derivatives are computed refers to the Nurbs book.
| l_u | : A real number which is between the extremities of the knot vector. |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the NURBS basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector. |
| l_controlPoints | : the list of control points. |
| l_weights | : the list of weights. |
Definition at line 153 of file vpNurbs.cpp.
References vpMath::comb(), computeCurveDers(), vpImagePoint::get_i(), vpImagePoint::get_j(), vpImagePoint::set_i(), vpImagePoint::set_ij(), and vpImagePoint::set_j().
Referenced by computeCurveDersPoint(), vpMeNurbs::localReSample(), vpMeNurbs::sample(), vpMeNurbs::seekExtremities(), vpMeNurbs::seekExtremitiesCanny(), and vpMeNurbs::updateDelta().
| vpImagePoint * vpNurbs::computeCurveDersPoint | ( | double | u, |
| unsigned int | der | ||
| ) |
Compute the kth derivatives of ![]() for
for ![]() .
.
To see how the derivatives are computed refers to the Nurbs book.
| u | : A real number which is between the extremities of the knot vector |
| der | : The last derivative to be computed. |
Definition at line 184 of file vpNurbs.cpp.
References computeCurveDersPoint(), vpBSpline::findSpan(), and weights.
|
staticinherited |
Compute the coordinates of a point ![]() corresponding to the knot
corresponding to the knot  .
.
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
return the coordinates of a point corresponding to the knot  .
.
Definition at line 375 of file vpBSpline.cpp.
References vpBSpline::computeBasisFuns(), vpImagePoint::set_i(), and vpImagePoint::set_j().
|
static |
Compute the coordinates of a point ![]() corresponding to the knot
corresponding to the knot  .
.
| l_u | : A real number which is between the extremities of the knot vector. |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the NURBS basis functions. |
| l_knots | : The knot vector. |
| l_controlPoints | : the list of control points. |
| l_weights | : the list of weights. |
 .
. Definition at line 53 of file vpNurbs.cpp.
References vpBSpline::computeBasisFuns(), vpImagePoint::set_i(), and vpImagePoint::set_j().
Referenced by vpMeNurbs::display(), vpMeNurbs::localReSample(), vpMeNurbs::seekExtremitiesCanny(), vpMeNurbs::track(), and vpMeNurbs::updateDelta().
| vpImagePoint vpNurbs::computeCurvePoint | ( | double | u | ) |
Compute the coordinates of a point ![]() corresponding to the knot
corresponding to the knot  .
.
| u | : A real number which is between the extremities of the knot vector |
return the coordinates of a point corresponding to the knot  .
.
Definition at line 78 of file vpNurbs.cpp.
References vpBSpline::computeBasisFuns(), vpImagePoint::set_i(), vpImagePoint::set_j(), and weights.
|
inherited |
Compute the coordinates of a point ![]() corresponding to the knot
corresponding to the knot  .
.
| u | : A real number which is between the extremities of the knot vector |
return the coordinates of a point corresponding to the knot  .
.
Definition at line 404 of file vpBSpline.cpp.
References vpBSpline::computeBasisFuns(), vpImagePoint::set_i(), and vpImagePoint::set_j().
|
staticinherited |
Compute the nonzero basis functions and their derivatives until the ![]() th derivative. All the functions are computed at l_u.
th derivative. All the functions are computed at l_u.
The result is given as an array of size l_der+1 x l_p+1. The kth line corresponds to the kth basis functions derivatives.
The formula to compute the kth derivative at  is :
is :
![]()
where 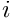 is the knot interval number in which
is the knot interval number in which  lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| l_u | : A real number which is between the extremities of the knot vector |
| l_i | : the number of the knot interval in which |
| l_p | : Degree of the B-Spline basis functions. |
| l_der | : The last derivative to be computed. |
| l_knots | : The knot vector |
Example : return[0] is the list of the 0th derivatives ie the basis functions. return[k] is the list of the kth derivatives.
Definition at line 228 of file vpBSpline.cpp.
References vpTRACE.
Referenced by vpBSpline::computeCurveDers(), computeCurveDers(), and vpBSpline::computeDersBasisFuns().
|
inherited |
Compute the nonzero basis functions and their derivatives until the ![]() th derivative. All the functions are computed at u.
th derivative. All the functions are computed at u.
The result is given as an array of size der+1 x p+1. The kth line corresponds to the kth basis functions derivatives.
The formula to compute the kth derivative at  is :
is :
![]()
where 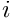 is the knot interval number in which
is the knot interval number in which  lies and
lies and ![]() is the degree of the B-Spline basis function.
is the degree of the B-Spline basis function.
| u | : A real number which is between the extremities of the knot vector |
| der | : The last derivative to be computed. |
Example : return[0] is the list of the 0th derivatives ie the basis functions. return[k] is the list of the kth derivatives.
Definition at line 358 of file vpBSpline.cpp.
References vpBSpline::computeDersBasisFuns(), and vpBSpline::findSpan().
|
static |
Insert ![]() times a knot in the
times a knot in the ![]() th interval of the knot vector. The inserted knot
th interval of the knot vector. The inserted knot ![]() has multiplicity
has multiplicity ![]() .
.
Of course the knot vector changes. But The list of control points and the list of the associated weights change too.
| l_u | : A real number which is between the extremities of the knot vector and which has to be inserted. |
| l_k | : The number of the knot interval in which |
| l_s | : Multiplicity of |
| l_r | : Number of times |
| l_p | : Degree of the NURBS basis functions. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
| l_weights | : the list of weights. |
Definition at line 191 of file vpNurbs.cpp.
References vpMatrix::insert(), and vpImagePoint::set_ij().
Referenced by curveKnotIns().
| void vpNurbs::curveKnotIns | ( | double | u, |
| unsigned int | s = 0, |
||
| unsigned int | r = 1 |
||
| ) |
Insert ![]() times a knot in the
times a knot in the ![]() th interval of the knot vector. The inserted knot
th interval of the knot vector. The inserted knot  has multiplicity
has multiplicity 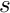 .
.
Of course the knot vector changes. But The list of control points and the list of the associated weights change too.
| u | : A real number which is between the extremities of the knot vector and which has to be inserted. |
| s | : Multiplicity of |
| r | : Number of times |
Definition at line 243 of file vpNurbs.cpp.
References curveKnotIns(), vpBSpline::findSpan(), and weights.
|
staticinherited |
Find the knot interval in which the parameter ![]() lies. Indeed
lies. Indeed ![]()
Example : The knot vector is the following ![]() with
with ![]() is equal to 1.
is equal to 1.
| l_u | : The knot whose knot interval is seeked. |
| l_p | : Degree of the B-Spline basis functions. |
| l_knots | : The knot vector |
Definition at line 79 of file vpBSpline.cpp.
References vpMath::maximum(), and vpMath::round().
Referenced by vpBSpline::computeBasisFuns(), computeCurveDersPoint(), vpBSpline::computeDersBasisFuns(), curveKnotIns(), vpBSpline::findSpan(), globalCurveApprox(), globalCurveInterp(), and refineKnotVectCurve().
|
inherited |
Find the knot interval in which the parameter  lies. Indeed
lies. Indeed ![]()
Example : The knot vector is the following ![]() with
with ![]() is equal to 1.
is equal to 1.
 equal to 0.5 the method will return 1.
equal to 0.5 the method will return 1. equal to 2.5 the method will return 3.
equal to 2.5 the method will return 3. equal to 3 the method will return 3.
equal to 3 the method will return 3.| u | : The knot whose knot interval is seeked. |
 lies.
lies. Definition at line 123 of file vpBSpline.cpp.
References vpBSpline::findSpan().
|
inlineinherited |
Gets all the control points.
| list | : A std::list containing the coordinates of the control points. |
Definition at line 136 of file vpBSpline.h.
|
inlineinherited |
Gets all the crossing points (used in the interpolation method)
| list | : A std::list containing the coordinates of the crossing points. |
Definition at line 163 of file vpBSpline.h.
|
inlineinherited |
Gets all the knots.
| list | : A std::list containing the value of the knots. |
Definition at line 149 of file vpBSpline.h.
|
inlineinherited |
Gets the degree of the B-Spline.
Definition at line 128 of file vpBSpline.h.
|
inline |
Gets all the weights relative to the control points.
| list | [out] : A std::list containing weights relative to the control points. |
| void vpNurbs::globalCurveApprox | ( | const std::list< vpImagePoint > & | l_crossingPoints, |
| unsigned int | n | ||
| ) |
Method which enables to compute a NURBS curve approximating a set of data points.
The data points are approximated thanks to a least square method.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
| n | : The desired number of control points. The parameter n must be under or equal to the number of data points. |
Definition at line 725 of file vpNurbs.cpp.
References globalCurveApprox(), and weights.
| void vpNurbs::globalCurveApprox | ( | const std::list< vpMeSite > & | l_crossingPoints, |
| unsigned int | n | ||
| ) |
Method which enables to compute a NURBS curve approximating a set of data points.
The data points are approximated thanks to a least square method.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
| n | : The desired number of control points. This parameter n must be under or equal to the number of data points. |
Definition at line 734 of file vpNurbs.cpp.
References globalCurveApprox(), and weights.
|
static |
Method which enables to compute a NURBS curve approximating a set of data points.
The data points are approximated thanks to a least square method.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
| l_p | : Degree of the NURBS basis functions. |
| l_n | : The desired number of control points. l_n must be under or equal to the number of data points. |
| l_knots | : The knot vector. |
| l_controlPoints | : the list of control points. |
| l_weights | : the list of weights. |
Definition at line 592 of file vpNurbs.cpp.
References vpMatrix::AtA(), vpBSpline::computeBasisFuns(), vpBSpline::findSpan(), vpMatrix::pseudoInverse(), and vpImagePoint::set_ij().
Referenced by globalCurveApprox(), and vpMeNurbs::track().
| void vpNurbs::globalCurveApprox | ( | unsigned int | n | ) |
Method which enables to compute a NURBS curve approximating a set of data points.
The data points are approximated thanks to a least square method.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
Definition at line 744 of file vpNurbs.cpp.
References globalCurveApprox(), and weights.
Method which enables to compute a NURBS curve approximating a set of data points.
The data points are approximated thanks to a least square method.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
| n | : The desired number of control points. This parameter n must be under or equal to the number of data points. |
Definition at line 711 of file vpNurbs.cpp.
References vpList< type >::front(), vpMeSite::get_ifloat(), vpMeSite::get_jfloat(), globalCurveApprox(), vpList< type >::next(), vpList< type >::outside(), vpList< type >::value(), and weights.
| void vpNurbs::globalCurveInterp | ( | ) |
Method which enables to compute a NURBS curve passing through a set of data points.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
Definition at line 590 of file vpNurbs.cpp.
References weights.
Referenced by globalCurveInterp().
| void vpNurbs::globalCurveInterp | ( | const std::list< vpImagePoint > & | l_crossingPoints | ) |
Method which enables to compute a NURBS curve passing through a set of data points.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
Definition at line 561 of file vpNurbs.cpp.
References globalCurveInterp(), and weights.
| void vpNurbs::globalCurveInterp | ( | const std::list< vpMeSite > & | l_crossingPoints | ) |
Method which enables to compute a NURBS curve passing through a set of data points.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
Definition at line 571 of file vpNurbs.cpp.
References vpImagePoint::distance(), vpMeSite::get_ifloat(), vpMeSite::get_jfloat(), globalCurveInterp(), and weights.
|
static |
Method which enables to compute a NURBS curve passing through a set of data points.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
| l_p | : Degree of the NURBS basis functions. This value need to be > 0. |
| l_knots | : The knot vector. |
| l_controlPoints | : The list of control points. |
| l_weights | : the list of weights. |
Definition at line 463 of file vpNurbs.cpp.
References vpException::badValue, vpBSpline::computeBasisFuns(), vpBSpline::findSpan(), vpMatrix::pseudoInverse(), and vpImagePoint::set_ij().
Referenced by vpMeNurbs::initTracking().
Method which enables to compute a NURBS curve passing through a set of data points.
The result of the method is composed by a knot vector, a set of control points and a set of associated weights.
| l_crossingPoints | : The list of data points which have to be interpolated. |
Definition at line 540 of file vpNurbs.cpp.
References vpImagePoint::distance(), vpList< type >::front(), vpMeSite::get_ifloat(), vpMeSite::get_jfloat(), globalCurveInterp(), vpList< type >::next(), vpList< type >::outside(), vpImagePoint::set_ij(), vpList< type >::value(), and weights.
|
static |
Insert ![]() knots in the knot vector.
knots in the knot vector.
Of course the knot vector changes. But The list of control points and the list of the associated weights change too.
| l_x | : Several real numbers which are between the extremities of the knot vector and which have to be inserted. |
| l_r | : Number of knot in the array |
| l_p | : Degree of the NURBS basis functions. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
| l_weights | : the list of weights. |
Definition at line 250 of file vpNurbs.cpp.
References vpBSpline::findSpan(), and vpImagePoint::set_i().
Referenced by refineKnotVectCurve().
| void vpNurbs::refineKnotVectCurve | ( | double * | x, |
| unsigned int | r | ||
| ) |
Insert ![]() knots in the knot vector.
knots in the knot vector.
Of course the knot vector changes. But The list of control points and the list of the associated weights change too.
| x | : Several real numbers which are between the extremities of the knot vector and which have to be inserted. |
| r | : Number of knot in the array |
Definition at line 330 of file vpNurbs.cpp.
References refineKnotVectCurve(), and weights.
| unsigned int vpNurbs::removeCurveKnot | ( | double | l_u, |
| unsigned int | l_r, | ||
| unsigned int | l_num, | ||
| double | l_TOL | ||
| ) |
Remove ![]() times the knot
times the knot  from the knot vector. The removed knot
from the knot vector. The removed knot  is the
is the ![]() th vector in the knot vector.
th vector in the knot vector.
Of course the knot vector changes. But The list of control points and the list of the associated weights change too.
| l_u | : A real number which is between the extremities of the knot vector and which has to be removed. |
| l_r | : Index of |
| l_num | : Number of times |
| l_TOL | : A parameter which has to be computed. |
![]()
where ![]() is the minimal weight on the original curve,
is the minimal weight on the original curve, ![]() is the maximum distance of any point on the original curve from the origin and
is the maximum distance of any point on the original curve from the origin and ![]() is the desired bound on deviation.
is the desired bound on deviation.
Definition at line 458 of file vpNurbs.cpp.
References removeCurveKnot(), and weights.
|
static |
Remove ![]() times the knot
times the knot ![]() from the knot vector. The removed knot
from the knot vector. The removed knot ![]() is the
is the ![]() th vector in the knot vector.
th vector in the knot vector.
Of course the knot vector changes. But The list of control points and the list of the associated weights change too.
| l_u | : A real number which is between the extremities of the knot vector and which has to be removed. |
| l_r | : Index of |
| l_num | : Number of times |
| l_TOL | : A parameter which has to be computed. |
| l_s | : Multiplicity of |
| l_p | : Degree of the NURBS basis functions. |
| l_knots | : The knot vector |
| l_controlPoints | : the list of control points. |
| l_weights | : the list of weights. |
![]()
where ![]() is the minimal weight on the original curve,
is the minimal weight on the original curve, ![]() is the maximum distance of any point on the original curve from the origin and
is the maximum distance of any point on the original curve from the origin and ![]() is the desired bound on deviation.
is the desired bound on deviation.
Definition at line 335 of file vpNurbs.cpp.
References vpImagePoint::get_i(), vpImagePoint::get_j(), vpImagePoint::set_i(), vpImagePoint::set_j(), and vpMath::sqr().
Referenced by removeCurveKnot().
|
inlineinherited |
Sets all the control points.
| list | : A std::list containing the coordinates of the control points |
Definition at line 183 of file vpBSpline.h.
|
inlineinherited |
Sets all the crossing points (used in the interpolation method)
| list | : A std::list containing the coordinates of the crossing points |
Definition at line 210 of file vpBSpline.h.
|
inlineinherited |
Sets all the knots.
| list | : A std::list containing the value of the knots. |
Definition at line 196 of file vpBSpline.h.
|
inlineinherited |
Sets the degree of the B-Spline.
| degree | : the degree of the B-Spline. |
Definition at line 176 of file vpBSpline.h.
|
inline |
Sets all the knots.
| list | : A std::list containing the value of the knots. |
|
protected |
Vector which contains the weights associated to each control Points.
Definition at line 95 of file vpNurbs.h.
Referenced by computeCurveDers(), computeCurveDersPoint(), computeCurvePoint(), curveKnotIns(), globalCurveApprox(), globalCurveInterp(), refineKnotVectCurve(), and removeCurveKnot().