 |
Visual Servoing Platform
version 3.6.1 under development (2024-04-25)
|
 |
Visual Servoing Platform
version 3.6.1 under development (2024-04-25)
|
#include <visp3/core/vpMeterPixelConversion.h>
Static Public Member Functions | |
Using ViSP camera parameters <br> | |
| static void | convertEllipse (const vpCameraParameters &cam, const vpSphere &sphere, vpImagePoint ¢er_p, double &n20_p, double &n11_p, double &n02_p) |
| static void | convertEllipse (const vpCameraParameters &cam, const vpCircle &circle, vpImagePoint ¢er_p, double &n20_p, double &n11_p, double &n02_p) |
| static void | convertEllipse (const vpCameraParameters &cam, double xc_m, double yc_m, double n20_m, double n11_m, double n02_m, vpImagePoint ¢er_p, double &n20_p, double &n11_p, double &n02_p) |
| static void | convertLine (const vpCameraParameters &cam, const double &rho_m, const double &theta_m, double &rho_p, double &theta_p) |
| static void | convertPoint (const vpCameraParameters &cam, const double &x, const double &y, double &u, double &v) |
| static void | convertPoint (const vpCameraParameters &cam, const double &x, const double &y, vpImagePoint &iP) |
Using OpenCV camera parameters <br> | |
| static void | convertEllipse (const cv::Mat &cameraMatrix, const vpCircle &circle, vpImagePoint ¢er, double &n20_p, double &n11_p, double &n02_p) |
| static void | convertEllipse (const cv::Mat &cameraMatrix, const vpSphere &sphere, vpImagePoint ¢er, double &n20_p, double &n11_p, double &n02_p) |
| static void | convertEllipse (const cv::Mat &cameraMatrix, double xc_m, double yc_m, double n20_m, double n11_m, double n02_m, vpImagePoint ¢er_p, double &n20_p, double &n11_p, double &n02_p) |
| static void | convertLine (const cv::Mat &cameraMatrix, const double &rho_m, const double &theta_m, double &rho_p, double &theta_p) |
| static void | convertPoint (const cv::Mat &cameraMatrix, const cv::Mat &distCoeffs, const double &x, const double &y, double &u, double &v) |
| static void | convertPoint (const cv::Mat &cameraMatrix, const cv::Mat &distCoeffs, const double &x, const double &y, vpImagePoint &iP) |
Various conversion functions to transform primitives (2D ellipse, 2D line, 2D point) from normalized coordinates in meter in the image plane into pixel coordinates.
Transformation relies either on ViSP camera parameters implemented in vpCameraParameters or on OpenCV camera parameters that are set from a projection matrix and a distortion coefficients vector.
Definition at line 66 of file vpMeterPixelConversion.h.
|
static |
Noting that the perspective projection of a 3D circle is usually an ellipse, using the camera intrinsic parameters converts the parameters of the 3D circle expressed in the image plane (these parameters are obtained after perspective projection of the 3D circle) in the image with values in pixels using OpenCV camera parameters.
The ellipse resulting from the conversion is here represented by its parameters ![]() corresponding to its center coordinates in pixel and the centered moments normalized by its area.
corresponding to its center coordinates in pixel and the centered moments normalized by its area.
| [in] | cameraMatrix | : Camera Matrix |
| [in] | circle | : 3D circle with internal vector circle.p[] that contains the ellipse parameters expressed in the image plane. These parameters are internally updated after perspective projection of the sphere. |
| [out] | center | : Center of the corresponding ellipse in the image with coordinates expressed in pixels. |
| [out] | n20_p,n11_p,n02_p | : Second order centered moments of the ellipse normalized by its area (i.e., such that 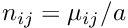 where where 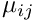 are the centered moments and a the area) expressed in pixels. are the centered moments and a the area) expressed in pixels. |
The following code shows how to use this function:
Definition at line 250 of file vpMeterPixelConversion.cpp.
References convertPoint(), vpTracker::p, and vpMath::sqr().
|
static |
Noting that the perspective projection of a 3D sphere is usually an ellipse, using the camera intrinsic parameters converts the parameters of the 3D sphere expressed in the image plane (these parameters are obtained after perspective projection of the 3D sphere) in the image with values in pixels using OpenCV camera parameters.
The ellipse resulting from the conversion is here represented by its parameters ![]() corresponding to its center coordinates in pixel and the centered moments normalized by its area.
corresponding to its center coordinates in pixel and the centered moments normalized by its area.
| [in] | cameraMatrix | : Camera Matrix |
| [in] | sphere | : 3D sphere with internal vector circle.p[] that contains the ellipse parameters expressed in the image plane. These parameters are internally updated after perspective projection of the sphere. |
| [out] | center | : Center of the corresponding ellipse in the image with coordinates expressed in pixels. |
| [out] | n20_p,n11_p,n02_p | : Second order centered moments of the ellipse normalized by its area (i.e., such that 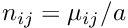 where where 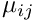 are the centered moments and a the area) expressed in pixels. are the centered moments and a the area) expressed in pixels. |
The following code shows how to use this function:
Definition at line 299 of file vpMeterPixelConversion.cpp.
References convertPoint(), vpTracker::p, and vpMath::sqr().
|
static |
Convert parameters of an ellipse expressed in the image plane (these parameters are obtained after perspective projection of the 3D sphere) in the image with values in pixels using ViSP intrinsic camera parameters.
The ellipse resulting from the conversion is here represented by its parameters ![]() corresponding to its center coordinates in pixel and the centered moments normalized by its area.
corresponding to its center coordinates in pixel and the centered moments normalized by its area.
| [in] | cameraMatrix | : Camera Matrix |
| [in] | xc_m,yc_m | : Center of the ellipse in the image plane with normalized coordinates expressed in meters. |
| [in] | n20_m,n11_m,n02_m | : Second order centered moments of the ellipse normalized by its area (i.e., such that 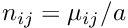 where where 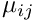 are the centered moments and a the area) expressed in meter. are the centered moments and a the area) expressed in meter. |
| [out] | center_p | : Center |
| [out] | n20_p,n11_p,n02_p | : Second order centered moments of the ellipse normalized by its area (i.e., such that 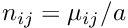 where where 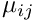 are the centered moments and a the area) expressed in pixels. are the centered moments and a the area) expressed in pixels. |
Definition at line 337 of file vpMeterPixelConversion.cpp.
References convertPoint(), and vpMath::sqr().
|
static |
Noting that the perspective projection of a 3D circle is usually an ellipse, using the camera intrinsic parameters converts the parameters of the 3D circle expressed in the image plane (these parameters are obtained after perspective projection of the 3D circle) in the image with values in pixels using ViSP camera parameters.
The ellipse resulting from the conversion is here represented by its parameters ![]() corresponding to its center coordinates in pixel and the centered moments normalized by its area.
corresponding to its center coordinates in pixel and the centered moments normalized by its area.
| [in] | cam | : Intrinsic camera parameters. |
| [in] | circle | : 3D circle with internal vector circle.p[] that contains the ellipse parameters expressed in the image plane. These parameters are internally updated after perspective projection of the sphere. |
| [out] | center_p | : Center |
| [out] | n20_p,n11_p,n02_p | : Second order centered moments of the ellipse normalized by its area (i.e., such that 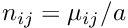 where where 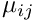 are the centered moments and a the area) expressed in pixels. are the centered moments and a the area) expressed in pixels. |
The following code shows how to use this function:
Definition at line 99 of file vpMeterPixelConversion.cpp.
References convertPoint(), vpCameraParameters::get_px(), vpCameraParameters::get_py(), vpTracker::p, and vpMath::sqr().
|
static |
Noting that the perspective projection of a 3D sphere is usually an ellipse, using the camera intrinsic parameters converts the parameters of the 3D sphere expressed in the image plane (these parameters are obtained after perspective projection of the 3D sphere) in the image with values in pixels.
The ellipse resulting from the conversion is here represented by its parameters ![]() corresponding to its center coordinates in pixel and the centered moments normalized by its area.
corresponding to its center coordinates in pixel and the centered moments normalized by its area.
| [in] | cam | : Intrinsic camera parameters. |
| [in] | sphere | : 3D sphere with internal vector circle.p[] that contains the ellipse parameters expressed in the image plane. These parameters are internally updated after perspective projection of the sphere. |
| [out] | center_p | : Center |
| [out] | n20_p,n11_p,n02_p | : Second order centered moments of the ellipse normalized by its area (i.e., such that 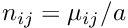 where where 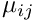 are the centered moments and a the area) expressed in pixels. are the centered moments and a the area) expressed in pixels. |
The following code shows how to use this function:
Definition at line 142 of file vpMeterPixelConversion.cpp.
References convertPoint(), vpCameraParameters::get_px(), vpCameraParameters::get_py(), vpTracker::p, and vpMath::sqr().
Referenced by vpFeatureDisplay::displayEllipse(), vpMbtDistanceCircle::getModelForDisplay(), vpMbtDistanceCircle::initMovingEdge(), and vpMbtDistanceCircle::updateMovingEdge().
|
static |
Convert parameters of an ellipse expressed in the image plane (these parameters are obtained after perspective projection of the 3D sphere) in the image with values in pixels using ViSP intrinsic camera parameters.
The ellipse resulting from the conversion is here represented by its parameters ![]() corresponding to its center coordinates in pixel and the centered moments normalized by its area.
corresponding to its center coordinates in pixel and the centered moments normalized by its area.
| [in] | cam | : Intrinsic camera parameters. |
| [in] | xc_m,yc_m | : Center of the ellipse in the image plane with normalized coordinates expressed in meters. |
| [in] | n20_m,n11_m,n02_m | : Second order centered moments of the ellipse normalized by its area (i.e., such that 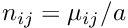 where where 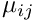 are the centered moments and a the area) expressed in meter. are the centered moments and a the area) expressed in meter. |
| [out] | center_p | : Center |
| [out] | n20_p,n11_p,n02_p | : Second order centered moments of the ellipse normalized by its area (i.e., such that 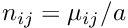 where where 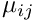 are the centered moments and a the area) expressed in pixels. are the centered moments and a the area) expressed in pixels. |
Definition at line 178 of file vpMeterPixelConversion.cpp.
References convertPoint(), vpCameraParameters::get_px(), vpCameraParameters::get_py(), and vpMath::sqr().
|
static |
Line parameters conversion from normalized coordinates ![]() expressed in the image plane to pixel coordinates
expressed in the image plane to pixel coordinates ![]() using OpenCV camera parameters. This function doesn't use distortion coefficients.
using OpenCV camera parameters. This function doesn't use distortion coefficients.
| [in] | cameraMatrix | : Camera Matrix |
| [in] | rho_p,theta_p | : Line parameters expressed in pixels. |
| [out] | rho_m,theta_m | : Line parameters expressed in meters in the image plane. |
Definition at line 200 of file vpMeterPixelConversion.cpp.
References vpException::divideByZeroError, vpMath::sqr(), and vpERROR_TRACE.
|
static |
Line parameters conversion from normalized coordinates ![]() expressed in the image plane to pixel coordinates
expressed in the image plane to pixel coordinates ![]() using ViSP camera parameters. This function doesn't use distortion coefficients.
using ViSP camera parameters. This function doesn't use distortion coefficients.
| [in] | cam | : camera parameters. |
| [in] | rho_p,theta_p | : Line parameters expressed in pixels. |
| [out] | rho_m,theta_m | : Line parameters expressed in meters in the image plane. |
Definition at line 56 of file vpMeterPixelConversion.cpp.
References vpException::divideByZeroError, vpMath::sqr(), and vpERROR_TRACE.
Referenced by vpFeatureDisplay::displayLine(), vpMbtDistanceKltCylinder::getModelForDisplay(), vpMbtDistanceCylinder::getModelForDisplay(), vpMbtDistanceCylinder::initMovingEdge(), vpMbtDistanceLine::initMovingEdge(), vpMbtDistanceCylinder::updateMovingEdge(), and vpMbtDistanceLine::updateMovingEdge().
|
static |
Point coordinates conversion from normalized coordinates 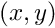 in meter in the image plane to pixel coordinates
in meter in the image plane to pixel coordinates 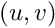 in the image using OpenCV camera parameters.
in the image using OpenCV camera parameters.
| [in] | cameraMatrix | : Camera Matrix |
| [in] | distCoeffs | : Input vector of distortion coefficients |
| [in] | x | : input coordinate in meter along image plane x-axis. |
| [in] | y | : input coordinate in meter along image plane y-axis. |
| [out] | u | : output coordinate in pixels along image horizontal axis. |
| [out] | v | : output coordinate in pixels along image vertical axis. |
Definition at line 367 of file vpMeterPixelConversion.cpp.
|
static |
Point coordinates conversion from normalized coordinates 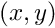 in meter in the image plane to pixel coordinates
in meter in the image plane to pixel coordinates 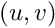 in the image using OpenCV camera parameters.
in the image using OpenCV camera parameters.
| [in] | cameraMatrix | : Camera Matrix |
| [in] | distCoeffs | : Input vector of distortion coefficients |
| [in] | x | : input coordinate in meter along image plane x-axis. |
| [in] | y | : input coordinate in meter along image plane y-axis. |
| [out] | iP | : output coordinates in pixels. |
Definition at line 393 of file vpMeterPixelConversion.cpp.
References vpImagePoint::set_u(), and vpImagePoint::set_v().
|
inlinestatic |
Point coordinates conversion from normalized coordinates 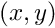 in meter in the image plane to pixel coordinates
in meter in the image plane to pixel coordinates 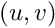 in the image using ViSP camera parameters.
in the image using ViSP camera parameters.
The used formula depends on the projection model of the camera. To know the currently used projection model use vpCameraParameter::get_projModel()
| [in] | cam | : camera parameters. |
| [in] | x | : input coordinate in meter along image plane x-axis. |
| [in] | y | : input coordinate in meter along image plane y-axis. |
| [out] | u | : output coordinate in pixels along image horizontal axis. |
| [out] | v | : output coordinate in pixels along image vertical axis. |
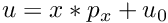 and
and 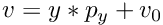 in the case of perspective projection without distortion.
in the case of perspective projection without distortion.
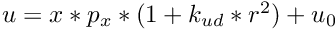 and
and 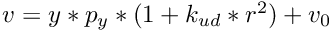 with
with 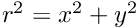 in the case of perspective projection with distortion.
in the case of perspective projection with distortion.
In the case of a projection with Kannala-Brandt distortion, refer to [22].
Definition at line 105 of file vpMeterPixelConversion.h.
References vpCameraParameters::perspectiveProjWithDistortion, vpCameraParameters::perspectiveProjWithoutDistortion, and vpCameraParameters::ProjWithKannalaBrandtDistortion.
Referenced by vpPolygon::buildFrom(), vpPose::computeResidual(), vpMbtFaceDepthNormal::computeROI(), vpMbtFaceDepthDense::computeROI(), convertEllipse(), vpFeatureBuilder::create(), vpFeatureSegment::display(), vpProjectionDisplay::display(), vpProjectionDisplay::displayCamera(), vpMbtFaceDepthNormal::displayFeature(), vpPose::displayModel(), vpFeatureDisplay::displayPoint(), vpImageDraw::drawFrame(), vpMbtFaceDepthNormal::getFeaturesForDisplay(), vpMbtDistanceKltPoints::getModelForDisplay(), vpMbtDistanceLine::getModelForDisplay(), vpPolygon3D::getNbCornerInsideImage(), vpPolygon3D::getRoi(), vpPolygon3D::getRoiClipped(), vpMbtDistanceLine::initMovingEdge(), vpKeyPoint::matchPointAndDetect(), vpWireFrameSimulator::projectCameraTrajectory(), vpSimulatorAfma6::updateArticularPosition(), vpSimulatorViper850::updateArticularPosition(), vpMbtDistanceLine::updateMovingEdge(), and vpKinect::warpRGBFrame().
|
inlinestatic |
Point coordinates conversion from normalized coordinates 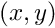 in meter in the image plane to pixel coordinates in the image using ViSP camera parameters.
in meter in the image plane to pixel coordinates in the image using ViSP camera parameters.
The used formula depends on the projection model of the camera. To know the currently used projection model use vpCameraParameter::get_projModel()
| [in] | cam | : camera parameters. |
| [in] | x | : input coordinate in meter along image plane x-axis. |
| [in] | y | : input coordinate in meter along image plane y-axis. |
| [out] | iP | : output coordinates in pixels. |
In the frame (u,v) the result is given by:
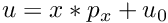 and
and 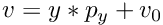 in the case of perspective projection without distortion.
in the case of perspective projection without distortion.
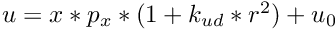 and
and 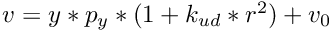 with
with 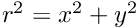 in the case of perspective projection with distortion.
in the case of perspective projection with distortion.
In the case of a projection with Kannala-Brandt distortion, refer to [22].
Definition at line 147 of file vpMeterPixelConversion.h.
References vpCameraParameters::perspectiveProjWithDistortion, vpCameraParameters::perspectiveProjWithoutDistortion, and vpCameraParameters::ProjWithKannalaBrandtDistortion.